11. Container With Most Water/盛最多水的容器

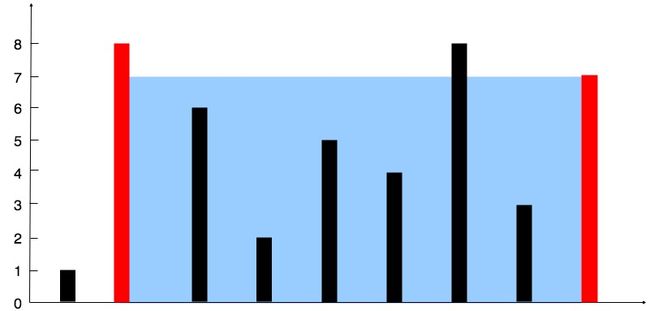
Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example:

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

AC代码

class Solution {
public:
    int maxArea(vector& height) {
        int ans = 0, tmp = 0;
        for (int i = 0; i < height.size(); ++i)
            for (int j = i + 1; j < height.size(); j++) {
                tmp = (j - i) * min(height[i], height[j]);
                if (tmp > ans) ans = tmp;
            }
        return ans;
    }
};

O(n)代码

class Solution {
public:
    int maxArea(vector& height) {
        int left = 0, right = height.size() - 1, ans = 0;
        while (left < right) {
            ans = max(ans, min(height[left], height[right]) * (right - left));
            if (height[left] < height[right]) left++;
            else right--;
        }
        return ans;
    }
};

总结

尽管知道O(n²)肯定不是最优解，但一时半会儿确实没想起优化方法，O(n)算法参考资料:
https://segmentfault.com/a/1190000008824222