梯度下降算法原理 线性回归拟合（附Python/Matlab/Julia代码）

梯度下降

梯度下降法的原理

  梯度下降法(gradient descent)是一种常用的一阶(first-order)优化方法，是求解无约束优化问题最简单、最经典的方法之一。

  梯度下降最典型的例子就是从山上往下走，每次都寻找当前位置最陡峭的方向小碎步往下走，最终就会到达山下（暂不考虑有山谷的情况）。

  首先来解释什么是梯度？这就要先讲微分。对于微分，相信大家都不陌生，看几个例子就更加熟悉了。

先来看单变量的微分：
$$\frac{d\left(x^2\right)}{dx}=2x$$

再看多变量的微分：

$$\begin{gathered} \frac{\partial }{\partial x}\left(x^{2}y\right)=2xy \\ \frac{\partial }{\partial y}\left(x^{2}y\right)=x^2 \end{gathered}$$

补充:导数和微分的区别
  导数是函数在某一点处的斜率，是Δy和Δx的比值；而微分是指函数在某一点处的切线在横坐标取得增量Δx以后，纵坐标取得的增量，一般表示为dy。

  梯度就是由微分结果组成的向量，令

$$f(x,y,z)=x^2+2xy+3yz$$
有
$$\{\begin{array}{c}\frac{\partial f}{\partial x}=2x+2y\\ \\ \frac{\partial f}{\partial y}=2x+3z\\ \\ \frac{\partial f}{\partial z}=3y\end{array}$$

那么，函数f(x,y,z)在(1,2,3)处的微分为

$$\{\begin{array}{c}\frac{\partial f}{\partial x}=2x+2y=2\ast 1+2\ast 2=6\\ \\ \frac{\partial f}{\partial y}=2x+3z=2\ast 1+3\ast 3=11\\ \\ \frac{\partial f}{\partial z}=3y=3\ast 2=6\end{array}$$
因此，函数f(x,y,z)在(1,2,3)处的梯度为(6,11,6)。

  梯度是一个向量，对于一元函数，梯度就是该点处的导数，表示切线的斜率。对于多元函数，梯度的方向就是函数在该点上升最快的方向。

  梯度下降法就是每次都寻找梯度的反方向，这样就能到达局部的最低点。

  那为什么按照梯度的反方向能到达局部的最低点呢？这个问题直观上很容易看出来，但严禁起见，我们还是给出数学证明。

对于连续可微函数f(x)，从某个随机点出发，想找到局部最低点，可以通过构造一个序列$x_0,x_1,x_2...$,能够满足

$$f(x_{t+1})<f(x_t),t=0,1,2...$$
那么我们就能够不断执行该过程即可收敛到局部极小点，可参考下图。

  那么问题就是如何找到下一个点$x^{t+1}$ ,并保证$f(x^{t+1})<f(x^t)$ 呢？我们以一元函数为例来说明。对于一元函数来说，x是会存在两个方向：要么是正方向 ($\Delta x>0$ )，要么是负方向（$\Delta x<0$ ），如何选择每一步的方向，就需要用到大名鼎鼎的泰勒公式，先看一下下面这个泰勒展式：

$$f(x+\Delta x)\simeq f(x)+\Delta x\nabla f(x)$$

其中$\nabla f(x)$表示f(x)在x处的导数。

若想$f(x+\Delta x)<f(x)$,就需要保证$\Delta x\nabla f(x)<0$，令

$$\Delta x=-\alpha \nabla f(x),(\alpha >0)$$
步长$\alpha$是一个较小的正数，从而有
$$\Delta x\nabla f(x)=-\alpha (\nabla f(x){)}^2<0$$

因此，有
$$f(x+\Delta x)=f(x-\alpha \nabla f(x))\simeq f(x)-\alpha (\nabla f(x){)}^2<f(x)$$

每一步我们都按照$x_{i+1}=x_i-\alpha \nabla f(x)$更新x，这就是梯度下降的原理。

  这里再对$\alpha$解释一下，α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离。既要保证步子不能太小，还没下到山底太阳就下山了；也要保证步子不能跨的太大，可能会导致错过最低点。

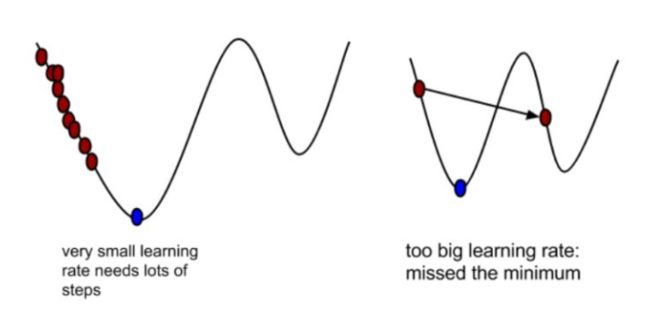
  在梯度前加负号就是朝梯度的反方向前进，因为梯度是上升最快的方向，所以方向就是下降最快的方向。

梯度下降的实例

一元函数的梯度下降

  设一元函数为
$$J(\theta )={\theta }^2$$

函数的微分为
$$J^{\prime }(\theta )=2\theta$$

设起点为${\theta }_0=1$，步长$\alpha =0.4$,根据梯度下降的公式
${\theta }_1={\theta }_0-\alpha \nabla J(\theta )$,经过4次迭代：
$$\begin{gathered} {\theta }_0=1 \\ {\theta }_1={\theta }_0-0.4\ast 2\ast 1=0.2 \\ {\theta }_2={\theta }_1-0.4\ast 2\ast 0.2=0.04 \\ {\theta }_3={\theta }_2-0.4\ast 2\ast 0.04=0.008 \end{gathered}$$

多元函数的梯度下降

设二元函数为
$$J(\Theta )={\theta }_1^2+{\theta }_2^2$$

函数的梯度为

$$\nabla J(\Theta )=(2{\theta }_1,2{\theta }_2)$$

设起点为(2,3)，步长$\alpha =0.1$,根据梯度下降的公式,经过多次迭代后，有

$$\begin{gathered} {\Theta }_0=(2,3) \\ {\Theta }_1={\Theta }_0-0.1\ast (2\ast 2,2\ast 3)=(1.6,2.4) \\ {\Theta }_2={\Theta }_1-0.1\ast (2\ast 1.6,2\ast 2.4)=(1.28,1.92) \\ ⋮ \\ {\Theta }_{99}={\Theta }_{98}-0.1\ast {\Theta }_{98}=(6.36e-10,9.55e-10) \\ {\Theta }_{100}={\Theta }_{99}-0.1\ast {\Theta }_{99}=(5.09e-10,7.64e-10) \end{gathered}$$

loss function(损失函数)

  损失函数也叫代价函数(cost function)，是用来衡量模型预测出来的值h(θ)与真实值y之间的差异的函数，如果有多个样本，则可以将所有代价函数的取值求均值，记做J(θ)。代价函数有下面几个性质：

1. 对于每种算法来说，代价函数不是唯一的；
2. 代价函数是参数θ的函数；
3. 总的代价函数J(θ)可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本(x, y)；
4. J(θ)是一个标量。

  最常见的代价函数是均方误差函数，即

$$J\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}\sum _{i=1}^m{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$
其中，

• m为训练样本的个数

• $h_{\theta }(x)$表示估计值，表达式如下
  $$h_{\Theta }\left(x^{(i)}\right)={\Theta }_0+{\Theta }_1{x}_1^{(i)}$$

• y是原训练样本中的值

  我们需要做的就是找到θ的值，使得J(θ)最小。代价函数的图形跟我们上面画过的图很像，如下图所示。

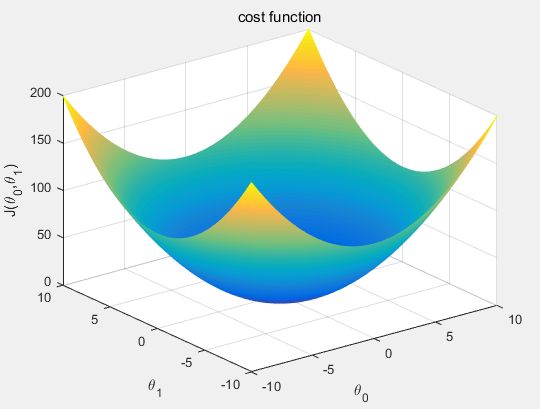
  看到这个图，相信大家也就知道了我们可以用梯度下降算法来求可以使代价函数最小的θ值。

先求代价函数的梯度

$$\begin{array}{c}\nabla J(\Theta )=⟨\frac{\partial J}{\partial {\Theta }_0},\frac{\partial J}{\partial {\Theta }_1}⟩\\ \\ \frac{\partial J}{\partial {\Theta }_0}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\Theta }\left(x^{(i)}\right)-y^{(i)}\right)\\ \\ \frac{\partial J}{\partial {\Theta }_1}=\frac{1}{m}{\sum }_{i=1}^m\left(h_{\Theta }\left(x^{(i)}\right)-y^{(i)}\right)x_1^{(i)}\end{array}$$

  这里有两个变量${\theta }_0$和${\theta }_1$，为了方便矩阵表示，我们给x增加一维，这一维的值都是1，并将会乘到${\theta }_0$上。那么cost function的矩阵形式为：

$$\begin{array}{c}J(\Theta )=\frac{1}{2m}(X\Theta -y{)}^T(X\Theta -y)\\ \\ \nabla J(\Theta )=\frac{1}{m}{X}^T(X\Theta -y)\end{array}$$

  这么看公式可能很多同学会不太明白，我们把每个矩阵的具体内容表示出来，大家就很容易理解了。

矩阵$\Theta$为：
$$\left[\begin{array}{l}{\theta }_0\\ \\ {\theta }_1\end{array}\right]$$

矩阵X为：

$$\left[\begin{array}{ccc}1& & x^0\\ 1& & x^1\\ 1& & x^2\\ & ⋮& \\ 1& & x^m\end{array}\right]$$

矩阵y为:
$$\left[\begin{array}{c}{y}^0\\ y^1\\ ⋮\\ y^m\end{array}\right]$$

这样写出来后再去对应上面的公式，就很容易理解了。

  下面我们来举一个用梯度下降算法来实现线性回归的例子。有一组数据如下图所示，我们尝试用求出这些点的线性回归模型。

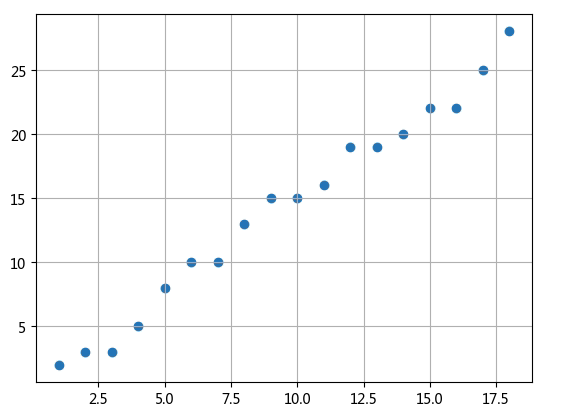
首先产生矩阵X和矩阵y

# generate matrix X
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))

# matrix y
y = np.array([2,3,3,5,8,10,10,13,15,15,16,19,19,20,22,22,25,28]).reshape(m,1)

按照上面的公式定义梯度函数

def gradient_function(theta, X, y):
	diff = np.dot(X, theta) - y
	return (1./m) * np.dot(np.transpose(X), diff)

接下来就是最重要的梯度下降算法，我们取${\theta }_0$和${\theta }_1$的初始值都为1，再进行梯度下降过程。

def gradient_descent(X, y, alpha):
	theta = np.array([1, 1]).reshape(2, 1)
	gradient = gradient_function(theta, X, y)
	while not np.all(np.absolute(gradient) <= 1e-5):
		theta = theta - alpha * gradient
		gradient = gradient_function(theta, X, y)
	return theta

通过该过程，最终求出的${\theta }_0=0.137$，${\theta }_1=1.477$，线性回归的曲线如下

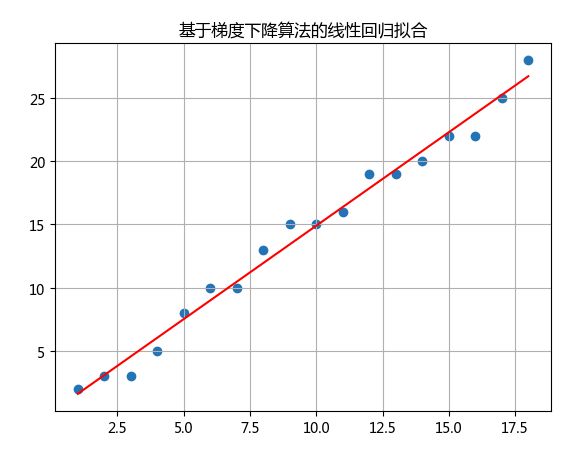
附录 source code

matlab一元函数的梯度下降程序

clc;
close all;
clear all;
%% 
delta = 1/100000;
x = -1.1:delta:1.1;
y = x.^2;
dot = [1, 0.2, 0.04, 0.008];
figure;plot(x,y);
axis([-1.2, 1.2, -0.2, 1.3]);
grid on
hold on
plot(dot, dot.^2,'r');
for i=1:length(dot)
    text(dot(i),dot(i)^2,['\theta_{',num2str(i),'}']);
end
title('一元函数的梯度下降过程');

python一元函数的梯度下降程序

import numpy as np 
import matplotlib.pyplot as plt

delta = 1/100000
x = np.arange(-1.1, 1.1, delta)
y = x ** 2
dot = np.array([1, 0.2, 0.04, 0.008])
plt.figure(figsize=(7,5))
plt.plot(x,y)
plt.grid(True)
plt.xlim(-1.2, 1.2)
plt.ylim(-0.2, 1.3)
plt.plot(dot, dot**2, 'r')
for i in range(len(dot)):
    plt.text(dot[i],dot[i]**2,r'$\theta_%d$' % i)
plt.title('一元函数的梯度下降过程')
plt.show()

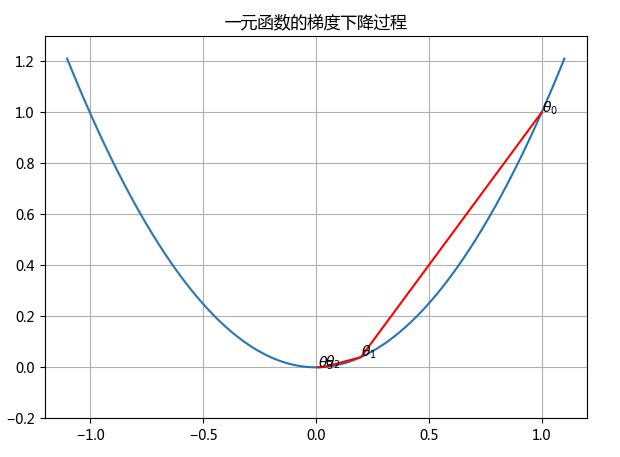
julia一元函数的梯度下降程序

using PyPlot
delta = 1/100000
x = -1.1:delta:1.1
y = x.^2
dot = [1, 0.2, 0.04, 0.008]
plot(x, y)
grid(true)
axis("tight")
plot(dot, dot.^2, color="r")
for i=1:length(dot)
    text(dot[i], dot[i]^2, "\$\\theta_$i\$")
end
title("Single variable function gradient descent")

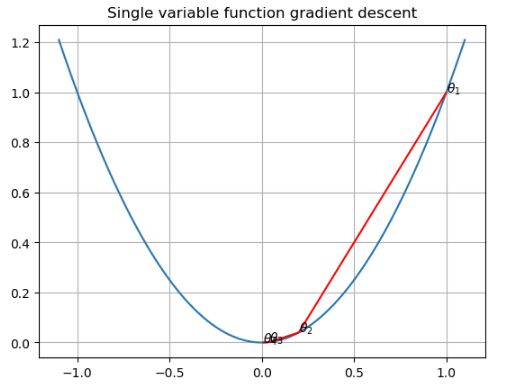
matlab二元函数的梯度下降程序

pecision = 1/100;
[x,y] = meshgrid(-3.1:pecision:3.1);
z = x.^2 + y.^2;
figure;
mesh(x,y,z);
dot = [[2,3];[1.6,2.4];[1.28,1.92];[5.09e-10, 7.64e-10]];
hold on
scatter3(dot(:,1),dot(:,2),dot(:,1).^2+dot(:,2).^2,'r*');
for i=1:4
   text(dot(i,1)+0.4,dot(i,2),dot(i,1).^2+0.2+dot(i,2).^2+0.2,['\theta_{',num2str(i),'}']);
end
title('二元函数的梯度下降过程')

python二元函数的梯度下降程序

import numpy as np 
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x = np.linspace(-3.1,3.1,300)
y = np.linspace(-3.1,3.1,300)
x,y = np.meshgrid(x, y)
z = x**2 + y**2
dot = np.array([[2,3],[1.6,2.4],[1.28,1.92],[5.09e-10, 7.64e-10]])
fig = plt.figure(figsize = (10,6))
ax = fig.gca(projection = '3d')
cm = plt.cm.get_cmap('YlGnBu')
surf = ax.plot_surface(x, y, z, cmap=cm)
fig.colorbar(surf,shrink=0.5, aspect=5)
ax.scatter3D(dot[:,0], dot[:,1], dot[:,0]**2 + dot[:,1]**2, marker='H',c='r')
for i in range(len(dot)-1):
    ax.text(dot[i,0]+0.4, dot[i,1], dot[i,0]**2 + dot[i,1]**2, r'$\Theta_%d$' % i)
ax.text(dot[3,0]+0.4, dot[3,1]+0.4, dot[3,0]**2 + dot[3,1]**2-0.4, r'min')
plt.show()

julia二元函数的梯度下降程序

这个图的text死活标不上，希望知道的朋友可以告知一下。再多说一句，虽然我之前出了个Julia的教程，里面也包含4种绘图工具(Plots,GR,Gadfly & PyPlot)，但没有画过3维的图形，今天为了画这个图可真是费尽周折，Julia官网上的3D绘图的程序基本没有一个可以直接使用的，具体的绘图过程和调试中碰到的问题我还会整理篇文章到知乎和公众号，大家可以看一下。

using Plots
Plots.plotlyjs()
n = 50
x = range(-3, stop=3, length=n)
y= x
z = zeros(n,n)
for i in 1:n, k in 1:n
    z[i,k] = x[i]^2 + y[k]^2
end

surface(x, y, z)
dot = [[2 3]; [1.6 2.4]; [1.28 1.92]; [5.09e-10  7.64e-10]]
scatter!(dot[:,1], dot[:,2], dot[:,1].^2 .+ dot[:,2].^2)

matlab梯度下降的线性回归

m = 18;
X0 = ones(m,1);
X1 = (1:m)';
X = [X0, X1];
y = [2,3,3,5,8,10,10,13,15,15,16,19,19,20,22,22,25,28]';
alpha = 0.01;
theta = gradient_descent(X, y, alpha, m);

function [grad_res] =  gradient_function(theta, X, y, m)
    diff = X * theta - y;
    grad_res = X' * diff / m;
end

function [theta_res] =  gradient_descent(X, y, alpha, m)
    theta = [1;1];
    gradient = gradient_function(theta, X, y, m);
    while sum(abs(gradient)>1e-5)>=1
        theta = theta - alpha * gradient;
        gradient = gradient_function(theta, X, y, m);
    end
    theta_res = theta;
end

python梯度下降的线性回归

import numpy as np 
import matplotlib.pyplot as plt 

# y = np.array([2,3,3,5,8,10,10,13,15,15,16,19,19,20,22,22,25,28])
# x = np.arange(1,len(y)+1)
# plt.figure()
# plt.scatter(x,y)
# plt.grid(True)
# plt.show()

# sample length
m = 18

# generate matrix X
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))

# matrix y
y = np.array([2,3,3,5,8,10,10,13,15,15,16,19,19,20,22,22,25,28]).reshape(m,1)

# alpha
alpha = 0.01

def cost_function(theta, X, y):
	diff = np.dot(X, theta) - y
	return (1./2*m) * np.dot(np.transpose(diff), diff)

def gradient_function(theta, X, y):
	diff = np.dot(X, theta) - y
	return (1./m) * np.dot(np.transpose(X), diff)

def gradient_descent(X, y, alpha):
	theta = np.array([1, 1]).reshape(2, 1)
	gradient = gradient_function(theta, X, y)
	while not np.all(np.absolute(gradient) <= 1e-5):
		theta = theta - alpha * gradient
		gradient = gradient_function(theta, X, y)
	return theta

[theta0, theta1] = gradient_descent(X, y, alpha)
plt.figure()
plt.scatter(X1,y)
plt.plot(X1, theta0 + theta1*X1, color='r')
plt.title('基于梯度下降算法的线性回归拟合')
plt.grid(True)
plt.show()

julia梯度下降的线性回归

m = 18
X0 = ones(m,1)
X1 = Array(1:m)
X = [X0 X1];
y = [2,3,3,5,8,10,10,13,15,15,16,19,19,20,22,22,25,28];
alpha = 0.01;
theta = gradient_descent(X, y, alpha, m)

function gradient_function(theta, X, y, m)
    diff = X * theta .- y;
    grad_res = X' * diff / m;
end

function gradient_descent(X, y, alpha, m)
    theta = [1,1]
    gradient = gradient_function(theta, X, y, m)
    while all(abs.(gradient) .>1e-5)==true
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y, m)
    end
    theta_res = theta
end