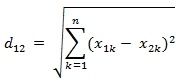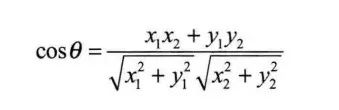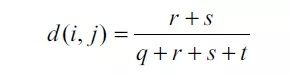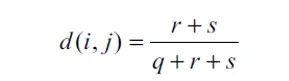R-数据挖掘 | 聚类分析中的各种相异(似)度计算
目录
一、聚类的基本数据结构
二、不同数据类型的相异度计算方法
(一)区间标度变量
(二)二元变量
(三)标称变量
(四)顺序变量
(五)比例标度型变量
(六)混合类型
三、R相异(似)度计算总结
一、聚类的基本数据结构
假设要聚类的数据集合包含 n 个数据对象,这些数据对象可能表示人,房子,文档,国家等。许多基于内存的聚类算法选择如下两种有代表性的数据结构:
(1)数据矩阵(Data matrix,或称对象-属性结构)
用 p 个变量(也称为属性)来表现 n 个对象,例如用年龄,身高,性别,种族等属性来表现对象“人”。这种数据结构是关系表的形式,或者看为 n*p 维( n 个对象*p 个属性)的矩阵。
(2)相异度矩阵(dissimilarity matrix 或称对象-对象结构)
存储 n 个对象两两之间的近似性,表现形式是一个 n*n 维的矩阵。在这里 d(i,j)是对象 i 和对象 j 之间相异性的量化表示,通常它是一个非负的数值,当对象 i 和j 越相似,其值越接近 0;两个对象越不同,其值越大。既然 d(i,j) = d(j,i),而且 d(i,i)=0,我们可以得到如下的矩阵。
数据矩阵经常被称为二模( two-mode)矩阵,而相异度矩阵被称为单模( one-mode)矩阵。这是因为前者的行和列代表不同的实体,而后者的行和列代表相同的实体。许多聚类算法以相异度矩阵为基础。如果数据是用数据矩阵的形式表现的,在使用该类算法之前要将其转化为相异度矩阵。
二、不同数据类型的相异度计算方法
聚类算法的基本出发点在于根据对象间相似度将对象划分为不同的类。对于n个数据对象,其可能具有m个属性变量,其中,属性变量可能是区间标度变量、二元变量、 标称变量、序数型变量、比例标度变量等等,对于不同类型的属性变量以及由各种类型变量组成的混合类型变量的相似度计算,需要采用特定的方法。
(一)区间标度变量
基本呈直线比例的连续变量。典型的例子包括重量和高度、大气温度等。对于这类变量。通常度量标准有两种:距离和相似性系数。
1、距离法
距离是指:把一个观测看做M维空间中的一个点,并在空间中定义距离。基于距离的聚类算法是把距离较近的点可以归入同一类,距离远的点归入不同的类。常见的距离度量方法有欧几里得距离、切比雪夫距离、曼哈顿距离、兰氏距离等方法。
(1)欧几里得距离
其意义就是两个元素在欧氏空间中的集合距离,因为其直观易懂且可解释性强,被广泛用于标识两个标量元素的相异度。
-
二维平面上点a(x1,y1)与b(x2,y2)间的欧氏距离:
-
三维空间点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:
-
n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离(两个n维向量):
用R语言计算距离主要是dist函数。若X是一个M×N的矩阵,则dist(X)将X矩阵M行的每一行作为一个N维向量,然后计算这M个向量两两间的距离。
a=matrix(rnorm(15,0,1),c(3,5))
a
[,1] [,2] [,3] [,4] [,5]
[1,] -1.3687632 -0.1256902 1.831776 0.04040039 0.7215346
[2,] -0.9527400 0.1411766 1.869298 0.48506072 -0.4510057
[3,] -0.5019286 -0.5775474 -0.266830 -1.25701475 0.6687304
dist(a,p=2)
1 2
2 1.348434
3 2.654392 3.093780第一个行与第二行的距离为1.348434;第二行与第三行的距离为3.093780;第一行与第三行的距离为2.654392。
(2)标准化的欧几里得距离
引入标准化欧式距离的原因是各个维度之间的尺度不一样。例如如果向量中第一维元素的数量级是100,第二维的数量级是10,比如v1=(100,10,30),v2 = (500,40),则计算欧式距离:
欧式距离会给第一维度100权重,这会压制第二维度的影响力,影响聚类效果。因此需要对所有维度分别进行处理,而标准化欧式距离即是将集合X={xi} 先进行归一化,映射到正太分布N(0,1)的区间。两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式为:
其中Sk是分量的标准差。
(3)切比雪夫距离
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
-
二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离:
![]()
-
n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离:
-
R语言实现
a=matrix(rnorm(15,0,1),c(3,5))
a
[,1] [,2] [,3] [,4] [,5]
[1,] 0.4862698 1.60416329 2.1782714 -0.0482251 0.07532716
[2,] -0.9037107 -0.02123885 1.2375462 0.5486704 1.05818544
[3,] 2.2151023 0.46779567 -0.8486798 -0.1302249 1.10995354
dist(aa,"maximum")
1 2
2 1.172540
3 2.098606 2.136128(4)曼哈顿距离
顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
-
二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离:
![]()
-
n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离:
-
R语言实现
aa=matrix(rnorm(15,0,1),c(3,5))
aa
[,1] [,2] [,3] [,4] [,5]
[1,] 1.70799453 -0.04141924 0.07297395 0.9798695 -1.216628
[2,] 0.03756585 -1.19296077 -0.92721255 0.3491397 -1.747676
[3,] 0.81945921 1.77140128 0.03894016 0.4126954 1.983640
dist(aa,"manhattan")
1 2
2 4.983935
3 6.502832 8.507280(5)兰氏距离
兰氏距离对数据的量纲不敏感。不过兰氏距离假定变量之间相互独立,没有考虑变量之间的相关性。
-
R语言实现
aa=matrix(rnorm(15,0,1),c(3,5))
aa
[,1] [,2] [,3] [,4] [,5]
[1,] 1.6333474 -0.5834216 -0.9462516 0.2086602 -0.3769740
[2,] 0.9626742 -0.1751355 -0.5063374 0.8873260 -0.3339518
[3,] -0.6620339 1.1891228 0.7396146 1.3988866 -0.5574114
dist(aa, method = "canberra")
1 2
2 1.779179
3 14.381702 12.565129(6)闵科夫斯基距离(明氏距离)
闵可夫斯基距离不是一种距离,而是一组距离的定义。两个n维变量a(a1;a2;...;an)与b(b1;b2;...;bn)间的闵可夫斯基距离的定义为:
其中p为一个变参数
- 当p=1时,就是曼哈顿距离;
- 当p=2时,就是欧式距离;
- 当p→∞时,就是切比雪夫距离;
-
R语言实现
aa=matrix(rnorm(15,0,1),c(3,5))
aa
[,1] [,2] [,3] [,4] [,5]
[1,] -0.04438065 -0.2507179 -0.8686347 0.33079315 0.1945877
[2,] -2.75157088 0.3174601 0.2447662 0.15134978 0.4980498
[3,] -0.38604912 -0.3735566 -0.3158024 0.02866034 -0.9828699
dist(aa,"minkowski",p=2)
1 2
2 3.002608
3 1.383886 2.931827(7)马氏距离
马氏距离表示数据的协方差距离,优点是量纲无关,考虑到变量(特性)之间的相关性,缺点是:不同的特征不能差别对待,可能夸大弱特征。
马氏距离最典型的应用是根据距离做判别,假设有n个总体,计算某个样品X归属于哪一类。此时虽然样品X离某个总体的欧氏距离最近,但是未必归属它,比如该总体的方差很小,说明需要非常近才能归为该类。对于这种情况,马氏距离比欧氏距离更适合作判别。
-
R语言实现
mashi <-function(a,b)
+ {
+ #a,b均为向量
+ return (((a-b)%*% t(t(a-b))) / cov(a,b))
+ }
a=rnorm(5,0,1)
b=rnorm(5,1,1)
a
[1] -0.3838747 1.3189950 1.5704322 0.7796178 1.6880347
b
[1] -0.2906927 1.9139708 1.3061692 2.6417586 -0.2719465
mashi(a,b)
[,1]
[1,] 30.44869 2、相似性系数
(1)夹角余弦(Cosine)
a. 在二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式:
b. N维样本点A(x11,x12,…,x1n)与B(x21,x22,…,x2n)的夹角余弦:
即:
要注意,余弦度量的不是两者的相异度,而是相似度!cosθ余弦值的取值范围[-1,1].夹角余弦越大,表示两个向量的夹角越小,越相似;夹角余弦越小,表示两个向量之间的夹角越大,越不相似。
-
R语言实现
aa=matrix(rnorm(15,0,1),c(3,5))
aa
[,1] [,2] [,3] [,4] [,5]
[1,] -1.1598850 -0.9505939 -0.1636752 0.3253987 -0.6856397
[2,] 1.5563910 -0.1753408 -0.5399991 1.2201594 0.9428927
[3,] 0.3078279 -0.1812549 -1.8798527 -0.8432773 0.8025968
bb <- matrix(rep(0,9),3,3)
bb
[,1] [,2] [,3]
[1,] 0 0 0
[2,] 0 0 0
[3,] 0 0 0
for (i in 1:3)
+ for (j in 1:3)
+ if (i < j)
+ bb[i,j] = sum(t(aa[i,])*aa[j,])/sqrt((sum(aa[i,]^2))*sum(aa[j,]^2))
bb
[,1] [,2] [,3]
[1,] 0 -0.4708508 -0.1855322
[2,] 0 0.0000000 0.2473352
[3,] 0 0.0000000 0.0000000(2)修正的余弦相似性
→ 为什么需要在余弦相似度的基础上使用修正余弦相似度
X和Y两个用户对两个内容的评分分别为(1,2)和(4,5),使用余弦相似度得到的结果是0.98,两者极为相似。但从评分上看X似乎不喜欢2这个 内容,而Y则比较喜欢,余弦相似度对数值的不敏感导致了结果的误差,需要修正这种不合理性
修正cosine相似度的目的是解决cosine相似度仅考虑向量维度方向上的相似而没考虑到各个维度的量纲的差异性,所以在计算相似度的时候,做了每个维度减去均值的修正操作。
(3)皮尔森相关系数
R语言实现:
aa=matrix(rnorm(15,0,1),c(3,5))
aa
[,1] [,2] [,3] [,4] [,5]
[1,] 0.5755751 -0.3297866 0.2265403 -1.4046601 0.05077459
[2,] -0.0272368 -1.0808926 1.2412669 -0.7370180 0.62487326
[3,] -1.0533600 -0.9267481 0.5732794 -0.2181805 0.36626637
1-cor(t(aa))
[,1] [,2] [,3]
[1,] 0.0000000 0.4167359 1.0302624
[2,] 0.4167359 0.0000000 0.2385867
[3,] 1.0302624 0.2385867 0.0000000(二)二元变量
只有两个状态(0或1)的变量称为二元变量。二元变量分为对称的和非对称的两种。如果假设所有的二元变量有相同的权重,则可以得到一个两行两列(2*2)的条件表。
q表示在对象i和对象j中均取1的二值变量个数; r表示在对象i取1但对象j中取0的二值变量个数; s表示在对象i中取0而在对象j中取1的二值变量个数; t则表示在对象i和对象j中均取0的二值变量个数。 二值变量的总数为p,则:p=q+r+s+t。
1. 对称的二元变量
两个状态是同等价值的,具有同样的权重,例如属性“性别”,有两个值“女性”和“男性”,两个取值都没有优先权。这类变量通常用简单匹配系数计算:
其中,中r为i和j取值不相同的属性的个数;s为i 和j取值相同的属性的个数。
2. 不对称的二元变量
两个状态具有不同权重。如一个疾病disease的测试结果positive或negative,显然这两个测试结果的重要性是不一样的。对于非对称的二元变量之间相似度的度量最著名的有Jaccard系数:
-
R语言实现
x <- matrix(sample(c(FALSE, TRUE), 8, rep = TRUE), ncol = 2)
x
[,1] [,2]
[1,] TRUE TRUE
[2,] FALSE FALSE
[3,] TRUE TRUE
[4,] TRUE FALSE
dist(x, method = "Jaccard")
1 2 3
2 1.0
3 0.0 1.0
4 0.5 1.0 0.5(三)标称变量
标称变量是二元变量的推广,可具有多于两个的状态值,如颜色变量(红、橙、黄、绿、蓝等)。两个对象 i 和 j 之间的相异性可以根据不匹配率来计算:
其中,m是匹配的数目(即对象 i 和 j 取值相同的属性数),而p是刻画对象的属性总数,我们可以通过赋予m较大的权重来增加m的影响。
例如,包含标称属性的表,只有一个标称属性,p值等于1,设置m值为1:
(四)顺序变量
顺序变量类似于标称变量,不过序数型变量的各个状态是以有意义的序列排序的。通常,可以将序数型变量的值映射为秩。计算两个对象i和j相异度的时候,用相应的秩代替实际取值,并标准化到[0,1]区间,之后利用距离度量方法进行计算。
假设f是用于描述n个对象的一组顺序变量之一,关于f的相异度计算如下:
接下来就可以用区间标度变量中所描述的任意一组距离度量方法进行计算相异度。
(五)比例标度型变量
比例标度型变量在非线性的标度上取正的度量值,例如指数标度:
在计算比例数值变量所描述对象间的距离时,有两种处理方法:
1)将比例数值变量看作区间标度变量,采用相同的方法处理,但不佳,因为比例尺度是非线性的;
2)采用对数变换
对比例数值变量进行处理,然后将Yif当做区间标度变量来处理。
(六)混合类型
在实际数据库中,数据对象往往是用复合数据类型来描述的,而且常常包括以上六种数据类型:区间标度变量、对称二元变量、不对称二元变量、符号类型、顺序类型和比例数值类型。
1)一种方法是将变量按类型分组,对每种类型的变量单独聚类分析,如果分析得对兼容的结果,这种方法可行,但实际中,往往不可行。
2) 一种更可取的方法是将所有的变量一起处理,只进行一次聚类分析。
一种技术是将不同类型的变量组合在单个相异度矩阵中,把所有有意义的变量转换到共同的值域区间[0,1]上。假设数据集包含p个不同类型的变量,对象i和j间的相异度d(i,j)定义为:
变量f对i和j直接相异度的计算方式与其具体类型有关:
三、R相异(似)度计算总结
使用R计算距离时,常用的函数是stats包中dist()和 cluster包中的daisy(),dist()用于计算区间标度属性的相异性矩阵,而daisy()函数用于计算二元属性、标称属性、顺序属性、比例属性和混合属性的相异性矩阵。
1、使用dist()函数计算相异性矩阵
stats包中的dist()函数用于计算两个数值型观测值之间的距离:
dist(x, method = "euclidean", diag = FALSE, upper = FALSE, p = 2)
该函数计算并返回通过使用指定的距离度量计算的距离矩阵,以计算数据矩阵的行之间的距离。
参数注释:
x:矩阵、数据框或dist对象
method:度量距离的方法,默认值是"euclidean",可用的方法是:"euclidean"、"maximum"、"manhattan"、"canberra"、"binary" 和"minkowski",中文名称分别是:欧几里得、最大距离、曼哈顿、兰氏距离、二元距离和闵科夫斯基距离。
diag:逻辑值,是否绘制距离矩阵的对角线(diagonal)
upper:逻辑值,是否绘制距离矩阵的上三角(upper triangle)
p:用于闵科夫斯基距离,指定power值
dist()方法返回一个下三角矩阵,使用as.matrix()函数可以使用标准中括号得到距离。
2、使用daisy()函数计算相异性矩阵
cluster包中的daisy()函数用于计算数据集中两个观测值之间的距离。当原始变量是混合类型,或者设置metric="gower"时,daisy()都会使用Gower公式计算数据集的相异型矩阵。
daisy(x, metric = c("euclidean", "manhattan", "gower"),stand = FALSE, type = list(), weights = rep.int(1, p), ...)
x:数值矩阵或数据框,数值类型的变量被识别为区间缩放变量,因子类型的变量被识别为标称属性,有序因子被识别为有序变量,其他变量类型需要在type参数中指定。
metric:字符类型,有效值是 "euclidean" (默认值)、 "manhattan" 和 "gower"。
stand:逻辑值,在计算相异性之前是否按列对数据进行标准化
type:list类型,用于指定x中变量的类型,有效的列表项是"ordratio" (用于序数变量),、"logratio" (用于对数转换)、"asymm" (用于非对称二元属性) 和"symm" (用于对称二元属性和标称属性)
weights:数值向量(长度是x的列的数量 p=ncol(x)),用于混合类型的变量(或 metric="gower"),指定每个变量的权重,默认的权重是1。
函数描述:
daisy()通过使用Gower相异系数(1971)来实现对标称、序数和二元属性数据的处理。如果x的变量是标称、序数和二元类型的数据,那么函数将忽略metric和stand参数,使用Gower 系数计算数据矩阵的距离。对于纯数值数据,也可以通过设置metric="gower"来计算相异性矩阵,计算的流程是先对数据对象进行标准化,标准化的算法是:(x-min)/(max-min),把数据缩放到范围[0.0, 1.0]中。
[ Reference ]
1. 各种类型的数据的相异度(相似度)的度量:https://blog.csdn.net/u010451580/article/details/53163634
2. 机器学习 第二篇:基于距离评估数据的相似性和相异性:https://www.cnblogs.com/ljhdo/archive/2018/08/24/4876877.html
3. 机器学习——几种距离度量方法比较:
https://my.oschina.net/hunglish/blog/787596
4. R语言计算各种距离:
https://blog.csdn.net/xxzhangx/article/details/53153821