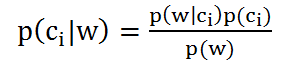文章原创,最近更新:2018-08-20
学习参考链接:第4章 基于概率论的分类方法:朴素贝叶斯
本章节的主要内容是:
重点介绍项目案例1:屏蔽社区留言板的侮辱性言论:训练算法:从词向量计算概率的代码。
1.朴素贝叶斯项目案例介绍:
项目案例1:
屏蔽社区留言板的侮辱性言论
项目概述:
构建一个快速过滤器来屏蔽在线社区留言板上的侮辱性言论。如果某条留言使用了负面或者侮辱性的语言,那么就将该留言标识为内容不当。对此问题建立两个类别: 侮辱类和非侮辱类,使用 1 和 0 分别表示。
朴素贝叶斯 工作原理:
提取所有文档中的词条并进行去重
获取文档的所有类别
计算每个类别中的文档数目
对每篇训练文档:
对每个类别:
如果词条出现在文档中-->增加该词条的计数值(for循环或者矩阵相加)
增加所有词条的计数值(此类别下词条总数)
对每个类别:
对每个词条:
将该词条的数目除以总词条数目得到的条件概率(P(词条|类别))
返回该文档属于每个类别的条件概率(P(类别|文档的所有词条))
开发流程:
- 收集数据: 可以使用任何方法
- 准备数据: 从文本中构建词向量
- 分析数据: 检查词条确保解析的正确性
- 训练算法: 从词向量计算概率
- 测试算法: 根据现实情况修改分类器
- 使用算法: 对社区留言板言论进行分类
数据集介绍
这个数据集是我们自己构造的词表.
2.训练算法:从词向量计算概率
2.1测试算法:分类器未修改前
def trainNB0(trainMatrix, trainCategory):
"""
训练数据原版
:param trainMatrix: 文件单词矩阵 [[1,0,1,1,1....],[],[]...]
:param trainCategory: 文件对应的标签类别[0,1,1,0....],列表长度等于单词矩阵数,其中的1代表对应的文件是侮辱性文件,0代表不是侮辱性矩阵
:return:
p0Vect: 各单词在分类0的条件下出现的概率
p1Vect: 各单词在分类1的条件下出现的概率
pAbusive: 文档属于分类1的概率
"""
# 文件数
numTrainDocs = len(trainMatrix)
# 单词数
numWords = len(trainMatrix[0])
# 侮辱性文件的出现概率,即trainCategory中所有的1的个数
# 代表的就是多少个侮辱性文件,与文件的总数相除就得到了侮辱性文件的出现概率
pAbusive = sum(trainCategory) / float(numTrainDocs)
p0Num = np.zeros(numWords); p1Num =np.zeros(numWords)
p1Num = np.zeros(numWords); p1Num =np.zeros(numWords)
#整个数据集单词出现总数
p0Denom = 0.0
p1Denom = 0.0
for i in range(numTrainDocs):
if trainCategory[i]==1:
p1Num += trainMatrix[i] #[0,1,1,....] + [0,1,1,....]->[0,2,2,...]
# 对向量中的所有元素进行求和,也就是计算所有侮辱性文件中出现的单词总数
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
# 类别1,即侮辱性文档的[P(F1|C1),P(F2|C1),P(F3|C1),P(F4|C1),P(F5|C1)....]列表
# 即 在1类别下,每个单词出现的概率
p1Vect = p1Num / p1Denom# [1,2,3,5]/90->[1/90,...]
# 类别0,即正常文档的[P(F1|C0),P(F2|C0),P(F3|C0),P(F4|C0),P(F5|C0)....]列表
# 即 在0类别下,每个单词出现的概率
p0Vect = p0Num / p0Denom
return p0Vect, p1Vect, pAbusive
测试代码及其结果如下:
import bayes
listOPosts,listClasses =loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat =[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V,P1V,PAb=bayes.trainNB0(trainMat, listClasses)
p0V
Out[93]:
array([ 0.04166667, 0.04166667, 0.04166667, 0.04166667, 0.125 ,
0.04166667, 0. , 0. , 0.04166667, 0. ,
0.04166667, 0.04166667, 0.04166667, 0. , 0. ,
0. , 0.04166667, 0.08333333, 0.04166667, 0. ,
0.04166667, 0.04166667, 0.04166667, 0.04166667, 0.04166667,
0. , 0. , 0.04166667, 0. , 0. ,
0.04166667, 0.04166667])
P1V
Out[94]:
array([ 0. , 0. , 0. , 0. , 0. ,
0. , 0.10526316, 0.05263158, 0. , 0.15789474,
0. , 0. , 0. , 0.05263158, 0.05263158,
0.05263158, 0. , 0.05263158, 0. , 0.05263158,
0.10526316, 0. , 0.05263158, 0.05263158, 0. ,
0.05263158, 0.05263158, 0. , 0.05263158, 0.05263158,
0. , 0. ])
PAb
Out[95]: 0.5
2.2测试算法:根据现实情况修改分类器
对于此公式:上一步做的工作仅仅是将各个分量求出来了(p(w)为1),而没有进行p(w0|ci) * p(w1|ci) * p(w2|ci) * .... * p(wn|ci)的累乘,也没有进行概率大小的比较。
剩下的工作看似简单但在具体实现上也涉及到两个问题。
问题一:p(wn|ci) 中有一个为0,导致整个累乘结果也为0。这是错误的结论。
解决方法:将所有词的出现次数初始化为1,并将分母初始化为2。问题二:即使 p(wn|ci) 不为0了,可是它的值也许会很小,这样会导致浮点数值类型的下溢出等精度问题错误。
解决方法:用 p(wn|ci) 的对数进行计算。
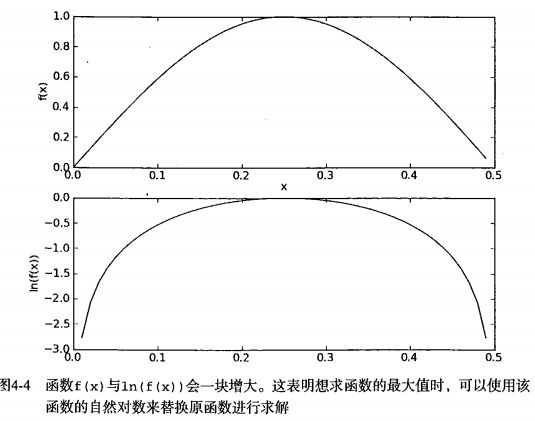
下图给出了函数 f(x) 与 ln(f(x)) 的曲线。可以看出,它们在相同区域内同时增加或者减少,并且在相同点上取到极值。它们的取值虽然不同,但不影响最终结果。
具体实现请参考下面代码。针对这两个问题,它对上一步的函数做了一点修改:
2.2.1修改的地方如下:
更改1
#更改前
p0Denom = 0.0
p1Denom = 0.0
#更改后
p0Denom = 2.0
p1Denom = 2.0
更改2
#更改前
p0Num = np.zeros(numWords); p1Num =np.zeros(numWords)
p1Num = np.zeros(numWords); p1Num =np.zeros(numWords)
#更改后
p0Num = np.ones(numWords); p1Num =np.zeros(numWords)
p1Num = np.ones(numWords); p1Num =np.zeros(numWords)
更改3
#更改前
p1Vect = p1Num / p1Denom # [1,2,3,5]/90->[1/90,...]
p0Vect = p0Num / p0Denom
#更改后
from math import log
p1Vect = log(p1Num / p1Denom)
p0Vect = log(p0Num / p0Denom)
2.2.2修改后,完整的代码如下:
def trainNB0(trainMatrix, trainCategory):
"""
训练数据原版
:param trainMatrix: 文件单词矩阵 [[1,0,1,1,1....],[],[]...]
:param trainCategory: 文件对应的标签类别[0,1,1,0....],列表长度等于单词矩阵数,其中的1代表对应的文件是侮辱性文件,0代表不是侮辱性矩阵
:return:
p0Vect: 各单词在分类0的条件下出现的概率
p1Vect: 各单词在分类1的条件下出现的概率
pAbusive: 文档属于分类1的概率
"""
# 总文件数
numTrainDocs = len(trainMatrix)
# 每个文件中的单词数
numWords = len(trainMatrix[0])
# 侮辱性文件的出现概率,即trainCategory中所有的1的个数
# 代表的就是多少个侮辱性文件,与文件的总数相除就得到了侮辱性文件的出现概率
pAbusive = sum(trainCategory) / float(numTrainDocs)
# p0Num 正常的统计,p1Num 侮辱的统计
p0Num = np.ones(numWords); p1Num =np.ones(numWords)
# 整个数据集单词出现总数,2.0根据样本/实际调查结果调整分母的值(2主要是避免分母为0,当然值可以调整)
# p0Num 正常的统计
# p1Num 侮辱的统计
p0Denom = 2.0
p1Denom = 2.0
for i in range(numTrainDocs):
if trainCategory[i]==1:
# 累加辱骂词的频次
p1Num += trainMatrix[i]
# 对每篇文章的辱骂的频次 进行统计汇总
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
# 类别1,即侮辱性文档的[log(P(F1|C1)),log(P(F2|C1)),log(P(F3|C1)),log(P(F4|C1)),log(P(F5|C1))....]列表
# log下什么都不写默认是自然对数
p1Vect = np.log(p1Num/p1Denom)
# 类别0,即正常文档的[log(P(F1|C0)),log(P(F2|C0)),log(P(F3|C0)),log(P(F4|C0)),log(P(F5|C0))....]列表
p0Vect = np.log(p0Num/p0Denom)
return p0Vect, p1Vect, pAbusive
测试代码及其结果如下:
import bayes
listOPosts,listClasses =loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat =[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V,P1V,PAb=bayes.trainNB0(trainMat, listClasses)
p0V
Out[173]:
array([-2.56494936, -2.56494936, -2.56494936, -2.56494936, -1.87180218,
-2.56494936, -3.25809654, -3.25809654, -2.56494936, -3.25809654,
-2.56494936, -2.56494936, -2.56494936, -3.25809654, -3.25809654,
-3.25809654, -2.56494936, -2.15948425, -2.56494936, -3.25809654,
-2.56494936, -2.56494936, -2.56494936, -2.56494936, -2.56494936,
-3.25809654, -3.25809654, -2.56494936, -3.25809654, -3.25809654,
-2.56494936, -2.56494936])
P1V
Out[174]:
array([-3.04452244, -3.04452244, -3.04452244, -3.04452244, -3.04452244,
-3.04452244, -1.94591015, -2.35137526, -3.04452244, -1.65822808,
-3.04452244, -3.04452244, -3.04452244, -2.35137526, -2.35137526,
-2.35137526, -3.04452244, -2.35137526, -3.04452244, -2.35137526,
-1.94591015, -3.04452244, -2.35137526, -2.35137526, -3.04452244,
-2.35137526, -2.35137526, -3.04452244, -2.35137526, -2.35137526,
-3.04452244, -3.04452244])
PAb
Out[175]: 0.5
2.2.3小案例模拟以上代码
import bayes
listOPosts,listClasses =loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat =[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V,P1V,PAb=bayes.trainNB0(trainMat, listClasses)
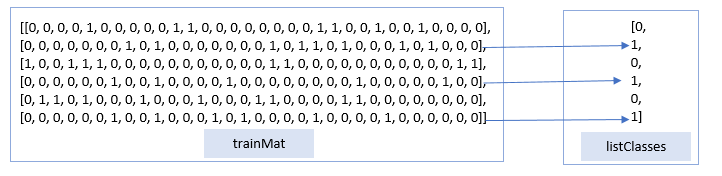
首先来看看输入的数据trainMat长什么样子.
Out[103]:trainMat
再看看输入的数据listClasses长什么样子.
listClasses
Out[106]: [0, 1, 0, 1, 0, 1]
再看看其他数据是长什么样子的
numTrainDocs = len(trainMat)
numWords = len(trainMat[0])
numTrainDocs
Out[108]: 6
numWords
Out[109]: 32
sum(listClasses)
Out[110]: 3
float(numTrainDocs)
Out[111]: 6.0
pAbusive = sum(listClasses) / float(numTrainDocs)
pAbusive
Out[114]: 0.5
p0Num = np.ones(numWords); p1Num =np.ones(numWords)
p0Num
Out[116]:
array([ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1.])
p1Num
Out[117]:
array([ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1.])
p0Denom = 2.0
p1Denom = 2.0
for i in range(numTrainDocs):
if listClasses[i]==1:
p1Num += trainMat[i]
p1Denom += sum(trainMat[i])
else:
p0Num += trainMat[i]
p0Denom += sum(trainMat[i])
p1Num
Out[122]:
array([ 1., 1., 1., 1., 1., 1., 3., 2., 1., 4., 1., 1., 1.,
2., 2., 2., 1., 2., 1., 2., 3., 1., 2., 2., 1., 2.,
2., 1., 2., 2., 1., 1.])
p1Denom
Out[123]: 21.0
p0Num
Out[124]:
array([ 2., 2., 2., 2., 4., 2., 1., 1., 2., 1., 2., 2., 2.,
1., 1., 1., 2., 3., 2., 1., 2., 2., 2., 2., 2., 1.,
1., 2., 1., 1., 2., 2.])
p0Denom
Out[125]: 26.0
p0V
Out[126]:
array([-2.56494936, -2.56494936, -2.56494936, -2.56494936, -1.87180218,
-2.56494936, -3.25809654, -3.25809654, -2.56494936, -3.25809654,
-2.56494936, -2.56494936, -2.56494936, -3.25809654, -3.25809654,
-3.25809654, -2.56494936, -2.15948425, -2.56494936, -3.25809654,
-2.56494936, -2.56494936, -2.56494936, -2.56494936, -2.56494936,
-3.25809654, -3.25809654, -2.56494936, -3.25809654, -3.25809654,
-2.56494936, -2.56494936])
P1V
Out[127]:
array([-3.04452244, -3.04452244, -3.04452244, -3.04452244, -3.04452244,
-3.04452244, -1.94591015, -2.35137526, -3.04452244, -1.65822808,
-3.04452244, -3.04452244, -3.04452244, -2.35137526, -2.35137526,
-2.35137526, -3.04452244, -2.35137526, -3.04452244, -2.35137526,
-1.94591015, -3.04452244, -2.35137526, -2.35137526, -3.04452244,
-2.35137526, -2.35137526, -3.04452244, -2.35137526, -2.35137526,
-3.04452244, -3.04452244])
PAb
Out[128]: 0.5
p1Num/p1Denom
Out[129]:
array([ 0.04761905, 0.04761905, 0.04761905, 0.04761905, 0.04761905,
0.04761905, 0.14285714, 0.0952381 , 0.04761905, 0.19047619,
0.04761905, 0.04761905, 0.04761905, 0.0952381 , 0.0952381 ,
0.0952381 , 0.04761905, 0.0952381 , 0.04761905, 0.0952381 ,
0.14285714, 0.04761905, 0.0952381 , 0.0952381 , 0.04761905,
0.0952381 , 0.0952381 , 0.04761905, 0.0952381 , 0.0952381 ,
0.04761905, 0.04761905])
p0Num/p0Denom
Out[130]:
array([ 0.07692308, 0.07692308, 0.07692308, 0.07692308, 0.15384615,
0.07692308, 0.03846154, 0.03846154, 0.07692308, 0.03846154,
0.07692308, 0.07692308, 0.07692308, 0.03846154, 0.03846154,
0.03846154, 0.07692308, 0.11538462, 0.07692308, 0.03846154,
0.07692308, 0.07692308, 0.07692308, 0.07692308, 0.07692308,
0.03846154, 0.03846154, 0.07692308, 0.03846154, 0.03846154,
0.07692308, 0.07692308])
p1Vect = np.log(p1Num/p1Denom)
p1Vect
Out[131]:
array([-3.04452244, -3.04452244, -3.04452244, -3.04452244, -3.04452244,
-3.04452244, -1.94591015, -2.35137526, -3.04452244, -1.65822808,
-3.04452244, -3.04452244, -3.04452244, -2.35137526, -2.35137526,
-2.35137526, -3.04452244, -2.35137526, -3.04452244, -2.35137526,
-1.94591015, -3.04452244, -2.35137526, -2.35137526, -3.04452244,
-2.35137526, -2.35137526, -3.04452244, -2.35137526, -2.35137526,
-3.04452244, -3.04452244])
p0Vect = np.log(p0Num/p0Denom)
p0Vect
Out[132]:
array([-2.56494936, -2.56494936, -2.56494936, -2.56494936, -1.87180218,
-2.56494936, -3.25809654, -3.25809654, -2.56494936, -3.25809654,
-2.56494936, -2.56494936, -2.56494936, -3.25809654, -3.25809654,
-3.25809654, -2.56494936, -2.15948425, -2.56494936, -3.25809654,
-2.56494936, -2.56494936, -2.56494936, -2.56494936, -2.56494936,
-3.25809654, -3.25809654, -2.56494936, -3.25809654, -3.25809654,
-2.56494936, -2.56494936])
2.2.4用数学公式演示2.2.1未改善前的代码
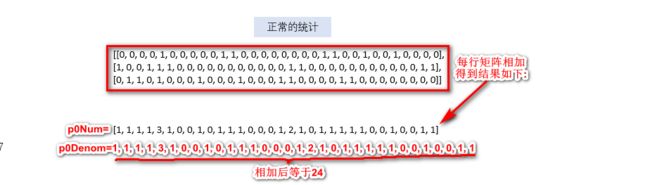
由此可以分别
得到正常的言论与侮辱的言论数据集,如下:
由此可以分别
得到相加后正常的言论与侮辱的言论数据集,如下:
由此可以得到P0V,P1V的值,具体如下:
P1V= p1Num / p1Denom,P0V=p0Num / p0Denom
3.相关知识点
知识点1:numpy.log(math.log)
学习参考链接:numpy.log(math.log)
- 以10为底:np.log10(x)
import numpy as np
np.log10(100)
Out[166]: 2.0
- e为底 :log下什么都不写默认是自然对数
np.log(np.e)
Out[167]: 1.0
np.log(10)
Out[168]: 2.3025850929940459
- 2为底:直接将2写在前面即可
np.log2(4)