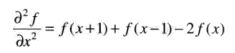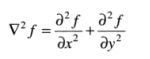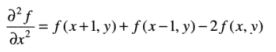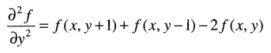数字图像处理-第三章-灰度变换与空间滤波
综述
对于图像的处理有两种思路，一种是对图像本身的直接处理，即空间域处理；另一种是在频率域进行处理。
在空间域的处理相对简单，因此首先介绍的是空域处理法。空域中有两种重要处理方法：灰度变换（或亮度变换,主要以对比度和阈值处理为目的）和空间滤波（或邻域处理、空间卷积,涉及改善性能的操作）。
---------------------------------------------------------------------------------------------------------------------------------------------------------------------
空间域处理：灰度变换和空间滤波
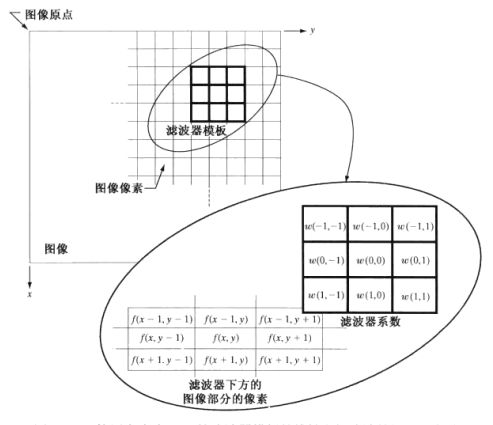
g(x,y)=T[ f(x,y) ]
空域处理的思路可以由上式表达。f 即是原图，T 是在点(x,y)指定邻域上的图像处理算子，g 是输出图像。
当邻域为1*1大小时，T 为灰度变换算子；邻域大于1*1时，T 为空间滤波算子。
- 灰度变换可以考虑每一个像素的灰度（点处理），也可以考虑整体灰度后再处理一个个像素（直方图处理）。
- 空间滤波是每次考虑一块像素，进行卷积操作。
首先介绍的是直接进行点处理的函数，这些函数来自MATLAB图像处理工具箱。之后会介绍直方图处理、空间滤波。
---------------------------------------------------------------------------------------------------------------------------------------------------------------------
灰度变换(点处理)
灰度变换可以看作领域大小为1*1的空间域处理，这这种情况下上式变为灰度变换函数：
s=T(r)
其中r和s分别是输入输出灰度
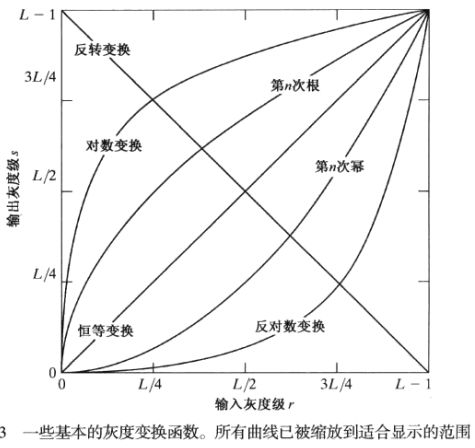
1-常见的灰度变换函数
常用的基本函数有三类：线性函数，对数函数（对数和反对数）和幂律函数（n次幂和n次根）
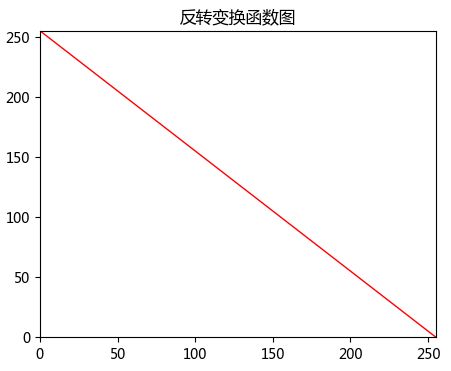
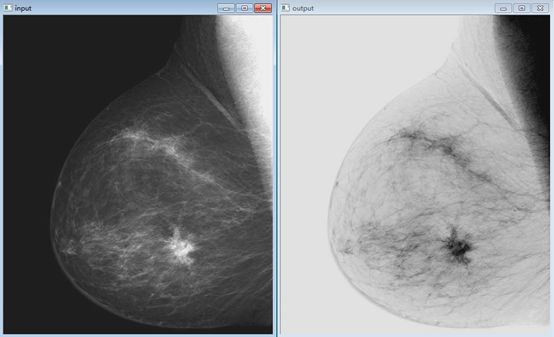
2-图像反转_增白增亮
适用于增强嵌入在一幅图像暗区域中的白色或灰色细节。变换公式为：
s=L-1-r
图像灰度级范围为[0,L-1]
"""反转变换"""
import numpy as np
import cv2
import matplotlib.pyplot as plt
def reverse(img):
output = 255 - img
return output
img1 = cv2.imread(r'F:\program_study\Python\data\breast.tif') # 前头加r是消除反斜杠转义
cv2.imshow('input', img1)
x = np.arange(0, 256, 0.01)
y = 255 - x
plt.plot(x, y, 'r', linewidth=1)
plt.title('反转变换函数图')
plt.xlim([0, 255]), plt.ylim([0, 255])
plt.show()
img_output = reverse(img1)
cv2.namedWindow('output', cv2.WINDOW_NORMAL) # 可改变窗口大小
cv2.imshow('output', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()3-对数变换_观察频谱(压缩值域)
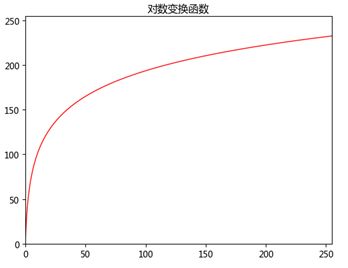
对数变换可以拉伸范围较窄的低灰度值，同时压缩范围较宽的高灰度值。可以用来扩展图像中的暗像素值，同时压缩亮像素值。
s=clog(1+r)
其中c为常数,r+1可以使得函数向左移一个单位,得到的s均大于0
一个典型的应用是傅立叶频谱（幅度谱）的显示。对傅立叶频谱进行对数变化，下面的上图中蓝线为变换函数，注意x轴量级为10的7次方，直接被压缩到了0-17.5，效果非常明显。下面的下图是经过对数变换，又经过最大最小值变换后的频谱.
(如果没有经过对数变换[或者说压缩],则该定义域对应的值域范围会非常大,下图显示的只会一个中央的亮点,参考冈萨雷斯P66的例子,这也是观察傅里叶变换前需要进行log处理的原因)
一般的对数变换
"""对数变换"""
import numpy as np
import matplotlib.pyplot as plt
import cv2
def log_plot(c):
x = np.arange(0, 256, 0.01)
y = c*np.log(1 + x)
plt.plot(x, y, 'r', linewidth=1)
plt.title('对数变换函数')
plt.xlim(0, 255), plt.ylim(0, 255)
plt.show()
def log(c, img):
output_img = c*np.log(1.0+img)
output_img = np.uint8(output_img+0.5)
return output_img
img_input = cv2.imread('F:\program_study\Python\data\pollens.tif')
cv2.imshow('input', img_input)
log_plot(42)
img_output = log(42, img_input)
cv2.imshow('output', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()
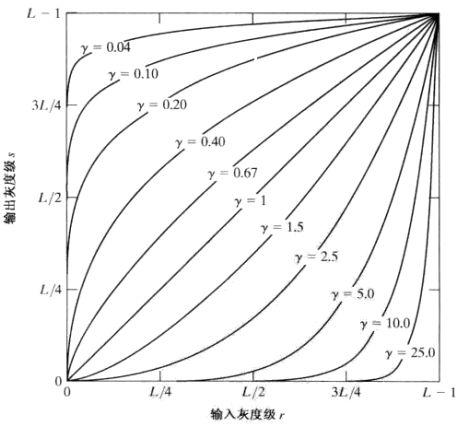
'''对数变换'''4-幂律(伽马)变换_增黑增暗(压缩灰度级)_增强对比度(扩展灰度级)
变换的基本形式为:
c和gamma为正常数
对于不同的gamma值,有不同的曲线
多用在图像整体偏暗，扩展灰度级。另外一种情况是，图像有“冲淡”的外观（很亮白）需要压缩中高以下的大部分的灰度级。
"""幂律变换（伽马）"""
import numpy as np
import matplotlib.pyplot as plt
import cv2
def gamma_plot(c, v):
x = np.arange(0, 256, 0.01)
y = c*x**v
plt.plot(x, y, 'r', linewidth=1)
plt.title('伽马变换函数')
plt.xlim([0, 255]), plt.ylim([0, 255])
plt.show()
def gamma(img, c, v):
lut = np.zeros(256, dtype=np.float32)
for i in range(256):
lut[i] = c * i ** v
output_img = cv2.LUT(img, lut)
output_img = np.uint8(output_img+0.5) # 这句一定要加上
return output_img
img_input = cv2.imread('F:\program_study\Python\data\city.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('imput', img_input)
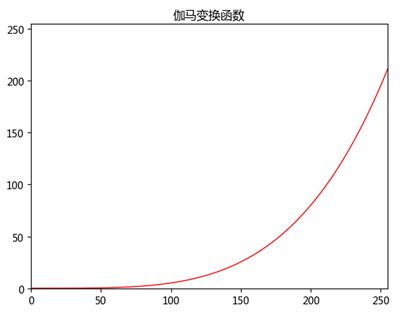
gamma_plot(0.00000005, 4.0)
img_output = gamma(img_input, 0.00000005, 4.0)
cv2.imshow('output', img_output)
cv2.waitKey(0)
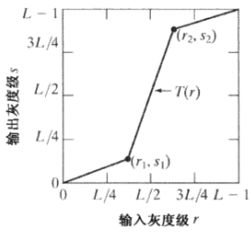
cv2.destroyAllWindows()6-分段线性变换
- 对比度拉伸(扩展图像灰度级动态范围)
"""分段线性变换Segmental Linear Transformation"""
import cv2
import numpy as np
import matplotlib.pyplot as plt
def SLT(img, x1, x2, y1, y2):
lut = np.zeros(256)
for i in range(256):
if i < x1:
lut[i] = (y1/x1)*i
elif i < x2:
lut[i] = ((y2-y1)/(x2-x1))*(i-x1)+y1
else:
lut[i] = ((y2-255.0)/(x2-255.0))*(i-255.0)+255.0
img_output = cv2.LUT(img, lut)
img_output = np.uint8(img_output+0.5)
return img_output
def SLT_plot(x1, x2, y1, y2):
plt.plot([0, x1, x2, 255], [0, y1, y2, 255], 'b', linewidth=1)
plt.plot([x1, x1, 0], [0, y1, y1], 'r--')
plt.plot([x2, x2, 0], [0, y2, y2], 'r--')
plt.title('分段线性变换函数')
plt.xlim([0, 255]), plt.ylim([0, 255])
plt.show()
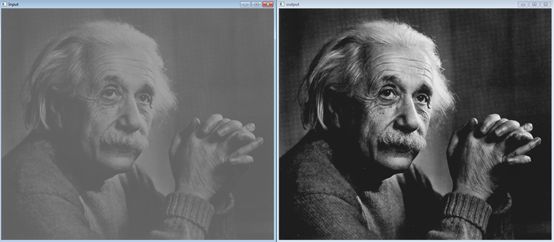
input_img = cv2.imread('F:\program_study\Python\data\Einstein.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', input_img)
img_x1 = 100
img_x2 = 160
img_y1 = 30
img_y2 = 230
SLT_plot(img_x1, img_x2, img_y1, img_y2)
output_img = SLT(input_img, img_x1, img_x2, img_y1, img_y2)
cv2.imshow('output', output_img)
cv2.waitKey(0)
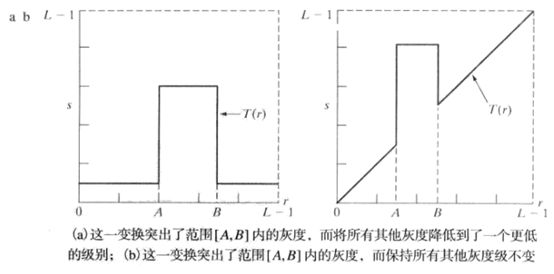
cv2.destroyAllWindows()- 灰度级分层(突出图像特定灰度范围的亮度)
"""灰度级分层"""
import numpy as np
import cv2
def GrayLayer(img):
lut = np.zeros(256, dtype=np.uint8)
layer1 = 30
layer2 = 60
value1 = 10
value2 = 250
for i in range(256):
if i >= layer2:
lut[i] = value1
elif i >= layer1:
lut[i] = value2
else:
lut[i] = value1
ans = cv2.LUT(img, lut)
return ans
img_input = cv2.imread('F:\program_study\Python\data\LandsatImage.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', img_input)
img_output = GrayLayer(img_input)
cv2.imshow('output', img_output)
# cv2.imwrite('LandsatImage_grayLayer.tif', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()- 二值化(阈值化)
"""阈值化，其实就是二值化"""
import cv2
img_input = cv2.imread('F:\program_study\Python\data\Lena.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', img_input)
threshold = 110
img_input[img_input > threshold] = 255 # 二值化
img_input[img_input <= threshold] = 0 # 二值化
cv2.imshow('output', img_input)
# cv2.imwrite('Lena_thresholding.tif', f)
cv2.waitKey(0)
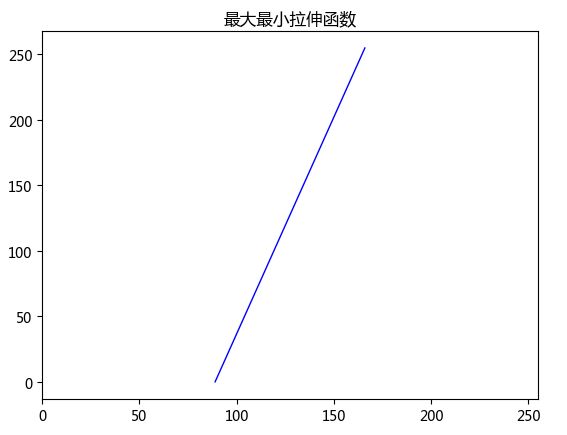
cv2.destroyAllWindows()最大最小值拉伸
"""最大最小值拉伸"""
import numpy as np
import matplotlib.pyplot as plt
import cv2
def max_min_strech(img):
max1 = np.max(img)
min1 = np.min(img)
output_img = (255.0*(img-min1))/(max1-min1) # 注意255.0 而不是255 二者算出的结果区别很大
output_img1 = np.uint8(output_img+0.5)
return output_img1
img_input = cv2.imread('F:\program_study\Python\data\Einstein.tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', img_input)
x = (np.min(img_input), np.max(img_input))
y = (0, 255)
plt.plot(x, y, 'b', linewidth=1)
plt.title('最大最小拉伸函数')
plt.xlim(0, 255)
plt.show()
img_output = max_min_strech(img_input)
cv2.imshow('output', img_output)
cv2.waitKey(0)
cv2.destroyAllWindows()
# 最大最小值拉伸的实质是找线性函数，两点求直线方程，x1是拉伸前的最小值，
# y1是拉伸后的最小值；x2是拉伸前的最大值，y2是拉伸后的最大值--------------------------------------------------------------------------------------------------------------------------------------------------------------------
灰度变换(直方图)
直方图反映了图像像素灰度的分布情况。
直方图均衡化一来可以提高图像的对比度，二来可以把图像变换成像素值是几乎均匀分布的图像。其中心思想是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
我们知道灰度值分布较为平均的图像，通常对比度较高。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同的过程。
1-原理
参考:https://www.zhihu.com/question/37204742/answer/221844779
为简化问题，仅讨论灰度图像的直方图均衡。
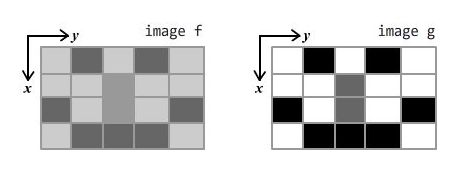
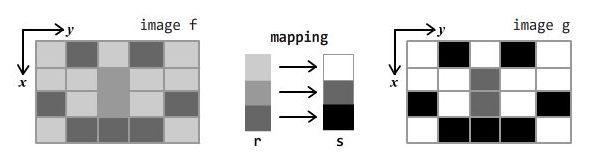
设输入图像为二元函数 f(x, y) ，输出图像为二元函数 g(x, y)，显然二者尺寸相等。我们知道，那些灰度值分布较为平均的图像，通常对比度较高。比如，下图中 g 的灰度较分散（有白的有灰的有黑的），所以对比度较高；f 的灰度很集中，所以显得灰蒙蒙的。直方图均衡的目的，就是对 f 进行处理产生 g，使得 g 的灰度值比 f 更分散。
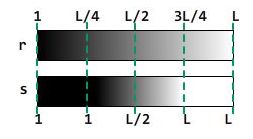
怎么做呢？如果我们有一个恰当的 灰度映射函数 T 就好了，它能把输入灰度值 r 映射为输出灰度值为 s，即 。假设图像的灰度值连续，由黑到白取值为1～L中的实数。灰度映射函数 T 可能长这样：
用图形来表达就是：
对图像施以该灰度映射，图示如下：
看起来不错。不过——有一句老话叫做“具体问题具体分析”，这告诉我们：决不可能使用某个特定的 T 一劳永逸。那么，有没有办法“自动地”根据实际情况生成 T 呢？答案是肯定的。请接着往下看。
设任意灰度值 t 在 f 中出现的概率为函数 ，在 g 中出现的概率为函数 。这两个函数均可以直接由图像统计出来。然后，我们定义两个函数
（意义：f 中灰度值小于 n 的概率）
以及
（意义：g 中灰度值小于 n 的概率）
那么必然有
为什么呢？这是因为我们必须保证：原本比 r 暗的灰度，在变换后依然比 s 暗；原本比 r 亮的灰度，在变换后依然比 s 亮。如果连这一点都不能保证，那么输出的图像就会黑白颠倒一团糟。
比方说，若 ，变换后 。那么，f 中灰度值小于1/3的像素数目 ＝＝ g 中灰度值小于5/2的像素数目。用频率估算概率，也就是 f 中灰度值小于1/3的概率 ＝＝ g 中灰度值小于5/2的概率。还不懂？看图！
弄清楚上面的式子后，自然得到下面的式子（积分后就等于(1) ）：
再接下来，如果我们令变换 ，那么：
其中的第三行，t 是积分变量，真正的自变量是积分上限 r。
由 (2)(3) 得
奇迹出现了：g 中各灰度出现概率相等，为常数1/L。也就是说，各灰度被完全均摊了！
于是我们知道，无论输入图像是什么，只要统计它之中各灰度值出现的概率 ，然后生成映射函数 ，剩下的事就是逐个映射图中灰度即可。
现实中数字图像的灰度值是离散的，对此我们只需略作修改。假设图像最多含有 L 种灰度级，由黑到白依次编号为 。每个灰度级在 f 中出现的概率依次为 ，在 g 中出现的概率依次为 。
函数定义改为： 以及 ，其余同理。
可惜的是，在灰度值离散的情况下，r 和 s 均为整数，我们必须对映射结果取整，这导致 g 中各灰度值出现的概率未必相等。但是可以确定的是： g 的灰度级在一定程度上比 f 更分散了。
2-为什么是累积分布函数
直方图均衡要保证两点：
1、函数映射要保证原图像的大小关系不变。亮区域变换后依然1亮，暗区域变换后依然暗，只是对比度增强了。要保证这一点，映射函数必须单调递增。累积分布函数单调递增。
2、映射范围，原图像[0, 255]，新图像的范围也要[0, 255]，不能超出。累积分布函数值域为[0, 1]可以很好的控制范围。
3-为什么均衡化后灰度是均匀的:
映射函数
r为输入灰度值，s为输出灰度值
概率密度函数
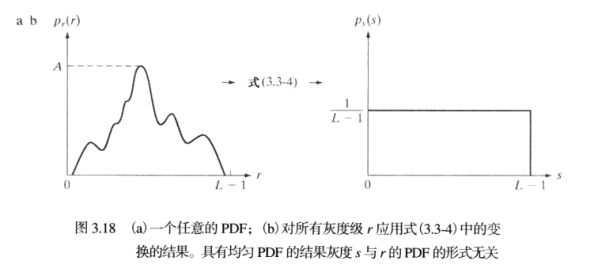
由基本概率论得：如果Pr(r)和T(r)已知，且在感兴趣的值域上T(r)是连续且可微的，则映射后s的概率密度函数由上式计算。其中：Pr(r)为输入灰度值r的概率密度函数，Ps(s)为输出灰度值s的概率密度函数
直方图均衡函数
![\frac{ds}{dr}=\frac{dT(r)}{dr}=(L-1)\frac{d}{dr}[\int_{0}^{r}p_r(r)dr]=(L-1)p_r(r)](http://img.e-com-net.com/image/info8/abde8ec64e8d470ebd1101112cfc0285.gif){kind=small}
推导1
推导2
奇迹出现了，Ps(s)是一个常数，也就是说映射后的新图像概率密度是均匀的，即对比度高。当然这是从结果来推条件了，这样也是为了更容易理解。
实际没这么夸张，一般无法均匀成一条直线
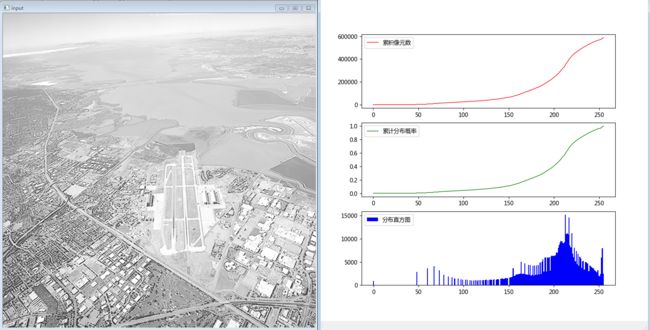
假设有如下图像：
得图像的统计信息如下图所示，并根据统计信息完成灰度值映射：
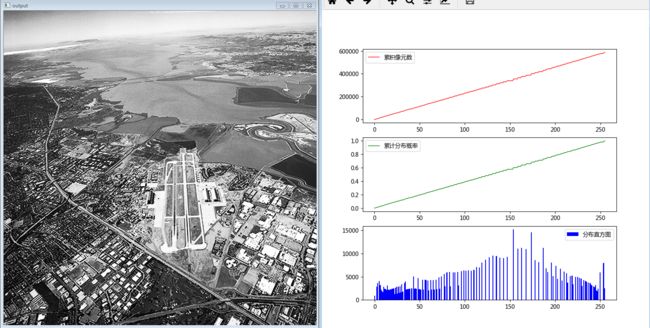
映射后的图像如下所示：
直方图均衡化的映射方程为s = L*T(r) 其中s为映射后的灰度值，L为灰度级8比特255，T(r)为灰度值r的累积分布概率，由分布概率计算得到，分布概率由灰度值r的像元数 / 总像元数得到
实战
"""直方图均衡化"""
import matplotlib.pyplot as plt
import numpy as np
import cv2
# 定义函数，实现图像直方图，累积像元数图和累积分布概率图绘制
def histPlot(hist, cumhist):
plt.figure('辅助图', figsize=(8, 8))
DN = np.arange(256)#横坐标,因为灰度级是0-255所以DN是长为256的元组
plt.subplot(311)
plt.plot(DN, cumhist, 'r', linewidth=1, label='累积像元数')
plt.legend(loc='best')
plt.subplot(312)
plt.plot(DN, cumhist/(769*765), 'g', lw=1, label='累计分布概率') # 769*765为图像行列数，此处投机取巧，无普适性
plt.legend(loc='best')
plt.subplot(313)
plt.bar(DN, hist, color='b', width=1, label='分布直方图')
plt.legend(loc='best')
plt.show()
return
# 定义函数，实现图像的直方图均衡化
def histEqualization(src):
row, col = src.shape
hist, cumhist = histStatistics(src)
# 生成查找表进行直方图均衡化
lut = np.zeros(256, dtype=np.float32)
for i in range(256):
lut[i] = 255.0/(row*col) * cumhist[i] # 均衡化的公式cunhist[i]/(row*col)为累积概率
#这里255就是L-1,后面的项是累积概率(离散的)
#s=T(r)=(L-1)*\sum_hist(i,i
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
空间滤波
空间滤波是在空域进行的滤波操作，有线性空间滤波和非线性空间滤波。线性空间滤波是对目标像素点的领域进行整体考虑，对窗口内的每一个元素乘以系数后求和，并作为目标像素点的响应。非线性空间滤波的思路与线性不同，其操作是非线性的，比如中值滤波、排序滤波等。
空间滤波有很多应用场景，平滑和锐化是两个典型的应用场景。平滑可以使用平滑模板对图像进行线性空间滤波，也可以使用中值滤波对图像进行非线性空间滤波。锐化可以使用锐化模板对图像进行线性空间滤波。
平滑模板示例：
[ 0.1 0.1 0.1
0.1 0.2 0.1
0.1 0.1 0.1 ]
锐化模板示例：
[ 0 1 0
1 -4 1
0 1 0 ]
下面以锐化空间滤波器为例详细介绍:
锐化处理的主要目的是突出灰度的过渡部分。增强边缘和其他突变（噪声），削弱灰度变化缓慢的区域。
注意：垂直方向是x，水平方向是y
1-基础
图像模糊可用均值平滑实现。因均值处理与积分类似，在逻辑上，我们可以得出锐化处理可由空间微分来实现。微分算子的响应强度与图像的突变程度成正比，这样，图像微分增强边缘和其他突变，而削弱灰度变化缓慢的区域。图像积分则削弱边缘,实现平滑.
微分算子必须保证以下几点：
(1)在恒定灰度区域的微分值为0；
(2)在灰度台阶或斜坡处微分值非0；
(3)沿着斜坡的微分值非0
一维函数f(x)的一阶微分定义：
二阶微分定义：
对于二维图像函数f(x,y)是一样的，只不过我们将沿着两个空间轴处理偏微分。
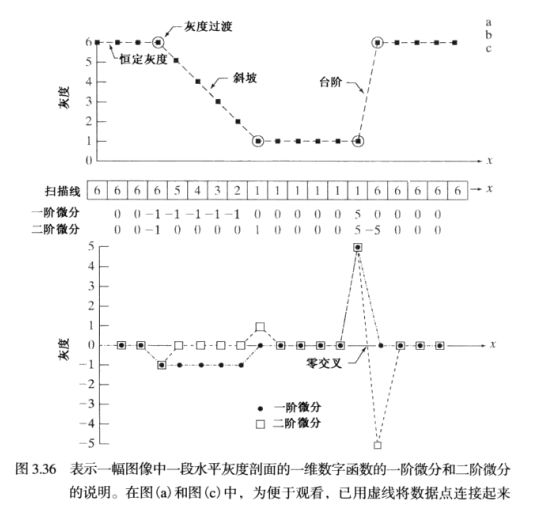
数字图像的边缘在灰度上常常类似于斜坡过渡，这样就导致图像的一阶微分产生较粗的边缘。因为沿着斜坡的微分非0。另一方面，二阶微分产生由0分开的一个像素宽的双边缘。由此我们得出结论，二阶微分在增前细节方面比一阶微分好得多。
2-一阶微分-梯度
函数f(x, y)在(x,y)出的梯度定义为一个二维列向量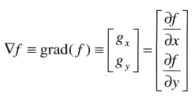
它指出了函数在(x,y)处的最大变化率方向
向量的幅度值（长度）表示为M(x, y)，即
它是最大变化率在(x,y)处的值，M(x,y)是与原图像大小相同的图像，通常称为梯度图像
在某些时候，用绝对值近似计算幅度值：
计算一阶微分
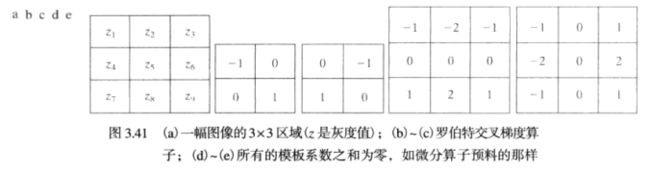
1、Roberts交叉梯度算子[1965]
gx = (z9 - z5) 和 gy = (z8 - z6)
2、Sobel算子
gx = (z7 + 2z8 + z9) - (z1 + 2z2 + z3)
gy = (z3 + 2z6 + z9) - (z1 + 2z4 + z7)
用模板计算出一阶微分后，再根据3.6-11或3.6-12计算梯度图像M(x, y)
3-二阶微分-拉普拉斯算子
我们要的是一个各向同性滤波器，这种滤波器的响应与滤波器作用的图像的突变方向无关。也就是说，各向同性滤波器是旋转不变的，即将原图像旋转后进行滤波处理的结果和先对图像滤波然后再旋转的结果相同。
最简单的各向同性微分算子，即拉普拉斯算子
一个二维图像函数f(x,y)的拉普拉斯算子定义为：
任意阶微分都是线性操作，所以拉普拉斯变换也是一个线性算子。于是：
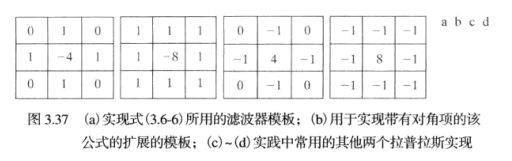
对应的滤波模板为下图a，这是一个旋转90°的各向同性模板，另外还有对角线方向45°的各向同性模板，还有其他两个常见的拉普拉斯模板。a、b与c、d的区别是符号的差别，效果是等效的
拉普拉斯是一种微分算子，因此它强调的是图像中灰度的突变。将原图像和拉普拉斯图像叠加，可以复原背景特性并保持拉普拉斯锐化处理的效果。如果模板的中心系数为负，那么必须将原图像减去拉普拉斯变换后的图像，从而得到锐化效果。所以，拉普拉斯对图像增强的基本方法可表示为下式：
其中，f(x,y)和g(x,y)分别是输入图像和锐化后的图像，如果使用a、b滤波模板则c=-1，如果使用另外两个，则c=1
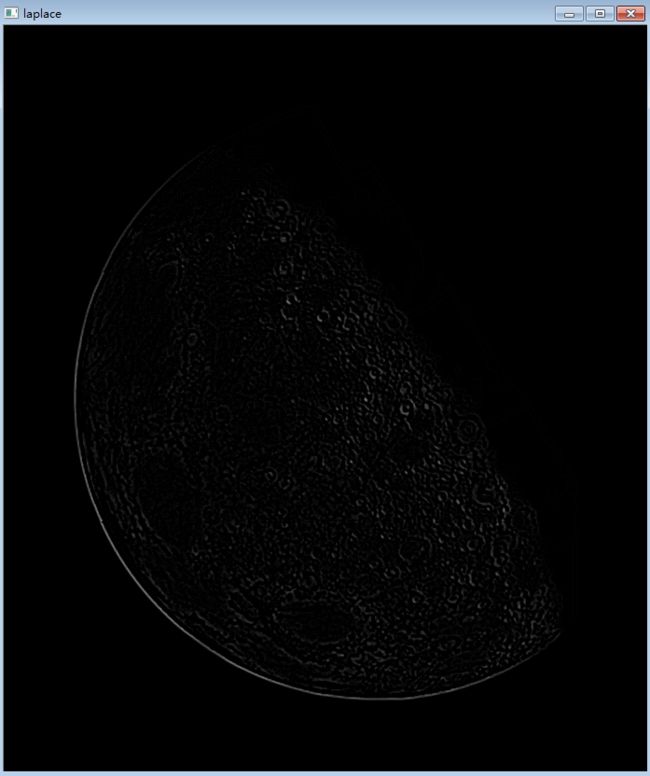
"空间滤波-锐化-拉普拉斯算子"
import numpy as np
import cv2
# 定义函数，实现拉普拉斯算子
def Laplace(src):
template = np.ones((3, 3), dtype=np.float32) # 模板
template[1, 1] = -8.0
addBorderImg = cv2.copyMakeBorder(src, 1, 1, 1, 1, cv2.BORDER_REFLECT_101) #扩充边界
row, col = src.shape
dst = np.zeros((row, col), dtype=np.int16)
for i in range(row):
for j in range(col):
temp = addBorderImg[i:i+3, j:j+3]
dst[i, j] = np.sum(template*temp)
return dst
inputImg = cv2.imread(r'F:\program_study\Python\data\Fig0217(a).tif', cv2.IMREAD_GRAYSCALE)
cv2.imshow('input', inputImg)
laplaceImg = Laplace(inputImg) # 拉普拉斯滤波后的图像
laplaceImg1 = laplaceImg
laplaceImg1[laplaceImg1 < 0] = 0
laplaceImg1 = np.uint8(laplaceImg1)
cv2.imshow('laplace', laplaceImg1)
outputImg = np.zeros(inputImg.shape, dtype=np.float32) # 锐化图像
outputImg = inputImg - laplaceImg
outputImg[outputImg < 0] = 0
outputImg[outputImg > 255] = 255
outputImg = np.uint8(outputImg)
cv2.namedWindow('output', cv2.WINDOW_NORMAL)
cv2.imshow('output', outputImg)
cv2.waitKey(0)
cv2.destroyAllWindows()
'''拉普拉斯算子'''
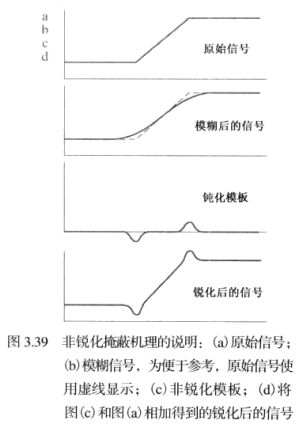
4-非锐化掩蔽和高提升滤波
处理过程：
1、平滑原图像
2、原图像减去1得到的平滑图像（得到的差值图像称为模板）
3、将模板加到原图像上
过程2，
为平滑图像
过程3
k为权重系数，k=1是非锐化掩蔽；k>1是高提升滤波；k<1则不强调非锐化模板的贡献
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
参考链接:
https://blog.csdn.net/qq_39227338/article/details/80108544
https://blog.csdn.net/qq_36771850/article/details/73354389
https://www.cnblogs.com/hizhaolei/p/8051487.html
http://www.cnblogs.com/laumians-notes/p/8629396.html
https://www.cnblogs.com/laumians-notes/p/8275439.html
https://www.cnblogs.com/laumians-notes/p/8708058.html