论文阅读-Deep Residual Learning for Image Recognition
作者: Kaiming He et al.
来源: CVPR 2015
评价: ResNet,Very very deep networks, CVPR best paper
论文链接: https://arxiv.org/pdf/1512.03385.pdf
1 Problem
- the problem and solution:
- problem: the degradation problem. when networks get deeper, accuracy gets saturated and then degrades rapidly, but not caused by overfitting.
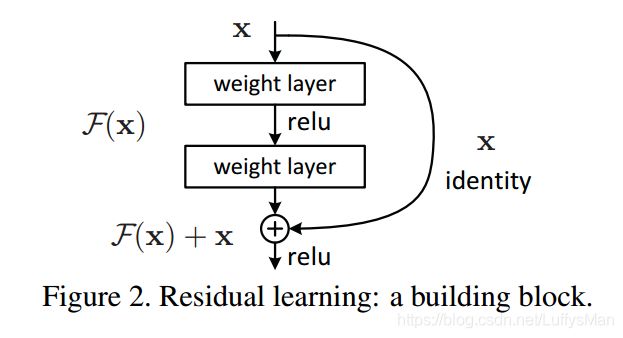
- **original idea residual **: a deeper model should produce no higher training error than its shallower counterpart, with the deeper model is constructed like this: add identity mapping layers on the other layers which are copied from the learned shallower model.
3 The proposed method
The authors present a residual learning framework to ease the training of networks that are substantially deeper than those used previously.
Hypothesis
- They hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. (denoting the desired underlying mapping as H(x), they let the sacked nonlinear layers fit the residual mapping of F(x) := H(x) -x.
- They used the bottleneck architecture to restrain the training time in the deeper version of ResNet(ResNet50 ,110, 152)
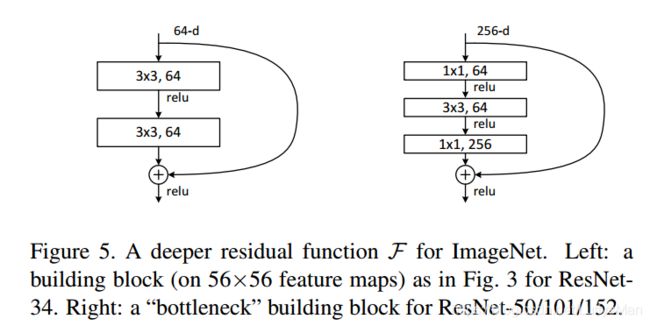
3.1 Advantages:
- The residual networks are easier to optimize;
- Gain accuracy from considerably increased depth;
3.2 Related Work
- Residual Representations.
- H. Jegou et al. Aggregating local image descriptors into compact codes.
TPAMI, 2012. ( VLAD is a representation that encodes by the residual vectors with respect to a dictionary.) - F. Perronnin et al. Fisher kernels on visual vocabularies for image categorization. In CVPR, 2007. (Fsher Vector can be formulated as a probabilistic version of VLAD)
- H. Jegou et al. Aggregating local image descriptors into compact codes.
- Shortcut Connections.
- R. K. Srivastava et al. Highway networks. arXiv:1505.00387, 2015. ( concurrent works of ‘highway networks’)
- R. K. Srivastava, et al. Training very deep networks. 1507.06228, 2015.
3.3 Identity Mapping by Shortcuts
- A building block for residual learning is denoted as:
y = F ( x , W i ) + x y = F(x, {W_i}) + x y=F(x,Wi)+x
x and y are the input and output vectors of the block. - No extra parameters compared with plain networks, so they can fairly compare plain/residual networks that simultaneously have the same number of parameters, depth, width, and computational cost.
3.4 The architecture
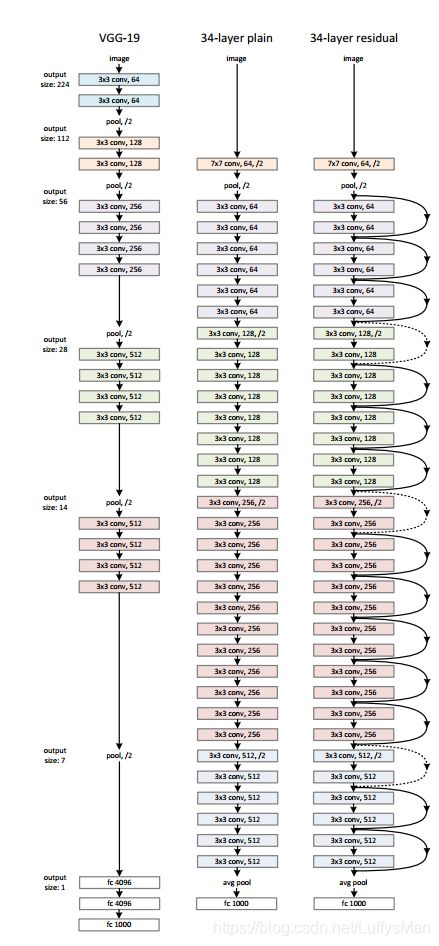
Figure 3. Example network architectures for ImageNet. Left: the VGG-19 model [41] (19.6 billion FLOPs) as a reference. Middle: a plain network with 34 parameter layers (3.6 billion FLOPs). Right: a residual network with 34 parameter layers (3.6 billion
FLOPs). The dotted shortcuts increase dimensions.
- solid line shortcuts in Fig.3: the identity shortcuts can be directly used when the input and output are of the same dimension.
- dotted line shortcuts in Fig.3: the shortcuts go across feature maps of two size and dimension, they are performed with stide of 2, and increase the dimension by either padded with zeros or projection.(projection: y = F ( x , W i ) + W s x y=F(x, {W_i})+W_sx y=F(x,Wi)+Wsx)
3.5 Training Methodology
The authors follow the practice in AlexNet[21] and VGG[41].
- scale augmetation: the image is resized with its shorter side randomly sampled in [256, 480].
- Horizontal flip
- Perpixel mean substract[21]
- Random crop: A 224x224 crop is randomly sampled from an image.
- Standard clolor autmentation[21].
- Batch normalization[16].
- Weight decay, momentum but no dropout.
[16] S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep
network training by reducing internal covariate shift. In ICML, 2015.
[21]A. Krizhevsky, I. Sutskever, and G. Hinton. Imagenet classification
with deep convolutional neural networks. In NIPS, 2012.
[41] K. Simonyan and A. Zisserman. Very deep convolutional networks
for large-scale image recognition. In ICLR, 2015.
3.6 Experiments
-
Observation of the degradation problem. The results in Table 2 show that deeper 34-layer plainnet has higher validation error than the shallower 18-layer plainet.
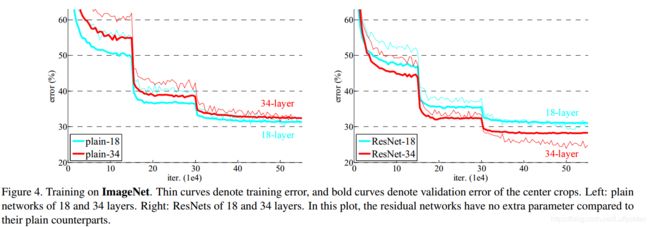
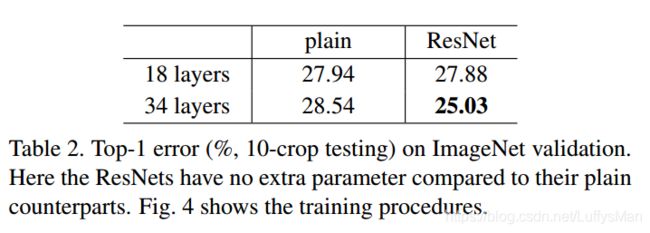
- Hypothesis: the author conjecture that the deep plain nets may have exponentially low convergence rates, which impact the reducing of the traininig error(作者用3倍的迭代次数实验, 依然存在这个退化的问题, 他猜想deep plain nets的指数级低的收敛率, 他们未来再研究. 意思是需要非常多的迭代次数?)
- Residual networks works well, which can be demonstrated in the follow two aspects:
- The situation of degradation is reversed with residual learning.
- Compared to its plain counterpart, the 34 layer ResNet reduces the top-1 error by 3.5%(Table 2).
-
Results in ImageNet.
-
CIFAR-10 and Analysis
The authors focus on extremely deep networks(ResNet1202), so they just inventionally use simple architectures.- Analysis of Layer Responses.
they calcualte standard deviations of the response (outputs of conv op) of plain networks with 20-layer, 56-layer and resnet with layers of 20, 56, 110. And find that ResNets have generally smaller responses than their plain counter parts. - Exploring Over 1000 layers. Unfortunately, there are still open problems on such agressively models. The testing result of this 1202-layer network is worse than that of 110-layer network, although both have similar training error. They author argue that this is because of overfitting. D:)
- Analysis of Layer Responses.
3.5 Data sets
- ILSVRC2015
- PASCAL(detection)
- MS COCO(detection)
3.6 Weakness
- the previous layer need to be stored util convolutional operation is done, and then adding the results of conv operation and the previous layer. which can be memory high cost especially in embedded devices.
4 Future works
Open problems:
- The degradation problem: the plain networks seemed to saturated when their depth attain a reletive large number, but is not because of overfitting. The author conjecture that the deep plain nets may have exponentially low convergence rates, which impact the reducing of the traininig error(作者用3倍的迭代次数实验, 依然存在这个退化的问题, 他猜想deep plain nets的指数级低的收敛率, 他们未来再研究. 意思是需要非常多的迭代次数?)
- ResNet 1202 performs higher validation error than ResNet 110 despite the training error are similar. The author argue that it may be becasue of overfitting but haven’t give firm proofs.
5 What do other researchers say about his work?
-
Kaiming He et al. Identity Mappings in Deep Residual Networks. ARXIV, 2016.
- Deep residual networks [1] have emerged as a family of extremely deep architectures showing compelling accuracy and nice convergence behaviors.
-
Soo Ye Kim et al. 3DSRnet: Video Super-resolution using 3D Convolutional Neural Networks. ARXIV 2018.(ResNet refer to [21] in this work)
- Residual learning was first proposed in [21] and applied to SR in [12]. It also eases training [12] by solving the vanishing and exploding gradient problem which can be critical in training neural networks [22].
-
Christopher B. Choy et al. 3D-R2N2: A Unified Approach for Single and Multi-view 3D Object Reconstruction. ECCV 2016.
- Motivated by a recent study [40], we also created a deep residual variation of the first network and report the performance of this variation in Section 5.2. According to the study, adding residual connections between standard convolution layers effectively improves and speeds up the optimization process for very deep networks.

