Frisch-Waugh定理与部分回归图：图示多元线性回归的系数

 

作者：胡雨霄 (伦敦政治经济学院)
 
Stata 连享会： 知乎 | 简书 | 码云 | CSDN

Stata连享会   计量专题 || 精品课程 || 简书推文 || 公众号合集

 

2019金秋十月-空间计量专题班，杨海生主讲，成都

 

实证研究之初，研究者通常希望可以直观得观察变量 y 与 x 的关系，并以此做出最初关于二者相关关系的基本预判。一个常用的命令是 twoway scatter。该命令允许绘制 y 与 x 的散点图，借此研究者可以对二者关系产生较为直观的认识。然而，这种方式只能非常 粗糙 地描述二者的关系。其原因在于并没有控制其他变量的影响。

计量经济学中，我们认为其粗糙的原因在于遗漏变量偏差 （omitted variable bias）。在尚未控制其他变量影响的情况下，研究者无法断言两个变量相关性的存在，也无法进行量化分析。

而本篇推文介绍的命令 avplot avciplot，xtavplot 则基于部分回归 (partial regression) 的计量原理，在控制了其他变量影响的情况下，允许研究者绘制部分回归图，观测变量 y 与 x 的关系。

 

1. 部分回归：Frisch-Waugh Theorem

部分回归的基本思想是，当引入控制变量后，若想探究解释变量 x1 与被解释变量 y 的相关系数，那么就先 剔除 (partial out) 控制变量对 y 的影响和 剔除 控制变量对 x1 的影响，之后再让剩余部分的 y 对剩余部分的 x1 做回归。

1.1 计量原理

具体而言，假设线性回归方程为

$$\mathrm{y}=\mathrm{X}\beta +\epsilon$$

$\beta$ 为 $K\times 1$ 的系数向量，$ϵ$ 为 $n \times 1 $ 的残差向量。

OLS 估计量 $b$ 满足下式

$$X^{\prime }Xb=X^{\prime }y$$

$X$ 可以被分割为 $ X = [x_1, X2]$，其中 $X_2=[x_2,...,x_k]$。将 $X$ 分割后，$X^{\prime }X$ 可以进一步表示为

$$\left[\begin{array}{cc}{x}_1^{\prime }{x}_1& x_1^{\prime }{X}_2\\ X_2^{\prime }{x}_1& X_2^{\prime }{X}_2\end{array}\right]\text{\hspace{1em}(1)}$$

$X^{\prime }y$ 则可进一步表示为

$$\left[\begin{array}{c}{X}_1^{\prime }y\\ X_2^{\prime }y\end{array}\right]\text{\hspace{1em}(2)}$$

将 （1）式和（2）式代入$X^{\prime }Xb=X^{\prime }y$ 可以得到

由此可以得到两个式子

$$x_1^{\prime }{x}_1{b}_1+x_1^{\prime }{X}_2{b}_2=x_1^{\prime }y$$

$$X_2^{\prime }{x}_1{b}_1+X_2^{\prime }{X}_2{b}_2=X_2^{\prime }y$$

进一步推得

$$X_2^{\prime }{X}_2{b}_2=X_2^{\prime }y-X_2^{\prime }{x}_1{b}_1=X_2^{\prime }(y-x_1{b}_1)$$

也就是说，

$$b_2=(X_2^{\prime }{X}_2{)}^{-1}{X}_2^{\prime }(y-x_1{b}_1)$$

联想 OLS 估计量表达式 $b=(X^{\prime }{X}^{-1})X^{\prime }y$，其实 $b_2$ 可以理解为 $y-x_1{b}_1$ 对 $X_2$ 做回归 $X_2$ 的系数。

经过数学推导后，可以得到

$$b_1=(X_1^{\prime }{M}_2{X}_1{)}^{-1}{X}_1^{\prime }{M}_{2}y$$

其中， $M_2=(I-X_2(X_2^{\prime }{X}_2{)}^{-1}{X}_2^{\prime })$

因为 $M_2$ 是对称 (symmetric) 且幂等 (idempotent) 的，因此 $b_1$ 可以重新写作

$$b_1=(x_1^{\prime }{M}_2^{\prime }{M}_2{x}_1{)}^{-1}{x}_1^{\prime }{M}_2^{\prime }{M}_{2}y=(e_{x1}^{\prime }{e}_{x1}{)}^{-1}{e}_{x1}^{\prime }{e}_y$$

其中，$e_{x1}=M_2{x}_1$，$e_y=M_{2}y$。事实上，$e_y=M_{2}y$ 是 $y$ 对 $X_2$ 做回归后的残差的向量，而 $e_{x1}$ 是 $x_1$ 对 $X_2$ 做回归后的残差的向量。

$e_y$ 和 $e_{x1}$ 也可以被理解为是剔除了 $X_2$ 影响之后的 $y$ 和 $x_1$。因此，$e_y$ 与 $e_{x_1}$ 的散点图即可反映当控制了 $X_2$ 之后， $x_1$ 与 $y$ 的关系。

 

连享会计量方法专题……

1.2 Stata 实现

接下来，我们用 Stata 进一步解释上述原理。

首先，引入数据，并进行基本回归。

sysuse "auto.dta", clear //导入数据
rename (price length weight) (Y X1 X2)
reg Y X1 X2

其基本结果如下。

      Source |       SS           df       MS      Number of obs   =        74
-------------+----------------------------------   F(2, 71)        =     18.91
       Model |   220725280         2   110362640   Prob > F        =    0.0000
    Residual |   414340116        71  5835776.28   R-squared       =    0.3476
-------------+----------------------------------   Adj R-squared   =    0.3292
       Total |   635065396        73  8699525.97   Root MSE        =    2415.7

------------------------------------------------------------------------------
           Y |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
          X1 |  -97.96031    39.1746    -2.50   0.015    -176.0722   -19.84838
          X2 |   4.699065   1.122339     4.19   0.000     2.461184    6.936946
       _cons |   10386.54   4308.159     2.41   0.019     1796.316    18976.76
------------------------------------------------------------------------------

我们可以看到，X1 的系数为 -97.96031，标准误为 39.175。

接下来，我们利用 Frisch-Waugh Theorem 部分回归的原理展示 X1 系数是如何得到的。

第一步，剔除控制变量 X2 对 y 的影响，并保存剩余部分的 y。

reg Y X2
predict ey2, res 

第二步，剔除控制变量 X2 对 X1 的影响，并保存剩余部分的 X1。

reg X1 X2
predict e12, res

第三步，将剩余部分的 y 对剩余部分的 X1 做回归。

reg ey2 e12 

结果如下。我们可以看到 e12 的系数为 -97.96031，与执行 reg Y X1 X2 后 X1 的系数一致。

. reg ey2 e12 

      Source |       SS           df       MS      Number of obs   =        74
-------------+----------------------------------   F(1, 72)        =      6.34
       Model |  36491343.3         1  36491343.3   Prob > F        =    0.0140
    Residual |   414340116        72  5754723.83   R-squared       =    0.0809
-------------+----------------------------------   Adj R-squared   =    0.0682
       Total |   450831459        73  6175773.41   Root MSE        =    2398.9

------------------------------------------------------------------------------
         ey2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
         e12 |  -97.96031    38.9016    -2.52   0.014    -175.5092   -20.41139
       _cons |   1.88e-12   278.8665     0.00   1.000    -555.9103    555.9103
------------------------------------------------------------------------------

 

连享会计量方法专题……

 

2. 图示部分回归图： avplot 与 avplots 命令

avplot 可以实现在控制 $X_2$ 后，观测 $y$ 与 $X_1$ 的关系。该命令的语句十分简洁：

 avplot indepvar [, avplot_options]

其中，

indepvar 是部分回归的解释变量

2.1 avplot 与 twoway scatter 异同分析

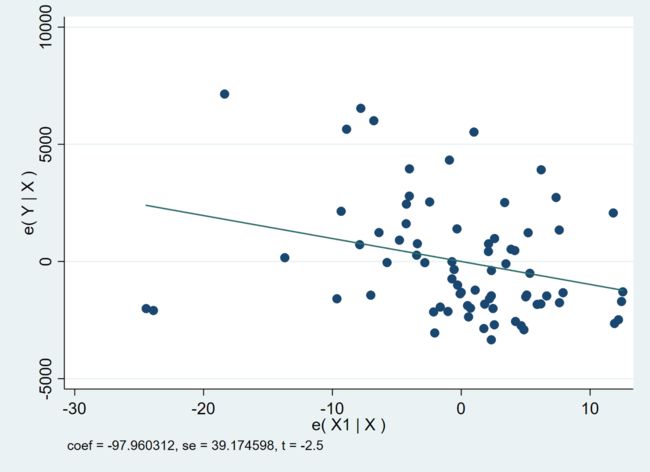
我们在第一部分介绍并用 Stata 展示了部分回归的基本原理。如果想利用 twoway scatter 命令绘制散点图展示 reg Y X1 X2 的结果，那么可以采用命令

twoway (scatter ey2 e12)(lfit ey2 e12)

结果如下

但是，运用 twoway scatter 直观展示回归结果并非效率之举，因为之前要先做回归，并保存结果。avplot 命令则可以一次实现上述操作。命令如下

reg Y X1 X2
avplot X1

我们会发现两幅图别无二致，但 avplot 命令生成的散点图包含了更多与回归结果有关的信息，例如系数、标准误以及 t-统计量。

2.2 一个更为具体的例子

下面，以一个例子来解释在实证中如何运用 avplot 命令。

• 数据的导入

use https://stats.idre.ucla.edu/stat/stata/webbooks/reg/crime

各变量的具体含义如下：

. d

variable name   type    format     label      variable label
------------------------------------------------------------------------------------------------------------
sid             float   %9.0g                 
state           str3    %9s                   
crime           int     %8.0g                 violent crime rate
murder          float   %9.0g                 murder rate
pctmetro        float   %9.0g                 pct metropolitan
pctwhite        float   %9.0g                 pct white
pcths           float   %9.0g                 pct hs graduates
poverty         float   %9.0g                 pct poverty
single          float   %9.0g                 pct single parent
------------------------------------------------------------------------------------------------------------

我们可以看到，这个数据主要记录了不同州的犯罪率的相关资料。

数据结构如下

. list in 1/10

     +-------------------------------------------------------------------------------+
     | sid   state   crime   murder   pctmetro   pctwhite   pcths   poverty   single |
     |-------------------------------------------------------------------------------|
  1. |   1      ak     761        9       41.8       75.2    86.6       9.1     14.3 |
  2. |   2      al     780     11.6       67.4       73.5    66.9      17.4     11.5 |
  3. |   3      ar  r593     10.2       44.7       82.9    66.3        20     10.7 |
  4. |   4      az     715      8.6       84.7       88.6    78.7      15.4     12.1 |
  5. |   5      ca    1078     13.1       96.7       79.3    76.2      18.2     12.5 |
     |-------------------------------------------------------------------------------|
  6. |   6      co     567      5.8       81.8       92.5    84.4       9.9     12.1 |
  7. |   7      ct     456      6.3       95.7         89    79.2       8.5     10.1 |
  8. |   8      de     686        5       82.7       79.4    77.5      10.2     11.4 |
  9. |   9      fl    1206      8.9         93       83.5    74.4      17.8     10.6 |
 10. |  10      ga     723     11.4       67.7       70.8    70.9      13.5       13 |
     +-------------------------------------------------------------------------------+

利用这个数据，我们希望探究州犯罪率 (crime) 的影响因素。crime 是 100,000 人中罪犯的个数。直觉来看，我们认为大都市比例 (pctmetro)，贫穷（poverty），以及单亲父母比例（single）都会影响所在州的犯罪率（crime）。

• 绘制散点图

然后，我们绘制散点图直观观测解释变量与被解释变量的关系。

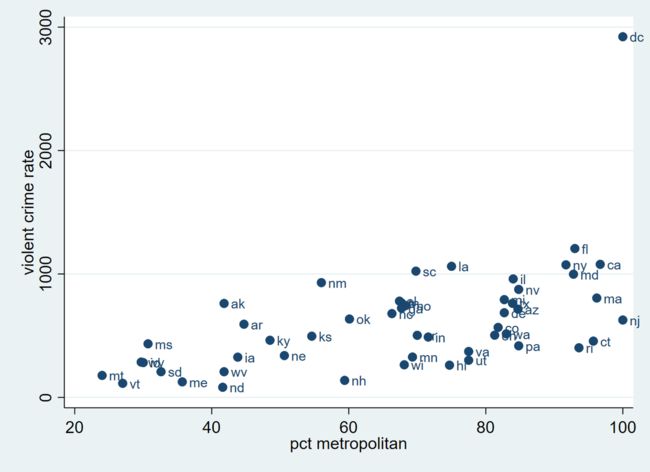
scatter crime pctmetro, mlabel(state)
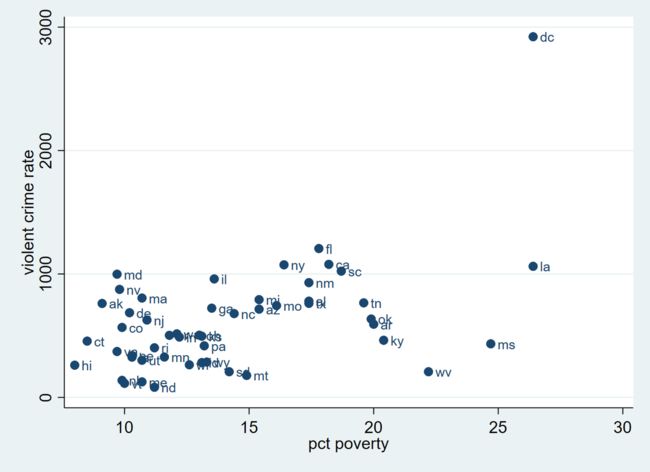
scatter crime pctwhite, mlabel(state)
scatter crime single, mlabel(state)

从这张图我们可以直观看出，一个州的大都市比例越高，那么犯罪率就越高。由此，我们预估，若将犯罪率 crime 对大都市比例 pctmetro 做回归，那么 pctmetro 的系数应该为正。

从这张图我们可以直观看出，一个州的贫穷人口比例越高，那么犯罪率就越高。由此，我们预估，若将犯罪率 crime 对贫穷人口比例 poverty 做回归，那么 poverty 的系数应该为正。

从这张图我们可以直观看出，一个州的单身父母比例越高，那么犯罪率就越高。由此，我们预估，若将犯罪率 crime 对单身父母比例 single 做回归，那么 single 的系数应该为正。

上述图表的绘制并未控制其他变量的影响，因此我们所得出的预估也只是粗糙的。比如，单身父母的产生可能源于较低的收入水平或者和生活地区条件有关。因此，如果控制了 poverty 以及 pctmetro 之后，crime与 single 的关系可能会发生变化。一个合理的猜想是，可能控制其他变量后，二者在图表中的相关性不会如此明显。

• 回归分析

接下来，我们利用 reg 进行基本的回归分析。

. regress crime pctmetro poverty single

      Source |       SS           df       MS      Number of obs   =        51
-------------+----------------------------------   F(3, 47)        =     82.16
       Model |  8170480.21         3   2723493.4   Prob > F        =    0.0000
    Residual |  1557994.53        47  33148.8199   R-squared       =    0.8399
-------------+----------------------------------   Adj R-squared   =    0.8296
       Total |  9728474.75        50  194569.495   Root MSE        =    182.07

------------------------------------------------------------------------------
       crime |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
    pctmetro |   7.828935   1.254699     6.24   0.000     5.304806    10.35306
     poverty |   17.68024    6.94093     2.55   0.014     3.716893     31.6436
      single |   132.4081   15.50322     8.54   0.000     101.2196    163.5965
       _cons |  -1666.436    147.852   -11.27   0.000    -1963.876   -1368.996
------------------------------------------------------------------------------

上图所展示的回归结果基本符合我们通过观察散点图所做出的预判。pctmetro 的系数为 7.829，并且在 1% 的显著性水平上显著。其经济学含义为，当大都市比例增加 1% 时，犯罪率会增加 0.00783%。poverty 的系数为 17.680，并且在 5% 的显著性水平上显著。

其经济学含义为，当贫穷人口所占比例增加 1% 时，犯罪率会增加 0.0177%。single 的系数为 132.408，并且在 1% 的显著性水平上显著。其经济学含义为，当单身父母的比例增加 1% 时，犯罪率会增加 0.132%。

• 部分回归图

得到回归结果之后，我们绘制部分回归图，以期观测在控制其他变量后，犯罪率 crime 与各解释变量之间的关系。

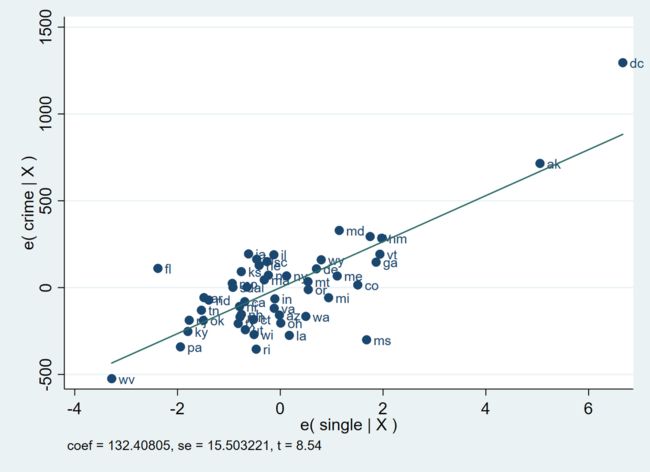
avplot single, mlabel(state)

以 crime 与 single 的部分回归图为例。我们可以看到，纵坐标为 crime 在控制其他变量 （poverty 与 pctmetro）之后的条件均值，而横坐标为控制其他变量（poverty 与 pctmetro）之后 single 的条件均值。

此外，我们可以发现，该表完美得展现了 crime 对 single 部分回归的结果，不论是系数，标准误，或者 t-统计量，都与回归的结果完全一致。

我们再与散点图进行比较，可以发现，虽然基本趋势仍保持不变，但是散点图明显更为陡峭。这也说明之前的猜测是合理的。当控制其他变量后，直观来看，crime 与 single 的相关性就不是那么明显了。

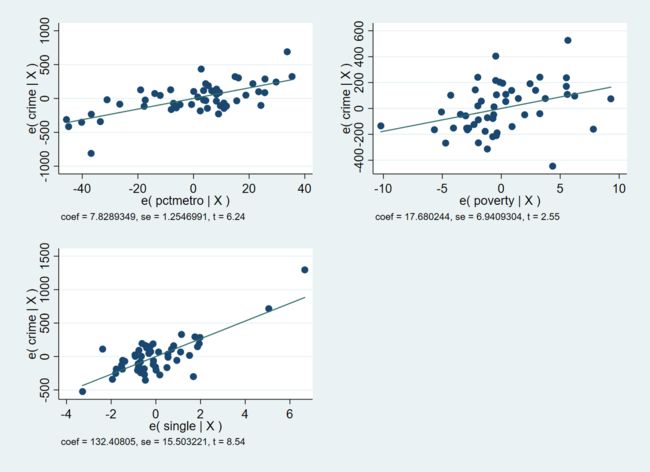
此处，介绍另一个好用的命令 avplots。该命令可以将不同的部分回归图合并为一张图表输出。如下，直接键入

avplots

我们可以得到下图。

这一张图输出了三张部分回归图。与 crime 与 single 的部分回归图相同，crime 与 pctmetro, poverty 的部分回归图分别完美展现了 crime 对 pctmetro 以及 poverty 部分回归的结果。

3. 带置信区间的部分回归图 avciplot 与 avciplots

若希望绘制带置信区间的部分回归图，那么可以利用 avciplot 与 avciplots 命令。该命令的基本语法与 avplot 以及 avciplots 基本一致，只是允许绘制置信区间。

• 命令的安装

ssc install avciplot

• 带置信区间的部分回归图

运行如下命令，我们即可得到一张包含三个部分回归图的汇总图表。而每个部分回归图还绘制了置信区间。

avplots

如上图所示，红色虚线之间的部分则为置信区间。

4. 面板数据的部分回归图 xtavplot

处理面板数据时，我们需要考虑固定效应。因此，用 Stata 绘制面板数据的部分回归图时，我们选用的命令不同于上，而使用针对面板数据的命令，xtavplot。但其基本语句与 avplot 十分类似。

 xtavplot indepvar [, options]

其中，

indepvar 是部分回归的解释变量

generate (exvar eyvar) 允许对残差变量，也就是剔除控制变量影响后的变量，进行保存

ciunder 允许加入置信区间

ciplot() 允许特别设定置信区间的绘制方法

• 数据导入

webuse nlswork

各变量的具体含义如下

. d
variable name   type    format     label      variable label
------------------------------------------------------------------------------------------------------------
idcode          int     %8.0g                 NLS ID
year            byte    %8.0g                 interview year
birth_yr        byte    %8.0g                 birth year
age             byte    %8.0g                 age in current year
race            byte    %8.0g      racelbl    race
msp             byte    %8.0g                 1 if married, spouse present
nev_mar         byte    %8.0g                 1 if never married
grade           byte    %8.0g                 current grade completed
collgrad        byte    %8.0g                 1 if college graduate
not_smsa        byte    %8.0g                 1 if not SMSA
c_city          byte    %8.0g                 1 if central city
south           byte    %8.0g                 1 if south
ind_code        byte    %8.0g                 industry of employment
occ_code        byte    %8.0g                 occupation
union           byte    %8.0g                 1 if union
wks_ue          byte    %8.0g                 weeks unemployed last year
ttl_exp         float   %9.0g                 total work experience
tenure          float   %9.0g                 job tenure, in years
hours           int     %8.0g                 usual hours worked
wks_work        int     %8.0g                 weeks worked last year
ln_wage         float   %9.0g                 ln(wage/GNP deflator)
------------------------------------------------------------------------------------------------------------
Sorted by: idcode  year
     Note: Dataset has changed since last saved.

我们可以看到该数据包含了受访者的基本个人信息，教育信息以及工作信息。数据结构如下。

• 固定效应回归

我们希望探究工资与工作年限的关系，并利用固定效应模型进行回归分析。

. xtreg ln_w ttl_exp age c.age#c.age not_smsa south, fe

Fixed-effects (within) regression               Number of obs     =      1,000
Group variable: idcode                          Number of groups  =        163

R-sq:                                           Obs per group:
     within  = 0.1679                                         min =          1
     between = 0.2150                                         avg =        6.1
     overall = 0.1843                                         max =         15

                                                F(5,832)          =      33.57
corr(u_i, Xb)  = 0.1188                         Prob > F          =     0.0000

------------------------------------------------------------------------------
     ln_wage |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
     ttl_exp |    .042675   .0055722     7.66   0.000     .0317377    .0536124
         age |   .0126192   .0131824     0.96   0.339    -.0132556    .0384939
             |
 c.age#c.age |  -.0003629   .0002166    -1.68   0.094    -.0007881    .0000623
             |
    not_smsa |  -.0487662   .0714594    -0.68   0.495    -.1890281    .0914957
       south |  -.0905245   .0997515    -0.91   0.364    -.2863187    .1052696
       _cons |   1.535607   .1934652     7.94   0.000      1.15587    1.915345
-------------+----------------------------------------------------------------
     sigma_u |  .34777879
     sigma_e |  .27590435
         rho |  .61373148   (fraction of variance due to u_i)
------------------------------------------------------------------------------
F test that all u_i=0: F(162, 832) = 7.55                    Prob > F = 0.0000

在这个固定效应回归中，我们控制了年龄 （age），年龄的交互（c.age#c.age)，非来自大都市的虚拟变量(not_smsa）以及来自南方的虚拟变量（south）。

回归结果如上所示。我们可以看到，工作年限（ttl_exp）的系数为 0.043，且在 1% 的显著性水平上显著。其经济学含义为，当工作年限增加 1 年时，工资增加 4.27%。这说明，工作年限与工资水平显著正向相关。

• 部分回归图

下面，我们用 xtavplot 命令来绘制该面板数据的部分回归图。因为我们最关心的解释变量就工作年限（ttl_exp），因此绘制一张部分回归图即可。

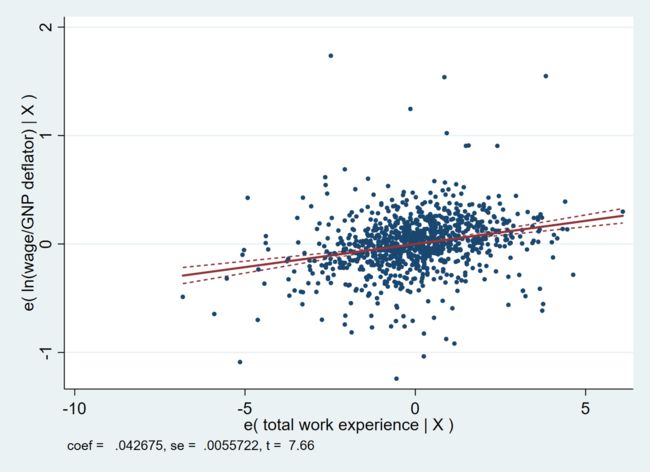
xtavplot ttl_exp, ciunder

如上图所示。其纵轴为控制了其他控制变量后，ln(wage/GNP deflator) 的条件均值。其横轴为控制了其他控制变量后，total work experience 的条件均值。

红色实线为拟合的部分回归线。我们可以看到，其系数、标准误以及 t-统计量都与部分回归中 ttl_exp 的一致。

通过设置 ciunder，部分回归图可以加入置信区间，即为图中的红色虚线部分。

5. 总结

这篇推文介绍了如何在 Stata 中绘制部分回归图。具体而言，我们介绍了三个命令：avplot，avciplot，以及xtavplot。

 

连享会计量方法专题……

 

关于我们

• 【Stata 连享会(公众号：StataChina)】由中山大学连玉君老师团队创办，旨在定期与大家分享 Stata 应用的各种经验和技巧。
• 公众号推文同步发布于 CSDN-Stata连享会 、简书-Stata连享会 和 知乎-连玉君Stata专栏。可以在上述网站中搜索关键词Stata或Stata连享会后关注我们。
• 点击推文底部【阅读原文】可以查看推文中的链接并下载相关资料。
• Stata连享会 精品专题 || 精彩推文

联系我们

• 欢迎赐稿： 欢迎将您的文章或笔记投稿至Stata连享会(公众号: StataChina)，我们会保留您的署名；录用稿件达五篇以上，即可免费获得 Stata 现场培训 (初级或高级选其一) 资格。您也可以从 连享会选题平台 → [002_备选主题] 中选择感兴趣的题目来撰写推文。
• 意见和资料： 欢迎您的宝贵意见，您也可以来信索取推文中提及的程序和数据。
• 招募英才： 欢迎加入我们的团队，一起学习 Stata。合作编辑或撰写稿件五篇以上，即可免费获得 Stata 现场培训 (初级或高级选其一) 资格。
• 联系邮件： [email protected]

往期精彩推文

• Stata连享会推文列表
• Stata连享会 精品专题 || 精彩推文

---