PAISR:Rapid and Accurate Image Super Resolution 详解(内附代码code)
hi,这绝对是一篇想搞事情的博客,本宝对这篇文章也没有弄得很透彻,甚至在某些小块上卡住了,但是还是有些干货想跟小伙伴们分享,顺便一起探讨一些问题。
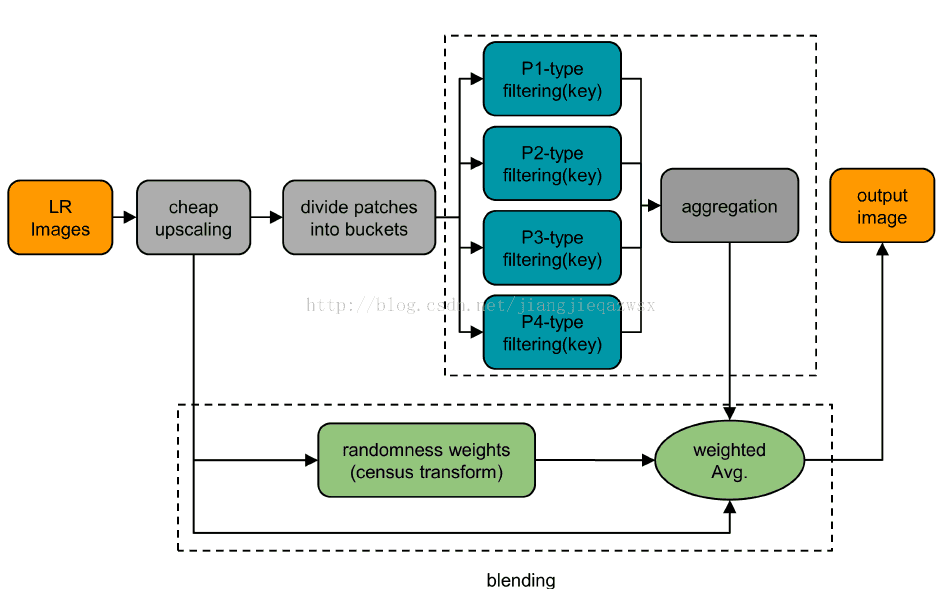
在github:https://github.com/HerrHao/RAISR上有研友写了部分代码,并没有完全实现论文,虽然效果也不怎样理想,但是使用滤波器的方法代替字典速度提高了好多。不多说了,下面是论文的框架
主要分为以几个部分:
1)对图像进行简单的插值;
2)使用哈希机制对图像块进行分类;
3)对每一类图像块训练四个滤波器;
4)对使用滤波器重建后的图像使用CT-Bleng方法消除可能带来的伪影;
5)获得高分辨率图像。
我对论文的哈希分桶比较感兴趣,所以下面将讲述一些它的原理。
使用图像块的局部结构描述子对图像进行描述,然后使用这个 描述子对图像分桶。在这里的描述子,作者通过计算局部图像的梯度相关信息,获得图像块的角度、相关性、强度,对它们进行量化后,形成一个向量。然后这三个向量视为一个坐标,把一个三维的坐标转化成一个数字来表示桶的编号。图像信息量化的代码如下:
% function [theta]=hashTable(patch,Qangle,Qstrenth,Qcoherence)
function [theta,lamda,u]=hashTable(patch,Qangle,Qstrenth,Qcoherence)
[q1,q2]=gradient(patch);
q1=q1(:);
q2=q2(:);
G=[q1,q2];
% G(:,1)=zscore(G(:,1));
% G(:,2)=zscore(G(:,2));
x=G'*G;
[V,D]=eig(x);
theta=atan2(V(1,1),V(2,1));
if(theta<0)
theta=theta+pi;
end
% theta = theta/pi*180;
D=[D(1,1),D(2,2)];
lamda=max(D)/(sum(D)+0.0001);
sroot=sqrt(D);
% lamda = max(sroot);
u=abs((sroot(1)-sroot(2))/(sroot(1)+sroot(2)+0.0001));
theta=floor(theta/(pi/Qangle))+1;
lamda=floor(lamda/(1/Qstrenth))+1;
u=floor(u/(1/Qcoherence))+1;
if(theta == 25)
theta = 24;
end
if(lamda == 4)
theta = 3;
end
if(u == 4)
u = 3;
end
end在这里,我们把角度,相关性,强度分别量化在24,3,3三个数量值内,为什么是这三个呢?其实我们可以看论文中的滤波器的图:
每个图像块表示一个滤波器,其中红、绿、黄分别代表角度,强度,相关性的编号方式,如果如果把量化后的向量(角度,相关性,强度)视为一个坐标,转化成一维的数字,则应该满足下面的关系式:
index = 9*(角度-1)+3*(相关性-1)+强度
当我们使用哈希的方法把图像块划分到K个桶里作为训练滤波器的时候,为了保证训练的效果,意味着每个图像桶里都至少需要1万数量图像块。然而在现实中,相比于提供1万*K数量的图像块,现实中使用我们的训练图库对每个桶提供1万的图块难多了。其原因是,在自然图像中,有些结构反复出现,而有些结构则出现得非常少,这将导致通过哈希函数分类后,有些桶里面的图像块数量非常多,有些桶却是空的或者图像块数量很少。例如,在图像中有很多水平和垂直的结构,而平坦区域(例如天空和平坦的平面)相对少一点。所以觉见的结构会产生常见的哈希值。
所以作者提出对图像的样本进行一个对称变换,增加样本的结构。
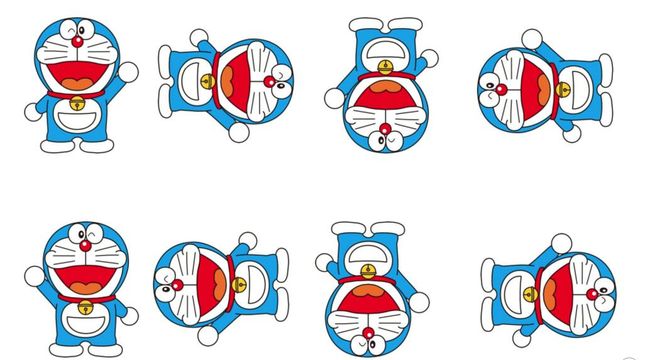
感觉作者的意思是:只要对图像进行4个旋转和进行镜像后使用4个旋转,它的(角度,相关性,强度)向量就会变化 ,即下面8种情况:
但是我使用hashTable.m测试了一下,只有三种图像变换会改变这个向量:旋转90度,y轴镜像对称,y轴镜像对称后再旋转90度,而且只有角度发生了变化 。
作者在论文中,下面是在极坐标下角度的对称图:
从图中我们可以看出作者做的变换其实也是角度的一个变换,但是难点是:我们使用这个方法是为了得到更多的图像块结构,而作者图中的图像块按箭头进行变化,映射到我们的图像块中又是一个什么变换呢?我只找到了三种变换,实现了一个[0,pi]的变换。它说的8倍的变换是什么?
%%%%%%%%%%%%%%%%%%%%%
我以前会觉得量化是这篇文章最简单的,后来发现不是的,量化里面包含了很多设计。
例如,目前我们按前面的代码进行量化,存在两个问题:
1.量化后的lamda只能是2或者3;
2.哈希桶很规律的出现空桶;
经过分析,造成1的原因是
lamda=max(D)/(sum(D)+0.0001);这个表达式子会造成lamda的范围是[0.5, 1],当然不可能量化为1;
造成问题2的原因是:
lamda=floor(lamda/(1/Qstrenth))+1;
u=floor(u/(1/Qcoherence))+1;lamda与u有很大的相关性;
所以如何进行归一化,如何去掉这种相关性,如何保证每个桶都不为空是个很有学问的事情, 所以你们有什么想法吗,?欢迎给我博客留言,或者邮件[email protected].
这是由Charles,HerrHao等贡献的写的基本算法,包括hashtable的实现,CT-Blengding,滤波器的显示,滤波器的训练和图像重建。
https://pan.baidu.com/s/1cvvsvW
参考资料
https://github.com/movehand/raisr
https://github.com/MKFMIKU/RAISR
https://github.com/HerrHao/RAISR
与朋友的交流邮件