leetcode | 123. Best Time to Buy and Sell Stock III

题目

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
             Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.

Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

思路与解法

从题目可知，我们可以先计算第一次买卖股票所获得收益，进行保存，然后再计算买卖第二次买卖股票的收益（与第一次不冲突）加上第一次买卖股票的收益最终取最大值即可。

方法一：

我们可用dp[i][1]表示第i天为止进行一次买卖股票的最大收益；dp[i][2]表示第i天为止进行两次买卖股票的最大收益。

代码实现

func max(a, b, c int) (maxx int) {
    maxx = a
    if maxx < b {
        maxx = b
    }
    if maxx < c {
        maxx =c
    }
    return
}
func maxProfit(prices []int) int {
    days := len(prices)
    dp := make([][]int, 0)
    for i:=0; i<=days; i++ {
        dp = append(dp, make([]int, 3))
    }

    for i:=1; i<=days; i++ {
    	// 第i天第一次买卖股票的收益默认为前一天的收益
        dp[i][1] = dp[i-1][1]
        // 以第j天为分界线，在[1~j-1]天寻找第一天收益 + 区间[j+1~i]第二天收益的最大值
        // dp[i][2]存储第i天为止进行两次股票买卖的最大值。
        for j:=1; j<i; j++ {
            if prices[i-1] - prices[j-1] > dp[i][1] {
                dp[i][1] = prices[i-1] - prices[j-1]
            }

            for k:=j+1; k<i; k++ {
                if dp[j][1] + prices[i-1] - prices[k-1] > dp[i][2] {
                    dp[i][2] = dp[j][1] + prices[i-1] - prices[k-1]
                }
            }
            dp[i][2] = max(dp[i][2], dp[i-1][2], dp[i][1])
        }
    }
    return dp[days][2]
}

运行结果

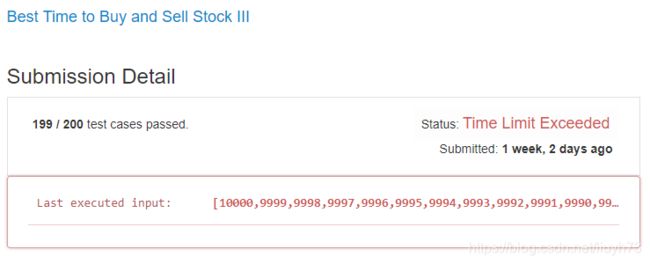
上述代码实现效率很低，$O(N^3)$

方法二：

换一种思路，我们可以首先顺序计算，得到第i天为止进行一次股票买卖的最大收益保存为f[i]；然后倒序计算maxx - prices[i] + f[i-1]的最大值（maxx初始值为prices[days-1]，maxx保存的是股票的最大价值，详情见下方代码），即为两次股票买卖的最大收益。

代码实现

func max(a, b int) int {
    if a < b {
        return b
    }
    return a
}

func maxProfit(prices []int) int {
    days := len(prices)
    if days == 0 {
        return 0
    }
    f := make([]int, days)
    minn := prices[0]
    maxx := prices[days-1]
    sum := 0
    // f[0]收益为0，所以无需计算
    for i:=1; i<days; i++ {
        if prices[i] > prices[i-1] {
            f[i] = max(f[i-1], prices[i] - minn)
        } else {
            f[i] = f[i-1]
        }

        if prices[i] < minn {
            minn = prices[i]
        }
    }
	// 两次股票买卖的最大收益为max(sum, maxx - prices[i] + f[i-1])
    for i:=days-1; i>0; i-- {
        maxx = max(maxx, prices[i])
        if maxx - prices[i] > 0 {
            sum = max(sum, maxx - prices[i] + f[i-1])
        }
    }
	// 注意处理边界问题
    if maxx - prices[0] > 0 {
        sum = max(sum, maxx - prices[0])
    }

    return sum 
}

运行结果