深度学习课程 | 《卷积神经网络》概念笔记——卷积神经网络
卷积神经网络
- 1. padding
- 2. 卷积步长
- 3. 单层卷积网络
- 3. 池化层
- 4. 全连接层
- 5. 经典网络
- 6. 残差网络 Residual Networks(ResNets)
- 7. Inception 网络
- 8. 数据增强 Data Augmentation
- 9. 滑动窗口算法
- 10. 边界框预测 Bounding Box Predictions
- 11. 交并比 IoU
- 12. 非最大抑制 NMS
- 13. Anchor Boxes
- 14. RPN网络
- 15. add和concat的不同
1. padding
padding译为扩充,对原始图片尺寸进行扩充,一般使用“0”。
在卷积过程中,如果原始图片尺寸是n×n,filter尺寸是f×f,则卷积后的图片尺寸是(n-f+1)×(n-f+1),一般f取奇数。
经过上面卷积操作,可能会导致两个问题:
- 卷积后,输出图片尺寸缩小;
- 原始图片边缘信息对输出图片贡献比较少,输出图片会丢失边缘信息。
为了解决这个问题,因此使用padding方法,把原始图片尺寸进行扩充。
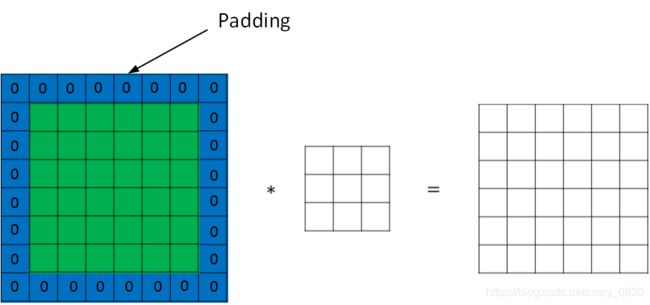
经过padding之后,原始尺寸变为(n+2p) x (n+2p),filter还是f×f,输出图片尺寸则变为(n+2p-f+1) x (n+2p-f+1)。
若要保证卷积前后图片尺寸大小不变,则p应该为: p = f − 1 2 p = \frac{f-1}{2} p=2f−1
valid conv: 表示没有进行padding操作,即p=0。
same conv: 表示输入和输出是一致的尺寸,p用上面的公式计算。
2. 卷积步长
步长stride表示filter在图片尺寸中水平方向和垂直方向每次进行的步进长度。默认是stride = 1。若stride = 2表示filter每次步进长度是2,即每隔一个点移动一次。
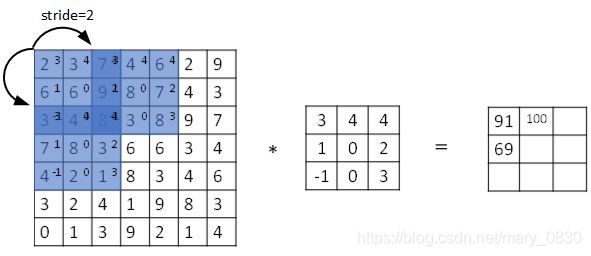
同样的,原始图片尺寸是n x n,filter尺寸为f x f,那么卷积后的图片尺寸是: ⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ \left \lfloor \frac{n+2p-f}{s}+1 \right \rfloor ×\left \lfloor \frac{n+2p-f}{s}+1 \right \rfloor ⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋其中,上面符号表示向下取整,即选取不大于该值的整数。
在目前深度学习领域,使用的卷积操作其实是相关系数操作,因为能够这样等价,是因为滤波器算子一般是水平或者垂直对称的,180°旋转影响并不大,而且最后滤波器算子需要通过CNN网络梯度下降算法计算得到,旋转部分可以看作是包含在CNN模型算法中的。
3. 单层卷积网络
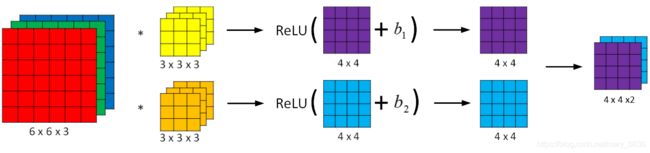
CNN的单层结构多了激活函数ReLU和偏移量b。整个卷积过程和标准的神经网络单层结构很相似。卷积对应着乘积运算,滤波器组的数值对应着权重 W [ l ] W^{[l]} W[l],激活函数 g [ l ] g^{[l]} g[l]选的是ReLU。
Z [ l ] = W [ l ] A [ l − 1 ] + b Z^{[l]}=W^{[l]}A^{[l-1]}+b Z[l]=W[l]A[l−1]+b
A [ l ] = g [ l ] ( Z [ l ] ) A^{[l]}=g^{[l]}(Z^{[l]}) A[l]=g[l](Z[l])
卷积操作的参数是与输入图片大小无关的,由滤波器组的参数来决定的。例如,每个滤波器组有3x3x3=27个参数,还有1个偏移量b,则每个滤波器组有27+1=28个参数,两个滤波器组总共包含28x2=56个参数。
单层卷积网络的参数总结:
- f [ l ] f^{[l]} f[l]:filter size
- g [ l ] g^{[l]} g[l]:padding大小
- s [ l ] s^{[l]} s[l]:stride大小
- n c [ l ] n_{c}^{[l]} nc[l]:filters的数量
- 输入维度: n H [ l − 1 ] × n W [ l − 1 ] × n c [ l − 1 ] n_{H}^{[l-1]}\times n_{W}^{[l-1]}\times n_{c}^{[l-1]} nH[l−1]×nW[l−1]×nc[l−1]
- 每个滤波器组的维度: f [ l ] × f [ l ] × n c [ l − 1 ] f^{[l]}\times f^{[l]}\times n_{c}^{[l-1]} f[l]×f[l]×nc[l−1]
- 权重维度: f [ l ] × f [ l ] × n c [ l − 1 ] × n c [ l ] f^{[l]}\times f^{[l]}\times n_{c}^{[l-1]}\times n_{c}^{[l]} f[l]×f[l]×nc[l−1]×nc[l]
- 偏置维度: 1 × 1 × 1 × n c [ l ] 1\times 1\times 1\times n_{c}^{[l]} 1×1×1×nc[l]
- 输出维度: n H [ l ] × n W [ l ] × n c [ l ] n_{H}^{[l]}\times n_{W}^{[l]}\times n_{c}^{[l]} nH[l]×nW[l]×nc[l]
- 其中, n H [ l ] = ⌊ n H [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n_{H}^{[l]}=\left \lfloor \frac{n_{H}^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}} +1\right \rfloor nH[l]=⌊s[l]nH[l−1]+2p[l]−f[l]+1⌋
n W [ l ] = ⌊ n W [ l − 1 ] + 2 p [ l ] − f [ l ] s [ l ] + 1 ⌋ n_{W}^{[l]}=\left \lfloor \frac{n_{W}^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}} +1\right \rfloor nW[l]=⌊s[l]nW[l−1]+2p[l]−f[l]+1⌋
如果有m个样本,则进行向量化运算,输出维度为: m × n H [ l ] × n W [ l ] × n c [ l ] m\times n_{H}^{[l]}\times n_{W}^{[l]}\times n_{c}^{[l]} m×nH[l]×nW[l]×nc[l]
3. 池化层
定义: 池化层是用于CNN中用来减小尺寸的,提高运算速度的,减小噪声的影响,让特征更具有鲁棒性。
池化层分为:Max pooling和 Average pooling。
Max pooling的优势在于保留区域内的最大值(特征),忽略其他值,降低噪声的影响。Max pooling需要的超参数为滤波器尺寸 f f f和步长 s s s,不需要其他的参数。
Average pooling是滤波器算子滑动区域计算平均值,同样只需要滤波器尺寸 f f f和步长 s s s。
在实际应用中,Max pooling比Average pooling更常用。
4. 全连接层
定义: 全连接层中的每个神经元与前一个层的所有神经元进行全连接,整合前面卷积层与池化层的信息。全连接的核心操作就是矩阵向量乘积。
作用: 在CNN中起到”分类器“的作用
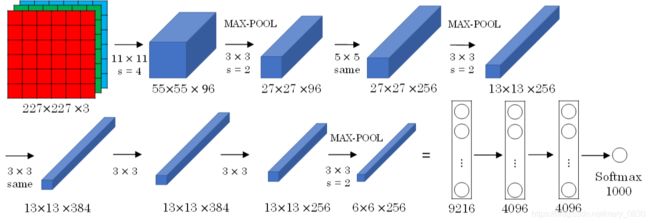
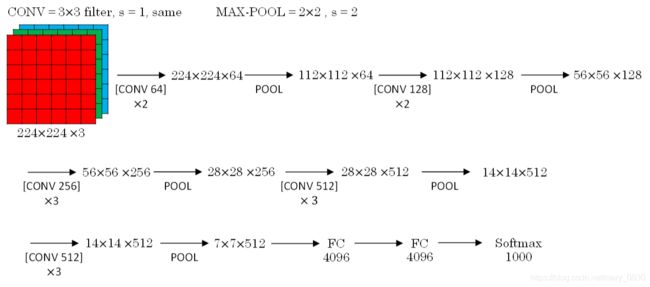
5. 经典网络
6. 残差网络 Residual Networks(ResNets)
定义: 当CNN层数增多,网络越深时,可能会引起梯度消失和梯度爆炸,使得整个网络模型不能进行更好地训练或者不能到达拟合,因此就需要采取一种弱化每层相互关系的方法,为的是能够训练更深的网络。这种方法是人为地让神经网络某些层跳过下一层神经元的连接,隔层或者各几层相连。
如下图表示的是Residual block:
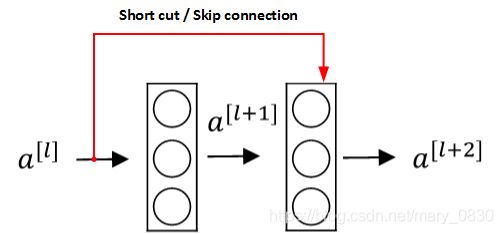
下图表示的是Residual Network:

为什么ResNets能够训练更深的神经网络?

输入x经过Big NN后,输出的是 a [ l ] a^{[l]} a[l], a [ l ] a^{[l]} a[l]经过一个Residual block输出 a [ l + 2 ] a^{[l+2]} a[l+2]。 a [ l + 2 ] a^{[l+2]} a[l+2]表达式为: a [ l + 2 ] = g ( z [ l + 2 ] + a [ l ] ) = g ( W [ l + 2 ] a [ l + 1 ] + b [ l + 2 ] + a [ l ] ) a^{[l+2]}=g(z^{[l+2]}+a^{[l]})=g(W^{[l+2]}a^{[l+1]}+b^{[l+2]}+a^{[l]}) a[l+2]=g(z[l+2]+a[l])=g(W[l+2]a[l+1]+b[l+2]+a[l])
若 W [ l + 2 ] ≈ 0 W^{[l+2]}≈0 W[l+2]≈0, b [ l + 2 ] ≈ 0 b^{[l+2]}≈0 b[l+2]≈0,且当 a [ l ] ≥ 0 a^{[l]}≥0 a[l]≥0,有: a [ l + 2 ] = g ( a [ l ] ) = R e L U ( a [ l ] ) = a [ l ] a^{[l+2]}=g(a^{[l]})=ReLU(a^{[l]})=a^{[l]} a[l+2]=g(a[l])=ReLU(a[l])=a[l]
从公式可以知道,即使发生梯度消失或者梯度爆炸,也能够得到恒等公式: a [ l + 2 ] = a [ l ] a^{[l+2]}=a^{[l]} a[l+2]=a[l]。因此,整个过程就相当于忽略了 a [ l + 1 ] a^{[l+1]} a[l+1],弱化了某些神经层之间的联系,就能够训练更深的神经网络了。
如果Residual blocks中 a [ l ] a^{[l]} a[l]和 a [ l + 2 ] a^{[l+2]} a[l+2]的维度不同,则需要引入 W s W_{s} Ws,与 a [ l ] a^{[l]} a[l]相乘,使得 W s ∗ a [ l ] W_{s}*a^{[l]} Ws∗a[l]的维度与 a [ l + 2 ] a^{[l+2]} a[l+2]一致。
那么参数 W s W_{s} Ws该怎么计算得到呢?
第一,将 W s W_{s} Ws作为学习参数,通过模型训练得到;第二,设置固定的 W s W_{s} Ws值,不需要训练, W s W_{s} Ws与 a [ l ] a^{[l]} a[l]的乘积只需要将 a [ l ] a^{[l]} a[l]截断或者补零。
7. Inception 网络
作用: 代替人工来确定卷积层中的过滤器类型或是否需要创建卷积层或池化层。该网络是使用不同尺寸的滤波器,并将卷积层和池化层结合起来使用,将所有的输出组合拼接起来,再由神经网络本身去学习参数并选择最佳的模块。
不足: Inception 网络会导致计算量过大的问题。如下图所示:
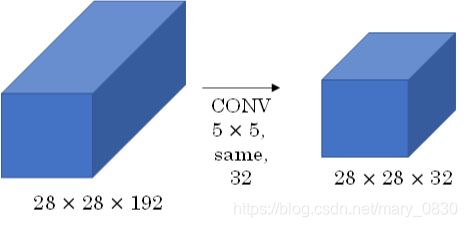
此时的计算量为: 28 ∗ 28 ∗ 32 ∗ 5 ∗ 5 ∗ 192 = 120 M 28*28*32*5*5*192=120M 28∗28∗32∗5∗5∗192=120M(million)。
因此,可以使用1×1CONV可以用于减少计算量,如下图所示: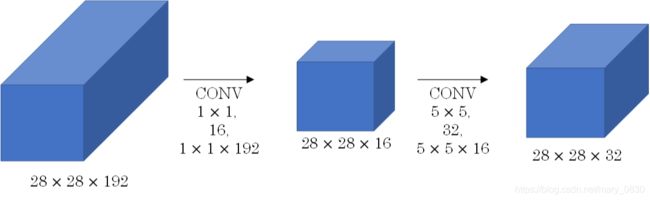
通常1×1CONV称为“瓶颈层”(bottleneck layer)。引入1×1CONV后,此时的计算量为: 28 ∗ 28 ∗ 16 ∗ 192 + 28 ∗ 28 ∗ 32 ∗ 5 ∗ 5 ∗ 16 = 12.4 M 28*28*16*192+28*28*32*5*5*16=12.4M 28∗28∗16∗192+28∗28∗32∗5∗5∗16=12.4M(million)。可见,计算量减少了近90%。
下图是使用了1×1CONV后的Inception 模块:
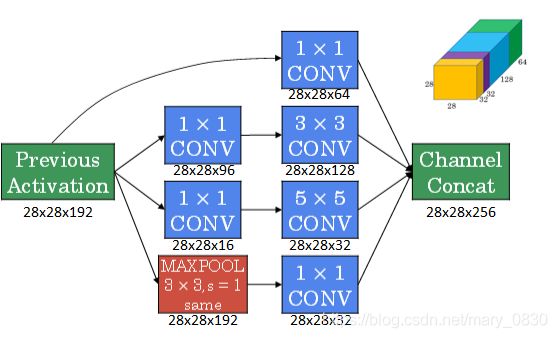
然后,多个Inception模块就组成了Inception网络,如下图所示:
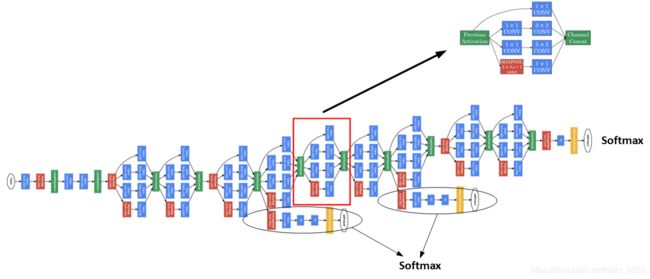
8. 数据增强 Data Augmentation
常用的数据增强方法有:镜像、随意裁剪、颜色变化(颜色扭曲、PCA颜色增强)等。
正如yolov4提到的trick中,关于数据增强的还有图像遮挡、多图组合、自对抗训练等方法,请参考链接。
当构建大型神经网络时,数据增强和训练可以由两个不同的线程来进行。
(上述图片来源)
9. 滑动窗口算法
滑动窗口算法可以使用卷积来实现,作用是提高运行速度,节约计算成本。
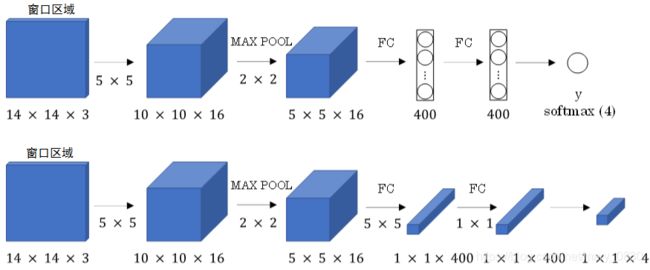
要进行滑动窗口算法,那么就需要把全连接层变成卷积层,具体操作是使用上一层尺寸一致的滤波器算子进行卷积运算即可。
那要是整张图片呢?对于整张图片,就需要使用该网络参数和结构进行计算。比如下图,16 x 16 x 3的输入图片,步长为2,经过CNN得到输出2 x 2 x 4,其中,2 x 2 表示有4个窗口结果。更复杂的输入图片28 x 28 x3,经过CNN得到的输出为8 x 8 x 4。(注意,上面是使用CNN正向进行反复计算的,比如16 x 16 x 3的图片需进行4次,28 x 28 x3的图片需进行64次)
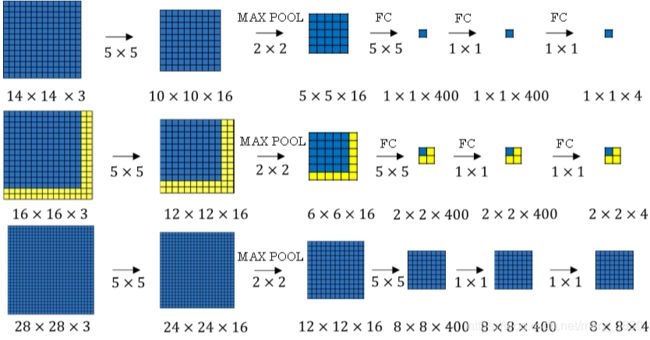
当使用卷积操作代替滑动窗口算法时,不管原始图片有多大,都仅仅一次CNN正向计算即可(因为计算步骤里很多都是共享的),而且窗口的步进长度与Maxpooling的大小有关。
10. 边界框预测 Bounding Box Predictions
滑动窗口算法不能完全框中所有的目标,如下图所示:

为了解决整个问题,提出了YOLO算法,一次性生成多个框进行预测。
具体操作: 将原始图片切割成n x n个网格,每个网格代表一块区域。然后用卷积形式实现滑动窗口算法,对该原始图片构建卷积神经网络,得到输出的维度是3 x 3 x 8,其中,3 x 3 对应的是9个网格,8对应的是每个网格包括8个参数(是否在框内,xywh,类别)。 y = [ P c b x b y b h b w c 1 c 2 c 3 ] y=\begin{bmatrix} P_{c}\\ b_{x}\\ b_{y}\\ b_{h}\\ b_{w}\\ c_{1}\\ c_{2}\\ c_{3}\\ \end{bmatrix} y=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡Pcbxbybhbwc1c2c3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤

P c P_{c} Pc表示目标中心在不在其中的方框内,若是在方框内则 P c = 1 P_{c}=1 Pc=1,否则 P c = 0 P_{c}=0 Pc=0。 b x b_{x} bx和 b y b_{y} by限定在[0,1]内, b w b_{w} bw和 b h b_{h} bh可以大于1,目标可以存在在多个网格内。
11. 交并比 IoU
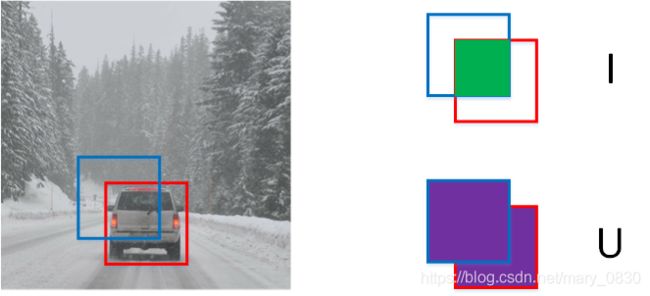
定义: 顾名思义就是交集与并集的比值,用于评价目标检测区域是否准确。
如下图,计算公式: I o U = 绿 色 区 域 紫 色 区 域 IoU =\frac{绿色区域}{紫色区域} IoU=紫色区域绿色区域 ,其中,IoU的数值范围是[0,1]。
12. 非最大抑制 NMS
目标检测算法中,可能会出现很多网格中都检测出了同一个目标的情况,那需要用什么方法来解决这个问题呢?
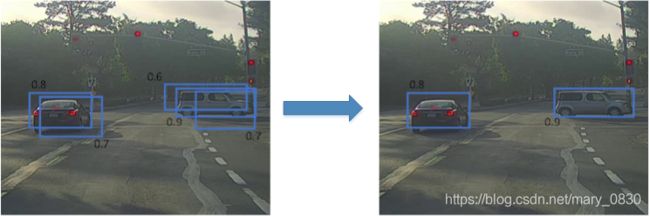
为了解决这个问题,提出了使用NMS(非最大值抑制)的方法,即根据IoU大于某个特定的数值(如0.5,0.6等人为规定的数值)。
对于bbox的表达式来说,即,用 P c P_{c} Pc值的大小来进行NMS。
具体操作是:
- 选取 P c P_{c} Pc中最大的值对应的网格与区域;
- 然后,计算该区域与其他区域的IoU,删掉IoU小于阈值(如0.5)的所有网格与区域;
- 最后,再从留下的网格中选取最大 P c P_{c} Pc值的网格,利用IoU,删掉与该网格交叠较大的网格;
- 重复以上操作,直到找到最后一个最大的网格为止。
13. Anchor Boxes
在目标检测中,Anchor box一般设置有三种尺寸,三种比例(1:1, 1:2, 2:1)。当一个网格中出现两个目标的中心点时,使用不同的Anchor box来检测不同的目标。
使用Anchor box后,则YOLO输出项的表达式变为:
(根据Anchor box的数量改变输出的维度,Anchor boxes之间可以并行实现的) y = [ P c b x b y b h b w c 1 c 2 c 3 P c b x b y b h b w c 1 c 2 c 3 ] y=\begin{bmatrix} P_{c}\\ b_{x}\\ b_{y}\\ b_{h}\\ b_{w}\\ c_{1}\\ c_{2}\\ c_{3}\\ P_{c}\\ b_{x}\\ b_{y}\\ b_{h}\\ b_{w}\\ c_{1}\\ c_{2}\\ c_{3}\\ \end{bmatrix} y=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡Pcbxbybhbwc1c2c3Pcbxbybhbwc1c2c3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
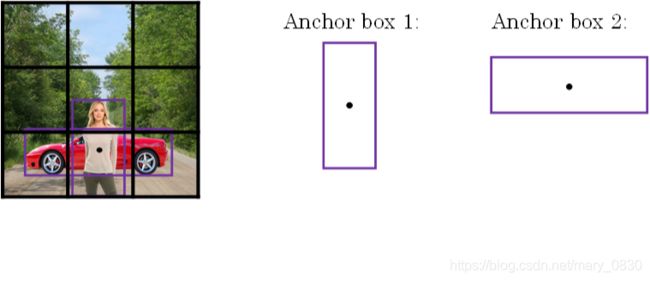
Anchor box和bbox有什么不同呢?
Anchor box可以同时检测重叠的目标,bbox只能检测单个目标。
14. RPN网络
RPN网络是用于二阶段网络的。
首先,提取出候选区域,然后,根据候选区域对目标进行回归与分类的预测。
(上述图片来源)
15. add和concat的不同
add:保证tensor的通道数不变,特征图相加
concat:通道数相加,特征图不变。