蓝桥杯复习——广度优先搜索总结

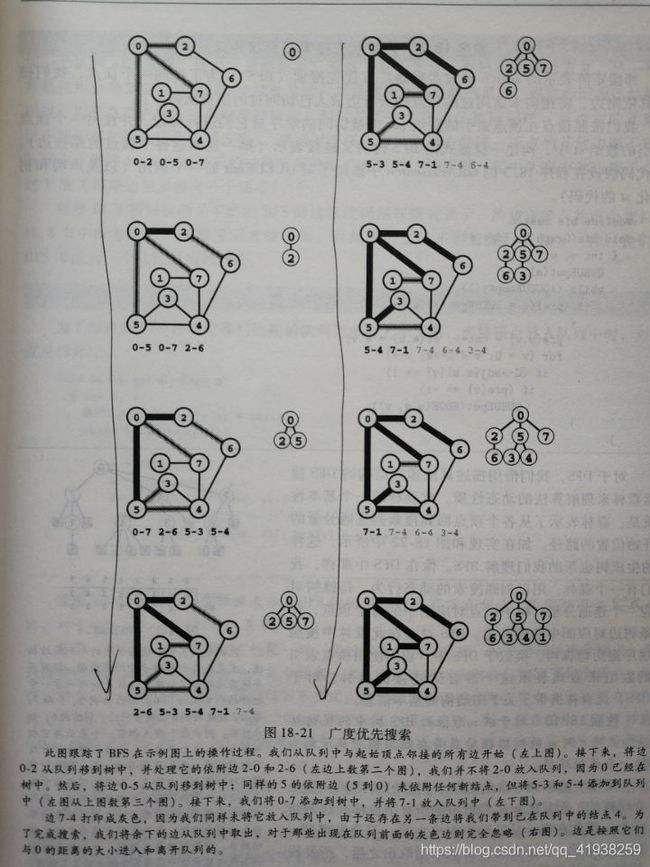
前些日子在刷DFS（深度优先搜索）的题目，而最近在练习BFS（广度优先搜索），现在我对我这一段时间的学习做个总结。BFS类似于树的层次遍历，而DFS则是类似树的先根遍历。我拍了《算法C实现》这本书的讲解，作为BFS的示意图，看的顺序是从上到下，从左到右，如下所示：

BFS会使用到队列这个数据结构，队列是一个先进先出的数据结构。队列是作为一个缓冲区而存在的。先将当前遍历的节点弹出队列，再将所有与他连通的下一跳入队，以此为循环直到队列为空，则遍历结束，这张图的遍历顺序如下所示。

1. 以这张图为例，先将0入队，再将其连通的所有下一跳（2、5、7）分别入队，再将0弹出，此时队列里是257，2为队头，7为队尾。
2. 将2的所有连通下一跳入队（6)，再将2弹出队，此时是576。
3. 再将5的下一跳入队（3、4），再将5弹出队，此时队列里是7634。
4. 将7的下一跳入队（1），4不入队因为已经入过了。
5. 此时全部入队完成，逐一将对里的元素出队到空队为止。

---

依照这个可以写出如下的代码：

#include 
#include
using namespace std;

vector Adj[1000];//建立邻接表存放点的连通信息，当然也可以使用二维数组
int n;//顶点数
bool flag[1000] = { false };//标记是否入过队列，false没有，true则是入了队的

void bfs(int u)
{
    queueq;
    //入队
    q.push(u);
    //入队就标记
    flag[u] = true;
    //循环入队、出队
    while (!q.empty())
    {
        //先取出队头元素再出队
        int u = q.front();
        q.pop();
        //遍历队头元素的所有没入过队的下一跳
        //循环入队操作
        for (int i = 0; i < Adj[u].size(); i++)
        {
           //取出下一跳
            int v = Adj[u][i];
            //没有入过队的才可以入队
            if (flag[v] == false)
            {
                q.push(v);
                flag[v] = true;
            }
        }
    }
}

int main(void)
{
    //实际功能部分
    return 0;
}

---

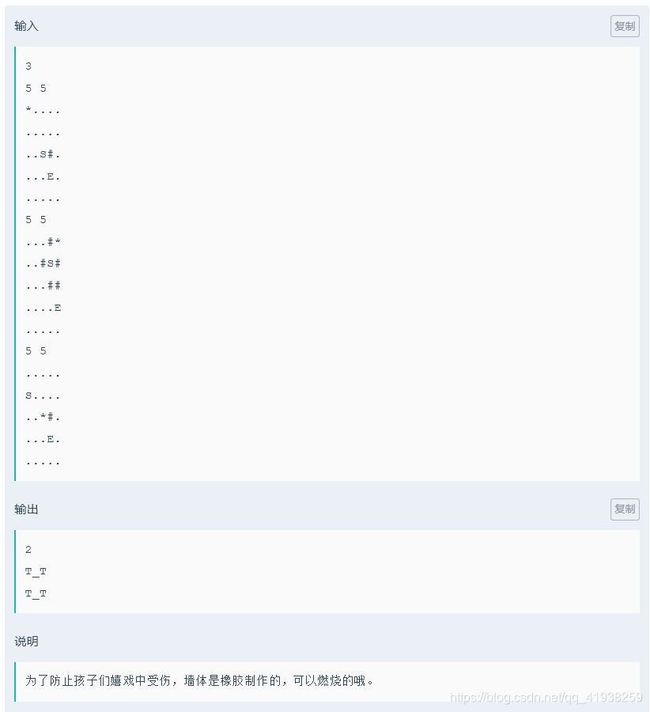
如果要求最小路径的话，看这题：

给出BFS代码：

#include
#include
#include
#include
#include
using namespace std;

struct node
{
    int x, y;
    int step;
}S,E,fire,Node;

bool flag;
bool testunit[35][35];
int n, m;
char map[35][35];
int dr[4] = { -1, 0, 1, 0 };
int dc[4] = { 0, 1, 0, -1 };

float distance(int x1, int y1, int x2, int y2)
{
    return sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));
}  

bool test(int x, int y)
{
    if (x < 0 && x >= n && y < 0 && y >= m)return false;
    if (testunit[x][y] == true)return false;
    if (map[x][y] == '#')return false;
    return true;
}

  

int bfs()
{
    queue Q;
    Q.push(S);

    while (!Q.empty())
    {
        node top = Q.front();
        Q.pop();
        if (top.x == E.x && top.y == E.y)return top.step;


        for (int i = 0; i < 4; i++)
        {
            int X = top.x + dr[i];
            int Y = top.y + dc[i];
            if (test(X, Y))
            {
                Node.x = X;
                Node.y = Y;
                Node.step = top.step + 1;
                Q.push(Node);
                testunit[X][Y] = true;
            }
        }
    }

    return -1;
}
  

int main(void)
{
    memset(testunit, false, sizeof(testunit));
    memset(map, '#', sizeof(map));
    int N;
    cin >> N;
    for (int k = 0; k < N; k++)
    {
        flag = false;
        cin >> n >> m;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
            {
                char temp;
                cin >> temp;
                map[i][j] = temp;
                if (map[i][j] == 'E') { E.x = i; E.y = j; }
                if (map[i][j] == 'S') { S.x = i; S.y = j; }
                if (map[i][j] == '*') { fire.x = i; fire.y = j; }
            }
        int result = -1;
        if (distance(E.x, E.y, S.x, S.y) < distance(fire.x, fire.y, E.x, E.y))
        {
            result = bfs();
        }
        testunit[S.x][S.y] = true;
        if (result == -1)cout << "T_T" << endl;
        else cout << result << endl;
    }

    system("pause");
    return 0;
}

 当然太暴力了没有任何优化是AC不了的，可以看下面这个代码是可以AC的。

#include
#include
#include
using namespace std;

int n, m;
int dir[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };
char mp[31][31];
int vis[31][31], f[31][31];

struct node
{
    int x;
    int y;
    int step;
};

int sx, sy, fx, fy;
queueq;

void bfs(int x, int y)
{
    queueq;
    node a, b, temp1, temp2;
    a.x = x;
    a.y = y;
    a.step = 0;
    q.push(a);

    while (!q.empty())
    {
        a = q.front();
        q.pop();
        //满足条件时
        if (mp[a.x][a.y] == 'E')
        {
            cout << a.step << endl;
            return;
        }

        //这一步是用来简化复杂度的，是回溯算法，
        //满足条件的话说明当前循环以前已经运行过了，就跳过当前这一循环。
        if (f[a.x][a.y] == a.step) continue;
        for (int i = 0; i < 4; i++)
        {
            //初始化b，其意义不是把a拷贝给b
            b = a;
            //遍历下一格
            b.x = a.x + dir[i][0];
            b.y = a.y + dir[i][1];
            //这一步好像有点累赘，但是可以看出是用来下面判断是否满足遍历的条件的
            int xx = b.x;
            int yy = b.y;
            //当前加一步
            b.step += 1;
            //遍历下一格子
            if (mp[xx][yy] != '#' && b.step <= f[xx][yy] && !vis[xx][yy] && xx > 0 && xx <= n && yy > 0 && yy <= m)
            {
                q.push(b);
                vis[xx][yy] = 1;
            }
        }
    }
    //不满足条件时
    cout << "T_T" << endl;
    return;
}

int main()
{
    int t;
    cin >> t;

    while (t)
    {
        while (!q.empty()) q.pop();
        memset(vis, 0, sizeof(vis));
        cin >> n >> m;

        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                cin >> mp[i][j];
                if (mp[i][j] == 'S')
                {
                    sx = i;
                    sy = j;
                }
                if (mp[i][j] == '*')
                {
                    fx = i;
                    fy = j;
                }
            }
        }
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
            {
                f[i][j] = max(abs(fx - i), abs(fy - j));
            }
        vis[sx][sy] = 1;
        bfs(sx, sy);
        t = t - 1;
    }
}

---

END