Kruskal与并查集
Kruskal
(本文中的图片来源于CSDN博友,图中有水印)
作用:构成最小生成树
说明:需要用到并查集算法来优化判断回路的过程,相较与Prim,算法稍微复杂但编程相对简单,在稀疏图中更优越
算法:
【Kruskal】
1.将图中所有的边长权值按从小到大的顺序排列,从小的开始选取边:
①如果发现连上会形成环, 放弃这条边,继续寻找下一个边
②如果发现连上不会成环,连接这条边,并且将这条边两侧的点放入到“已连接”集合中,继续寻找下一个边
2.重复步骤1,直到所有的点都在“已连接”集合中,结束。
【并查集】
1.对于每一次连接,找需要连接的两个点的祖先(爸爸的爸爸的爸爸....)直到找到他们的最先的祖先,比较,如果一样,说明已经连通,不能连接,否则说明可以连接
2.对于每一次成功的连接,后加入“已连接”集合的,都认他所连接的那个已经在集合内的点叫做“爸爸”,如果两个点都是第一次进集合,那么随便认一个点做“爸爸”
3.对于每一次成功的连接,如果是两个家族连接在一起,那么其中一个家族的最先祖先,认另外一个家族的最先祖先做爸爸
可见,只要最先祖先相同,连接起来一定成环
操作:
首先是排序,自行找方法解决即可
但是如何判断有无环呢?难道深搜?广搜?恐怕效率太低。于是我们需要用到并查集算法。
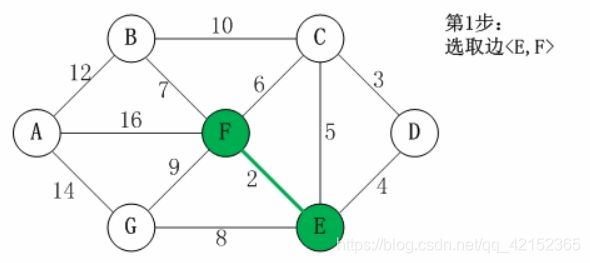
1.首先,找最小权值的边EF,连接起来
已连接集合:{EF}
此时,F是{EF}的最先祖先
2. 然后是CD,不会成环,连接起来
已连接集合:{CDEF}
此时,F是{EF}的最先祖先,C是{CD}的最先祖先
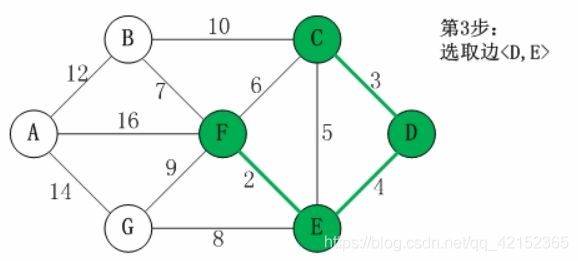
3.然后是DE,不会成环,连接起来
已连接集合:{CDEF} (没变)
此时,{EF}与{CD}合并,{EF}的最先祖先变成C(因为F认C做爸爸了),现在C是{CDEF}的最先祖先
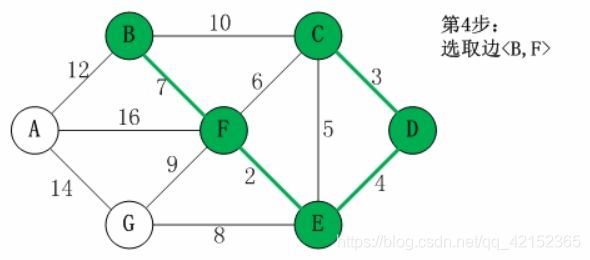
4. 然后是CE,但是C、E的最先祖先都是C,所以CDE成环,所以放弃,同样CF也成环,放弃,找到BF,不成环(每个点初始的最先祖先都是自己),连接起来
已连接集合:{BCDEF}
此时,C是{BCDEF}的最先祖先
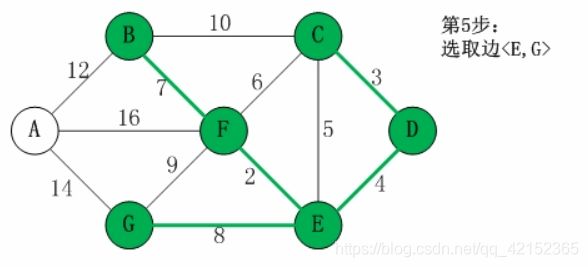
5. 接下来是GE,不成环,连接起来
已连接集合:{BCDEFG}
此时,G是{BCDEFG}的最先祖先
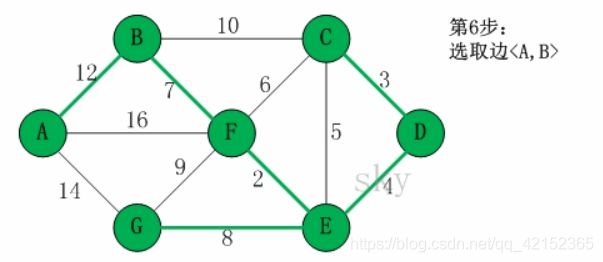
6.随后的FG,BC都是会成环,所以放弃,连接AB,不成环
已连接集合:{ABCDEFG}
全部到齐,不需要再找边了(再找一定成环),故最小生成树如下,C是最先祖先:
值得注意的是,我们一般约定,后进集合的点以及家族成员少的树认先进集合的点以及家族成员多的树做爸爸。
实现:
kruskal()代码:
其中found()为找最先祖先函数,unite为并查集函数
void kruskal()
{
for(int i = 1; i <= m; i++)
{
int x = edge[i].x;
int y = edge[i].y;
if(found(x) != found(y))//两顶点不在一个集合则把该边放入
{
unite(x, y);
ans[c].x = x;
ans[c].y = y;
ans[c].d = edge[i].d;
c++;
}
}
}unite()并查集代码:
其中found()为找最先祖先函数
void unite(int x, int y)
{
int px = found(x);
int py = found(y);
if(px == py)
return;
fa[py] = px;
}found()找最先祖先代码:
int found(int x)
{
if(fa[x] == x)
return x;
else
fa[x] = found(fa[x]);
return fa[x];
}
实战:
https://www.luogu.org/problemnew/show/P2820
该代码有一个测试点未通过(正在努力调试中.....)
#include
#include
using namespace std;
struct edge {
long int left, right;
long int weight;
}map[9999];
bool cmp(edge a, edge b) {
if (a.weight < b.weight) return true;
return false;
}
long int found = 0; //how many points are done
long int price = 0; //how many weights are done
long int total = 0; //total weight for the map
bool judge[9999]; //whther a point is done
long int ptr = 0; //the seq of edges
long int ancestor[9999]; //save the ancestors
long int father(long int son) {
if (ancestor[son] == son) { return son; }
else {
ancestor[son] = father(ancestor[son]);
return ancestor[son];
}
}
void unite(long int a, long int b) {
long int fa = father(a);
long int fb = father(b);
if (fa == fb) { return; }
else { ancestor[fb] = fa; }
return;
}
int main() {
long int n, k;
cin >> n >> k;
for (long int i = 1;i <= n;i++) { judge[i] = false;ancestor[i] = i; }
while (k--) {
long int left, right, weight;
cin >> left >> right >> weight;
ptr++;
total += weight;
map[ptr].left = left;
map[ptr].right = right;
map[ptr].weight = weight;
}
sort(map + 1, map + ptr + 1, cmp);
for (long int i = 1;i <= ptr;i++) {
if (found == n) { break; }
if (father(map[i].left) == father(map[i].right)) { continue; }
//cout << father(map[i].left) << " --- " << father(map[i].right) << " " << map[i].weight <<" "<