InfoGAN:Interpretable Representation Learning by Information Maximizing GANs论文解读
概述:
InfoGAN是国际神经信息处理系统大会NIPS 2016上的论文,作者来自加州大学伯克利分校和OpenAI团队的研究人员,被OpenAI称为当年的五大突破之一。针对传统生成对抗网络以高度混杂的模式使用随机噪声![]() ,随机噪声
,随机噪声![]() 的每一个维度不能显式地表示真实数据空间下的属性或特征的问题,论文所提出的InfoGAN以无监督方式学习隐空间下非混杂方式真实特征表示(disentangled representations)。
的每一个维度不能显式地表示真实数据空间下的属性或特征的问题,论文所提出的InfoGAN以无监督方式学习隐空间下非混杂方式真实特征表示(disentangled representations)。
论文地址:https://arxiv.org/abs/1606.03657
源码地址:https://github.com/openai/InfoGAN、https://github.com/JonathanRaiman/tensorflow-infogan
预备知识:
(1)互信息(Mutual Information)
互信息信息论中衡量随机变量![]() 所包含随机变量
所包含随机变量![]() 的信息量,也就是衡量当随机变量
的信息量,也就是衡量当随机变量![]() 被观察后随机变量
被观察后随机变量![]() 减少的不确定性。互信息可以表示为两个信息熵的差形式:
减少的不确定性。互信息可以表示为两个信息熵的差形式:
![]()
当两个随机变量![]() 和
和![]() 相互独立时,互信息
相互独立时,互信息![]()
(2)信息熵(Entropy)
根据Boltzmann's H-theorem把随机变量![]() (可能值为
(可能值为![]() )的熵定义为:
)的熵定义为:
![]()
当样本数量有限时,熵也可以表示为
其中,![]() 为随机变量
为随机变量![]() 的自信息(信息量),也是一个随机变量
的自信息(信息量),也是一个随机变量
(3)期望(Expectation)
X是离散型的随机变量,可能值为![]() ,对应的概率值为
,对应的概率值为![]() ,概率和为1,
,概率和为1,
研究背景:(Why)
传统的生成对抗网络以高度混杂的模式使用随机噪声![]() ,即使是该网络的构建者也并不能明确的知道随机噪声
,即使是该网络的构建者也并不能明确的知道随机噪声![]() 的每个维度分别对应真实数据的那个属性特征,即
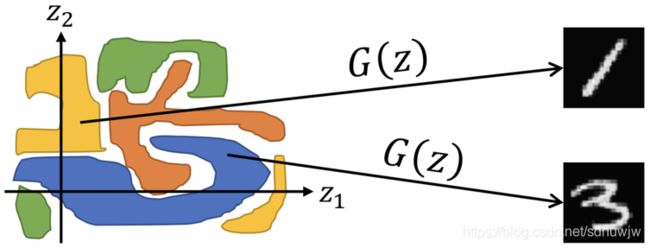
的每个维度分别对应真实数据的那个属性特征,即![]() 随机噪声可解释性差。以MNIST为例,我们并不知道随机噪声的哪一个部分能对应生成数字1或3,如下图所示:
随机噪声可解释性差。以MNIST为例,我们并不知道随机噪声的哪一个部分能对应生成数字1或3,如下图所示:
(图片来源:https://www.slideshare.net/ShuheiYoshida2/infogan-interpretable-representation-learning-by-information-maximizing-generative-adversarial-nets-71376199)
而我们希望能够对潜在空间下的随机噪声进行有序地拆解,使其不同的维度能够代表真实数据空间下不同的显著数据(如数字的宽度、高度、角度等),如下图所示。
(图片来源:https://www.slideshare.net/ShuheiYoshida2/infogan-interpretable-representation-learning-by-information-maximizing-generative-adversarial-nets-71376199)
那么如何通过非监督学习方式获取这些可分解的特征就是InfoGAN所要解决的关键科学问题。
论文核心:用于引导(inducing)潜编码的互信息(What)
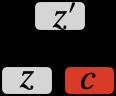
针对传统生成对抗网络未充分利用输入随机噪声的不同维度的特征表示能力,InfoGAN将随机噪声分为两部分(如下图所示):
(1)不可压缩部分![]() ;
;
(2)可解释的隐编码![]() :对应真实数据分布下显著的语义特征(如:MNIST数字的宽度、高度、角度等):
:对应真实数据分布下显著的语义特征(如:MNIST数字的宽度、高度、角度等):
因此,InfoGAN的生成器可以表示为![]() ,通过最大化潜编码
,通过最大化潜编码![]() 与生成数据
与生成数据![]() 之间的互信息来防止生成对抗网络在训练过程中忽略隐编码
之间的互信息来防止生成对抗网络在训练过程中忽略隐编码![]() 的特征表示能力。因为潜编码
的特征表示能力。因为潜编码![]() 和生成数据
和生成数据![]() 之间具有较高的相关性,即潜编码
之间具有较高的相关性,即潜编码![]() 的不同维度对应生成数据
的不同维度对应生成数据![]() 的特定的显著性特征,因此它们之间具有较高的互信息
的特定的显著性特征,因此它们之间具有较高的互信息![]() 很高,如下图所示:
很高,如下图所示:
因此,将互信息![]() 作为正则化项的对抗训练目标函数优化为:
作为正则化项的对抗训练目标函数优化为:
![]()
互信息![]() 越大表明潜编码
越大表明潜编码![]() 对生成数据
对生成数据![]() 具有更强大的解释能力,因此,我们希望该互信息
具有更强大的解释能力,因此,我们希望该互信息![]() 越大越好。
越大越好。
但是,在计算互信息![]() 时需要用到真实的后验
时需要用到真实的后验![]() ,因为真实的后验概率
,因为真实的后验概率![]() 是很难采样和估计的。
是很难采样和估计的。
因此,就需要另外一个函数![]() 来近似逼近后验概率
来近似逼近后验概率![]() ,通过变分信息最大化方法来让变分分布
,通过变分信息最大化方法来让变分分布![]() 来逼近真实后验
来逼近真实后验![]() ,从而得到用
,从而得到用![]() 表示的互信息
表示的互信息![]() 的下界。
的下界。
同时,为了简化分析将隐编码![]() 的数据分布固定,其熵
的数据分布固定,其熵![]() 即可视为常数,
即可视为常数,
通过变分信息最大化得到的互信息下界,就可以避免显式地计算后验概率![]() ,
,
但是在内部期望中还存在从后验概率![]() 中采样的问题,因此还需要方法再移除内部期望的后验概率。
中采样的问题,因此还需要方法再移除内部期望的后验概率。
此时,需要根据论文中提到的引理5.1:![]() (论文arXiv版的附录提供对引理的证明,这里不再赘述)来消除内部期望中的后验概率
(论文arXiv版的附录提供对引理的证明,这里不再赘述)来消除内部期望中的后验概率![]() ,即:
,即:
依据引理5.1定义互信息![]() 的变分下界
的变分下界![]() ,以此该变分下界可以利用重构技巧直接通过函数(网络)
,以此该变分下界可以利用重构技巧直接通过函数(网络)![]() 和
和![]() 实现最大化,通过蒙特卡洛模拟可以很容易得逼近。
实现最大化,通过蒙特卡洛模拟可以很容易得逼近。
具体方法:(How)
在大多数试验中都是通过神经网络来构建![]() 网络,同时共享判别器的卷积层,如下图所示,这样也不会增加太多额外的计算成本。
网络,同时共享判别器的卷积层,如下图所示,这样也不会增加太多额外的计算成本。
图中的虚线是计算互信息的原始后验![]() 表示。但是,由于对后验概率
表示。但是,由于对后验概率![]() 采样很难,因此需要通过变分信息最大化方式通过
采样很难,因此需要通过变分信息最大化方式通过![]() 来逼近真实后验
来逼近真实后验![]() ,如图中红色弯曲箭头
,如图中红色弯曲箭头
整个网络的训练在原目标函数的基础上,增加互信息下界![]() ,因此InfoGAN的目标函数最终表示为:
,因此InfoGAN的目标函数最终表示为:
![]()
其中,![]() 取1(离散型c)或者取值为和原始GANs目标函数相同数量级的较小的数值(连续性c)
取1(离散型c)或者取值为和原始GANs目标函数相同数量级的较小的数值(连续性c)
实验:
InfoGAN的试验有两个目标:
(1)验证互信息是否能被有效地最大化
(2)是否能够通过无监督方式学习到可分解、可解释的特征表示(每次变化潜编码的一个维度,验证在生成图像上发生的显著特征改变)
(一)互信息最大化实验
首先,在MNIST数据集上验证,隐编码取值从10个类别中取样,每个类别的概率为0.1的离散数据,试验结果表明InfoGAN的下界能够很快达到最大值2.3
对比对象为传统的GANs仅添加辅助分布![]() ,但是没有明确地使用隐编码来最大化互信息。传统的GANs没有充分利用好隐编码,因此互信息就低。
,但是没有明确地使用隐编码来最大化互信息。传统的GANs没有充分利用好隐编码,因此互信息就低。
(二)非混杂的特征表示实验
![]()
![]()
分解的特征表示试验表明:
(1)隐编码c的第一个维度可以控制生成数字的类别
(2)第二个维度控制生成数字的旋转角度
(3)第三个维度控制生成数字的宽度
总结:
目标:以无监督方式学习可分解的特征表示
方法:生成对抗网络 (GANs) + 最大化生成图片与输入隐编码之间的互信息(MI)
优势:以无监督方式学习随机噪声空间下可解释的特征表示时,无需大量的额外计算成本
参考文献:
[1] Chen X, Duan Y, Houthooft R, et al. Infogan: Interpretable representation learning by information maximizing generative adversarial nets[C]//Advances in neural information processing systems. 2016: 2172-2180.