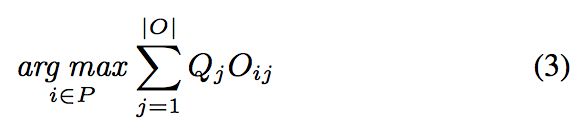Pareto-Efficient Hybridization for Multi-Objective Recommender Systems

ABSTRACT 简介

Performing accurate suggestions is an objective of paramount importance for effective recommender systems. Other important and increasingly evident objectives are novelty and diversity, which are achieved by recommender systems that are able to suggest diversified items not easily discovered by the users. Different recommendation algorithms have particular strengths and weaknesses when it comes to each of these objectives, motivating the construction of hybrid approaches. However, most of these approaches only focus on optimizing accuracy, with no regard for novelty and diversity. The problem of combining recommendation algorithms grows significantly harder when multiple objectives are considered simultaneously. For instance, devising multi-objective recommender systems that suggest items that are simultaneously accurate, novel and diversified may lead to a conflicting-objective problem, where the attempt to improve an objective further may result in worsening other competing objectives. In this paper we propose a hybrid recommendation approach that combines existing algorithms which differ in their level of accuracy, novelty and diversity. We employ an evolutionary search for hybrids following the Strength Pareto approach, which isolates hybrids that are not dominated by others (i.e., the so called Pareto frontier). Experimental results on two recommendation scenarios show that: (i) we can combine recommendation algorithms in order to improve an objective without significantly hurting other objectives, and (ii) we allow for adjusting the compromise between accuracy, diversity and novelty, so that the recommendation emphasis can be adjusted dynamically according to the needs of different users.

对于推荐系统来说，进行准确的推荐是至关重要的目标。另一个日益重要的目标是新颖性和多样性，多样性是通过推荐系统来达成的，推荐系统能够推荐用户不易发现的多样性物品。不同的推荐算法在实现每一个目标时都有其独特的优势和弱点，从而推动了混合方法的构建。然而，这些方法大多只注重优化精度，而不考虑新颖性和多样性。当同时考虑多个目标时，组合推荐算法变得更加困难。例如，设计多目标推荐系统，同时推荐准确、新颖和多样化的物品，可能会导致目标冲突问题，提升某个目标可能会导致其他竞争目标恶化。本文提出了一种混合推荐方法，该方法结合了现有算法的准确性、新颖性和多样性。我们采用强度帕累托方法对杂交种进行进化搜索，分离出不受其他杂交种支配的杂交种（即所谓的帕累托前沿）。在两种推荐场景下的实验结果表明：（1）我们可以将推荐算法结合起来，在不显著损害其他目标的情况下提升某个目标；（2）我们可以调整准确性、多样性和新颖性之间的折衷，从而根据不同用户的需求动态调整推荐应该强化哪个目标。

1. INTRODUCTION 概述

Recommender systems are increasingly emerging as enabling mechanisms devoted to overcoming problems that are inherent to information overload, providing intelligent information access and delivery, and thus potentially improving browsing and consumption experience. Historically, the typical goal of a recommender system is to maximize accuracy as much as possible in predicting and matching user information needs, often by considering individual delivered items in isolation [12]. More recently, however, it has become a consensus that the success of a recommender system depends on other dimensions of information utility, notably the diversity and novelty of the suggestions performed by the system [9, 19, 25, 33]. More specifically, even being accurate, obvious and monotonous recommendations are generally of little use, since they do not expose users to unprecedent experiences.

推荐系统正日益成为一种基本机制，致力于克服信息过载所固有的问题，提供智能信息访问和传递，从而可能改善浏览和消费体验。从历史上看，推荐系统的典型目标是尽可能提高预测和匹配用户信息需求的准确性，通常是通过单独考虑单个交付的物品来实现的[12]。然而，最近的一个共识是，推荐系统的成功取决于信息效用的其他方面，特别是系统推荐的多样性和新颖性[9、19、25、33]。更具体地说，过于大众和单调的推荐，即使推荐是准确的，通常也没有多大用处，因为它们不会让用户体验到前所未有的体验。

Increasing novelty and diversity by completely giving up on accuracy is straight forward and meaningless, since the system will not meet the users needs anymore. In fact, there is an apparent trade-off between these dimensions, which becomes evident by inspecting the performance of existing top-N recommendation algorithms. An easy conclusion is that different algorithms may perform distinctly depending on the dimension of interest (i.e., the best performer in terms of accuracy is not the best one in terms of novelty and diversity), and thus it is hard to point to a best performer if all the dimensions are considered simultaneously. A conclusion which is harder to reach is whether these algorithms are indeed complementary, so that the strengths of an algorithm may compensate the weaknesses of others. The potential synergy between different recommendation algorithms is of great importance to multi-objective recommender systems, since they must achieve a proper level of each dimension (i.e., objective).

完全放弃精确性来增加新颖性和多样性是毫无意义的，因为系统将不再满足用户的需求。事实上，这些维度之间存在明显的折衷，通过研究现有top-N推荐算法的表现可以明显看出这一点。一个简单的结论是，不同的算法可以明显地根据感兴趣的维度来执行（即，一个算法无法同时在准确性、新颖性和多样性方面表现最好），因此，如果同时考虑所有维度，很难指出表现最好的算法。一个更难得出的结论是，这些算法是否真的是互补的，因此一个算法的优点可以弥补其他算法的缺点。不同推荐算法之间的协同作用对于多目标推荐系统来说是非常重要的，因为它们必须达到每个维度（即目标）的适当水平。

In this paper we hypothesize that it is possible to properly aggregate different recommendation algorithms, so that the resulting hybrids balances the level of accuracy, diversity and novelty in its suggestions. In this case, each potential hybrid is given as a weighted combination of well-established recommendation algorithms (e.g., simple algorithms as well as representative of the state-of-the-art). Our proposed hybridization approach consists in finding appropriate weights for the constituent algorithms. By considering each dimension (i.e., accuracy, novelty and diversity) as a separate objective, we reduce the hybridization task to a multi-objective optimization problem, in which we search for the optimal combination of weights that maximizes accuracy, diversity and novelty.

在本文中，我们假设可以适当地聚合不同的推荐算法，从而使产生的混合算法在其推荐的准确性、多样性和新颖性方面达到平衡。在这种情况下，每一个潜在的混合体都是作为一个已有推荐算法（例如，简单算法以及最新技术的代表）的加权组合给出的。我们提出的混合方法是为组成算法寻找合适的权重。将每个维度（准确性、新颖性和多样性）作为一个独立的目标，将混合任务简化为一个多目标优化问题，在该问题中，我们寻找权重的最佳组合，以使准确性、多样性和新颖性最大化。

Since the considered objectives are potentially conflicting, we employ an evolutionary search for optimal hybrids. Evolutionary algorithms denote a class of optimization methods that are characterized by a set of candidate solutions (aka individuals) called a population, which is maintained during the entire optimization process. The population of individuals evolves towards better (and potentially optimal) solutions by employing genetic operators, such as reproduction, mutation and crossover. In our context, each individual represents a possible combination of weights (i.e., a possible hybrid). Optimal hybrids lie in the so-called Pareto frontier [37], and are optimal in the sense that no hybrid in the frontier can be improved upon without hurting at least one of its objectives. Therefore, the evolutionary algorithm evolves the population towards producing hybrids that are located closer to the Pareto frontier, and then a linear search returns the most dominant hybrid [37], which is likely to balance accuracy, novelty and diversity. Alternatively, hybrids in the Pareto frontier can be selected according to a certain need, allowing the recommender system to adjust the compromise between accuracy, novelty and diversity, so that the recommendation emphasis can be adapted dynamically according to the needs of each user (i.e., new users may benefit more from more accurate suggestions, whereas older users may require more novel and diversified suggestions).

由于这些目标是潜在冲突的，我们采用进化搜索来优化混合推荐。进化算法是指在整个优化过程中以一组称之为种群的候选解（即个体）为特征的优化方法。种群通过使用遗传算子，如繁殖、变异和交叉，向更好（和潜在最优）的解决方案进化。就我们而言，每个个体代表可能的权重组合（即，可能的混合）。最优群体存在于所谓的帕累托前沿[37]，并且是最优的，因为帕累托前沿的群体在不损害其至少一个目标的情况下是无法改进的。因此，进化算法将种群进化为更靠近帕累托前沿的群体，然后线性搜索返回最主要的混合体[37]，这可能平衡准确性、新颖性和多样性。或者，帕累托前沿的混合体可以根据特定的需要进行选择，使得推荐系统能够调整准确性、新颖性和多样性之间的折衷，从而可以根据每个用户的需要动态地调整推荐重点（即，新用户可能会从更准确的推荐中受益，而老用户可能需要更新颖和多样化的推荐）。

We conducted a systematic evaluation involving different recommendation scenarios, with explicit user feedback (i.e., movies from the MovieLens dataset), as well as implicit user feedback (i.e., artists from the LastFM dataset). The experiments showed that it is possible to (i) combine different algorithms in order to produce better recommendations and (ii) control the desired balance between accuracy, novelty and diversity. In order to evaluate the baseline algorithms and our hybrids, we used the methodology for top-N evaluation proposed in [12] and measured novelty and diversity using the framework proposed in [33].

我们对不同的推荐场景进行了系统的评估，包括明确的用户反馈（即来自MovieLens数据集的电影）和隐含的用户反馈（即来自LastFM数据集的艺术家）。实验表明，我们可以：（i）将不同的算法结合起来以产生更好的推荐，以及（ii）在准确性、新颖性和多样性之间控制所需的平衡是可能的。为了评估基线算法和我们的混合算法，我们使用了[12]中提出的top-N评估方法，并使用[33]中提出的框架测量新颖性和多样性。

 

2. PRELIMINARIES 预备知识

In this section we review the main concepts about evolutionary algorithms and multi-objective optimization. Finally, we discuss related work on hybrid and multi-objective recommender systems.

在这一部分，我们回顾了进化算法和多目标优化的主要概念。最后，讨论了混合多目标推荐系统的相关工作。

2.1 Evolutionary Algorithms 进化算法

Evolutionary algorithms are meta-heuristic optimization techniques that follow processes such as inheritance and evolution as key components in the design and implementation of computer-based problem solving systems [15, 20]. In evolutionary algorithms, a solution to a problem is represented as an individual in a population pool. The individuals may be represented as different data structures, such as vectors, threes, or stacks [26]. If the individual is represented as a vector, for example, each position in the vector is called a gene.
Typically, evolutionary algorithms employ a training and a validation set, as described in Algorithm 1. Initially, the population starts with individuals created randomly (line 6). The evolutionary process is composed of a sequence of solution generations. The process evolves generation by generation through genetic operations (lines 7-12). The goal of this process is to obtain better solutions after some generations. A fitness function is used to assign a fitness value to each individual (line 9), which represents its performance on the training set or in a cross validation set. To produce a new generation, genetic operators are applied to individuals with the aim of creating more diverse and better individuals (line 12). Typical operators include reproduction, mutation, and crossover.

进化算法是继遗传和进化等过程之后的元启发式优化技术，是设计和实现基于计算机的问题解决系统的关键组成部分[15，20]。在进化算法中，问题的解被表示为种群中的个体。个体可以表示为不同的数据结构，例如向量、三纬或堆栈[26]。例如，如果个体被表示为一个向量，那么向量中的每个位置都称为一个基因。

通常，进化算法采用训练和验证集，如算法1所述。最初，种群是从随机创建的个体开始的（第6行）。进化过程是由一系列的解生成过程组成的。这个过程通过遗传操作一代一代地进化（第7-12行）。这个过程的目标是在几代人之后获得更好的解决方案。fitness函数用于为每个个体（第9行）分配一个fitness值，该值表示其在训练集或交叉验证集中的性能。为了产生新一代，遗传算子被应用于个体，目的是创造更多样化和更好的个体（第12行）。典型的操作包括复制、变异和交叉。

2.2 Multi-Objective Optimization 多目标优化

Since we are interested in maximizing three different objectives for the sake of recommender systems (i.e. accuracy, novelty, and diversity), we use a multi-objective evolutionary algorithm. In multi-objective optimization problems there is a set of solutions that are superior to the remainder when all the objectives are considered together. In general, traditional approaches to multi-objective optimization problems are very limited because they become too expensive as the size of the problem grows [8]. Multi-objective evolutionary algorithms are a suitable option to overcome such an issue. Typically, multi-objective evolutionary algorithms are classified as Pareto or non-Pareto [37]. In the non-Pareto optimization case, the objectives are combined into a single evaluation value that is used as fitness value (i.e., average of the objectives). In Pareto algorithms, on the other hand, a vector of objective values is used (i.e., the individual is given as an objective vector). The evaluation of Pareto approaches follows the Pareto dominance concept. An individual dominates another if it performs better in at least one of the objectives considered. Given two arbitrary individuals, the result of the dominance operation has two possibilities: (i) one individual dominates another, or (ii) the two individuals do not dominate each other. An individual is denoted as non-dominated if it is not dominated by any other individual in the population, and the set of all non-dominated individuals compose the Pareto frontier.

由于我们感兴趣的是最大化推荐系统的三个不同目标（准确性、新颖性和多样性），所以我们使用了一种多目标进化算法。在多目标优化问题中，当所有目标同时考虑时，存在一组解优于其他解。一般来说，传统的多目标优化方法是非常有限的，因为随着问题规模的增长，它们耗费的资源过多[8]。多目标进化算法是解决这一问题的一种有效方法。通常，多目标进化算法分为Pareto算法和非Pareto算法[37]。在非帕累托算法中，目标被组合成一个单独的评价值，作为适应度值（即目标的平均值）。另一方面，在Pareto算法中，使用了一个目标值向量（即，将个体作为目标向量给出）。帕累托方法的评估遵循帕累托支配的概念。如果一个个体在所考虑的目标中至少有一个表现得更好，他就会支配另一个个体。给定两个任意的个体，支配操作的结果有两种可能性：（i）一个个体支配另一个个体，或（ii）两个个体互不支配对方。如果一个个体不受任何其他个体的支配，那么它就被称为非支配个体，所有非支配个体的集合构成帕累托边界。

In this work we use a second version of the strength Pareto evolutionary algorithm (SPEA-2) [36, 37]. The aim is to find or approximate the Pareto-optimal set for multi-objective problems. The main features of this algorithm are: (i) the fitness assignment scheme takes into account how many individuals each individual dominates or is dominated by, (ii) it uses a nearest neighbour density estimation technique to break ties in solutions with the same fitness, (iii) the size of the population of non-dominated solutions is a fixed value η. Thus, we have two situations. First, when the actual number of non-dominated solutions is lower than η, the population is filled with dominated solutions; second, when the actual number of non-dominated solutions exceeds η, some of them are discarded by a truncation operator which preserves boundary conditions, even though we always keep the current Pareto Frontier in a list separate from the population, so we can later retrieve the individuals in it.

在这项工作中，我们使用第二个版本的强度帕累托进化算法（SPEA-2）[36，37]。目的是寻找或逼近多目标问题的Pareto最优集。该算法的主要特点是：（i）适应度分配方案考虑了每个个体支配或被支配的个体数量；（ii）它使用最近邻密度估计技术来打破具有相同适应度的解之间的联系；（iii）非支配解的总体大小是一个固定值 η。因此，我们有两种情况。第一，当非支配解的实际个数小于η时，种群中全为支配解；第二，当非支配解的实际个数超过η时，其中一些被保留边界条件的截断算子丢弃，不过，我们总是将当前的Pareto边界保持在一个单独的列表中，这样我们以后就可以找到其中的个体。

 

2.3 Related Work 相关工作

Traditionally, hybrid recommender strategies are the combination of two different families of algorithms, namely, content-based and collaborative filtering [1]. In this work, we combine many (up to 8) recommendation algorithms - different content-based and collaborative filtering algorithms that deal with explicit and implicit feedback, etc. We treat each recommendation algorithm as a black-box, so adding or removing recommendation algorithms is easy. Different hybridization strategies have been proposed to combine recommender methods, such as weighted approaches [10], voting mechanisms [30], switching between different recommenders [6, 24], and re-ranking the results of one recommender with another [7].

传统上，混合推荐策略是两类不同算法的组合，即基于内容的和协同过滤的[1]。在这项工作中，我们结合了许多（最多8个）推荐算法-不同的基于内容的和处理显式和隐式反馈的协同过滤算法等。我们将每个推荐算法视为一个黑箱，因此添加或删除推荐算法很容易。人们提出了不同的混合策略来组合推荐方法，例如加权方法[10]、投票机制[30]、在不同推荐方法之间切换[6、24]，以及将一个推荐的结果与另一个推荐的结果重新排序[7]。

A prominent use of hybridization in recommender systems is the Belkor system that won the Netflix competition [4, 5]. Their method is a statically weighted linear combination of 107 collaborative filtering engines. There are important differences between their work and ours: (i) their solution is single-objective (accuracy), (ii) they combine only collaborative filtering information, and (iii) the recommendation task is rating prediction, focused on RMSE - which makes the aggregation simpler, since all of the ratings are on the same scale and consist of the same items.

在推荐系统中，混合推荐的一个突出应用是赢得Netflix竞争的Belkor系统[4，5]。他们的方法是107个协同过滤引擎的静态加权线性组合。他们的工作和我们的工作有着重要的区别：（i）他们的解决方案是单目标（准确度），（ii）他们只结合了协同过滤信息，和（iii）他们的推荐任务是评级预测，重点是RMSE-这使得聚合更简单，因为所有评级都在同一个尺度上，有同样的物品。

There has been an increasing consensus in the recommender systems community about the importance of proposing algorithms and methods to enhance novelty and diversity [17, 33]. As showed in [35], user satisfaction does not always correlate with high recommender accuracy. Thus, different multi-objective algorithms have been proposed to improve user experience considering either diversity or novelty. For instance, in [35], the authors define a greedy re-ranking algorithm that diversifies baseline recommendations. Another approach to improve diversity is presented in [34], where they suggest an optimization method to improve two objective functions reflecting preference similarity and item diversity.

对于提出算法和方法以增强新颖性和多样性的重要性，推荐系统界已经有了越来越多的共识[17，33]。如[35]所示，用户满意度并不总是与推荐的高准确度相关。因此，考虑到用户体验的多样性和新颖性，人们提出了不同的多目标算法来改善用户体验。例如，在[35]中，作者定义了一个贪婪的re-ranking算法，该算法使基线推荐多样化。文献[34]提出了另一种改进多样性的方法，他们提出了一种优化方法来改进反映偏好相似性和物品多样性的两个目标函数。

On the other hand, novelty has been understood as recommending long-tail items, i.e., those items which few users have accessed. In [33], the authors present hybrid strategies that combine collaborative filtering with graph spreading techniques to improve novelty. The authors in [9] take an alternative approach: instead of assessing novelty in terms of the long-tail items that are recommended, they follow the paths leading from recommendations to the long tail using similarity links. As far as we know, this is the first work that proposes a hybrid method that is multi-objective in terms of the three metrics, i.e., accuracy, diversity and novelty.

另一方面，新颖性被理解为推荐长尾物品，即那些很少有用户访问过的物品。在[33]中，作者提出了混合策略，将协同过滤与图形扩展技术相结合，以提高新颖性。[9]中的作者采用了另一种方法：他们不根据推荐的长尾物品来评估新颖性，而是使用相似链接进行长尾推荐。据我们所知，这是第一次提出一种多目标的混合方法，即精确性、多样性和新颖性。

Extensive research has also been performed exploiting the robust characteristics of genetic algorithms in recommender systems. For instance, in [28] the authors build a content-based recommender system and use genetic algorithms to assign proper weights to the words. Such weights are combined using the traditional IR vector space model [2] to produce recommendations. In [23] the authors use a genetic algorithm to build a recommender method that considers the browsing history of users in real-time. In contrast to our approach (which uses a GA to combine multiple recommender methods), they use GA to build a single-method.

对遗传算法在推荐系统中的鲁棒特性，也有广泛的研究。例如，在[28]中，作者建立了一个基于内容的推荐系统，并使用遗传算法为单词分配适当的权重。使用传统的IR向量空间模型[2]组合这些权重以进行推荐。在文献[23]中，作者使用遗传算法建立了一种实时考虑用户浏览历史的推荐方法。与我们的方法（使用遗传算法组合多个推荐方法）不同，他们使用遗传算法构建单个方法。

In [22], the authors present an implementation of GA for optimal feature weighting in the multi-criteria scenario. Their application of GA consists in selecting features that represent users’ interest in a collaborative filtering context, in contrast to our method, which focuses on assigning weights to different recommendation algorithms in order to improve the overall performance in terms of accuracy, novelty and diversity.

在文献[22]中，作者提出了一种在多准则情形下的最优特征加权遗传算法的实现。它们的应用是在协同过滤环境中选择代表用户兴趣的特征，与我们的方法不同，我们的方法侧重于为不同的推荐算法分配权重，以便在准确性、新颖性和多样性方面提高整体性能。

 

3. PARETO-EFFICIENT HYBRIDIZATION

In this section we introduce our search approach for Pareto-Optimal hybrids. We start by discussing how different recommendation algorithms are combined, so that potential hybrids are created. Then we describe the evolutionary search for Pareto-Optimal hybrids. Finally, we discuss an approach to deal with the compromise between accuracy, novelty and diversity, so that the system is able to adjust itself for different user perspectives.

在这一节中，我们介绍了我们的帕累托最优混合搜索方法。我们首先讨论如何组合不同的推荐算法，以便创建潜在的混合算法。然后我们描述了Pareto最优混合的进化搜索。最后，我们讨论了一种在准确性、新颖性和多样性之间进行折衷的方法，使系统能够根据不同的用户视角进行自我调整。

3.1 Weighted Hybridization 加权混合

Our hybridization approach is based on assigning weights to each constituent algorithm. We denote the set of constituent algorithms as A and the score given by algorithm Aj for an item i is represented by Aj(i). As the constituent algorithms may output scores in drastically different scales, a simple normalization procedure is necessary to ensure that all algorithms in A operate in the same scale. The aggregated score for each item i is calculated as:

            (1)

where W is a vector that represents the weight assigned to each constituent algorithm. The assignment of weights to each algorithm is formulated as a search problem which we discuss next.

我们的混合方法是基于给每个组成算法分配权重。我们将组成算法集表示为A，并且由算法给出的物品i的得分用表示。由于组成算法可能以完全不同的尺度输出分数，因此需要一个简单的归一化过程来确保A中的所有算法都在相同的尺度下操作。每个物品i的总分计算如下：

            (1)

其中W表示分配给每个组成算法的权重的向量。每个算法的权重分配都被表示为一个搜索问题，我们接下来将讨论这个问题。

 

3.2 Searching for Pareto-Optimal Hybrids 搜索帕累托最优混合

Finding a suitable vector of weights W can be viewed as a search problem in which possible solutions are given as a combination of weights {}, such that each wi is selected in a way that optimizes a established criterion. We consider the application of evolutionary algorithms for searching optimal solutions. These algorithms iteratively evolve a population of individuals towards optimal solutions by performing operations based on reproduction, mutation, recombination, and selection [18]. This approach is interesting because we have no knowledge of the search space, since any number of different algorithms may be used, in different domains. Next, we precisely define an individual.

找到一个合适的权重向量W可以看作是一个搜索问题，在这个问题中，可能的解是权重的组合{}，以优化某个已建立的标准来选择。我们考虑应用进化算法寻找最优解。这些算法通过执行基于复制、变异、重组和选择的操作，迭代地将个体种群进化为最优解[18]。这种方法很有趣，因为我们对搜索空间一无所知，因为在不同的领域中，可能会使用任意数量的不同算法。接下来，我们精确地定义一个个体。

Definition 1: An individual is a candidate solution, which is encoded as a sequence of |A| values [], where each indicates the weight associated with algorithm  ∈ A.
Each algorithm assigns scores to items using a cross-validation set. Finally, weights are assigned to each algorithm and their scores are aggregated according to Equation 1, producing an individual. A fitness function is computed for each individual in order to make them directly comparable, so that the population can evolve towards optimal solutions.

定义1：个体是一个候选解，它被编码为一个有|A|个值的序列[]，其中每个表示与算法∈A相关联的权重。

每个算法使用交叉验证集为物品分配分数。最后，为每个算法分配权重，并根据等式1聚合它们的得分，生成个体。为每个个体计算一个适应度函数，以使它们直接可比，从而使种群进化到最优解。

 

Definition 2: An optimal solution is a sequence of weights W = {}, satisfying:

             (2)

where is a metric used to measure an objective, which can be either accuracy, novelty or diversity. These metrics are better discussed in Section 4. For now it suffices to notice that the performance of each individual is given by a 3-dimensional objective vector, containing the average accuracy, novelty and diversity over the users in the cross validation set ( since different metrics may operate in different scales, we normalize each to the 0-1 interval). Searching for optimal solutions, therefore, is a multi-objective optimization problem, in which the value of must be maximized for each of the 3 objectives that compose an optimal solution. Therefore, multiple optimal individuals are possible. It is worth noticing that different datasets and combinations of algorithms and A will generate different optimal individuals.

定义2：最优解是一个权重序列W={}，该序列满足如下条件：

             (2)

其中，是用于衡量目标的度量，可以是精确性、新颖性或多样性。第4节对这些指标进行了更详细的讨论。现在只需注意，每个个体的性能是由一个三维目标向量给出的，它包含交叉验证集中用户的平均准确性、新颖性和多样性（因为不同的度量可能量纲不同，我们将每个标准化到0-1）。因此，寻找最优解是一个多目标优化问题，在这个问题中，组成最优解的3个目标的值必须最大化。因此，多个最优个体是可能的。值得注意的是，不同的数据集以及算法和A的组合将产生不同的最优个体。

A general strategy for solving a multi-objective optimization problem is to exploit the concept of Pareto dominance, which may be used to find solutions that are not dominated by others. These non-dominated solutions lie in the so-called Pareto frontier, and are optimal in the sense that no solution in the frontier can be improved upon without hurting at least one of its objectives. Therefore, the evolutionary algorithm evolves the population towards producing individuals that are located closer to the Pareto frontier, and then a linear search returns the individual which simply maximizes the average (or some other combination, as we see on the next section) of the three objectives. Under this strategy, we follow the well-known Strength Pareto Evolutionary Algorithm approach [36], which has shown to be highly effective and also because it provides more diverse results when compared to existing approaches [11, 13, 32] for many problems of interest. The Strength Pareto approach isolates individuals that achieve a compromise between maximizing the competing objectives by evolving individuals that are likely to be non-dominated by other individuals in the population.

求解多目标优化问题的一般策略是利用Pareto支配的概念，利用Pareto支配可以找到不受解支配的解。这些非支配解存在于所谓的Pareto边界中，并且是最优的，因为边界中的任何解都不能在不损害其至少一个目标的情况下得到改进。因此，进化算法将种群进化为产生更靠近帕累托边界的个体，然后线性搜索返回仅使三个目标的平均值（或其他组合，如我们在下一节中看到的）最大化的个体。在这种策略下，我们遵循著名的强度Pareto进化算法方法[36]，该方法被证明是非常有效的，并且与现有方法[11，13，32]相比，它为许多有意思的问题提供了更多样的结果。强度帕累托方法将个体分离出来，这些个体通过进化出可能不受群体中其他个体支配的个体，在最大化竞争目标之间达成妥协。

It is worth noticing that our approach does not depend on which recommendation algorithms are being aggregated, nor does it depend on the data domain. This makes adding or removing algorithms trivial, and allows the data to determine how each algorithm contributes to each of the objectives - an algorithm may be the most accurate when ratings are available, but not so accurate when only implicit feedback is used.
The Pareto-Optimal search is computationally expensive. However, it can be performed in an offline manner, and with low frequency. After the Pareto-Optimal weights are discovered, there is no need to perform the search repeatedly, unless a recommendation algorithm is added or removed, or a lot of new feedback data enters the system. Therefore, using this approach would not hinder the system’s online performance.

值得注意的是，我们的方法不依赖于聚合哪些推荐算法，也不依赖于数据域。这使得添加或删除算法变得很简单，并能确定每个算法对每个目标的贡献-当评级可用时，一个算法可能是最精确的，但当仅使用隐式反馈时，则不是那么精确。

帕累托最优搜索在计算上是昂贵的。但是，它可以以离线方式和低频率执行。在发现Pareto最优权值后，无需重复搜索，除非加入或删除推荐算法，或大量新的反馈数据进入系统。因此，使用这种方法不会妨碍系统的在线性能。

 

3.3 Adjusting the System Priority 调整系统优先级

It is well recognized that the role that a recommender system plays may vary depending on the target user. For instance, according to [19], the suggestions performed by a recommender system may fail to appear trustworthy to a new user because it does not recommend items the user is sure to enjoy but probably already knows about. Based on this, a recommender system might prioritize accuracy instead of novelty or diversity for new users, while prioritizing novelty for users that have already used the system for a while. This is made possible by our hybridization approach, by searching which individual in the Pareto frontier better solves the user’s current needs.
The choice of which individual in the Pareto frontier is accomplished by performing a linear search on all of the individuals, in order to find which one maximizes a simple weighted mean on each of the three objectives in the objective vector, where the weights in the weighted mean represent the priority given to each objective. It is worth noting that fitness values are always calculated using the cross-validation set. Therefore, considering a 3-dimensional priority vector Q, which represents the importance of each objective j, the individual in the Pareto frontier P is chosen as:

众所周知，推荐系统扮演的角色可能因目标用户而异。例如，根据[19]，推荐系统的推荐可能对新用户不太准确，因为它无法推荐用户肯定会喜欢但可能已经知道的物品。基于此，对新用户来说，推荐系统可能会优先考虑准确性，而不是新颖性或多样性；而对已经使用过系统的用户来说，优先考虑新颖性。这是通过我们的混合方法实现的，通过搜索帕累托前沿的哪个个体更好地解决了用户当前的需求。

帕累托前沿中的个体选择是通过对所有个体进行线性搜索来完成的，以便找出哪个个体最大化了目标向量中三个目标的简单加权均值，其中加权平均值中的权重表示赋予每个目标的优先级。值得注意的是，适应度值是使用交叉验证集计算的。因此，考虑到代表每个目标j的重要性的三维优先向量Q，帕累托前沿P中的个体被选择为：

 

4. EVALUATION METHODOLOGY 评估方法

The testing methodology we adopted in this paper is similar to the one described in [12], which is appropriate for the top-N recommendation task. For each dataset, ratings are split into two subsets: the training set M and the test set T. The training set M can (if necessary) be split into two subsets: the cross-validation training set C and the cross-validation test set V, which is used in order to tune parameters or adjust models. The test set T and the cross-validation test set V only contain items that are considered relevant to the users in the set. For explicit feedback (i.e., MovieLens), this means that the sets T and V only contain 5-star ratings.

本文采用的测试方法与文献[12]中描述的方法相似，适合于top-N推荐任务。对于每个数据集，评分被分成两个子集：训练集M和测试集T。训练集M可以（如有必要）分为两个子集：交叉验证训练集C和交叉验证测试集V，用于调整参数或调整模型。测试集T和交叉验证测试集V只包含被认为与集合中的用户相关的项。对于显式反馈（比如，MovieLens），这意味着集合T和V只包含5星评级。

In the case of implicit feedback (i.e., Last.fm), we normalized the observed item access frequencies of each user to a common rating scale [0,5], as used in [33]. Namely, , where is the number of times u has accessed i and is the cumulative distribution function of  over the set of items accessed by the user u, denoted as u. In this case, the test set and the cross validation test set only contain ratings such that r(u, i) >= 4, since the number of 5 star ratings is very small using this mapping of implicit feedback into ratings. It is worth noting that all the sets have a corresponding implicit feedback set, used by the recommendation algorithms that can deal with implicit feedback.

在隐式反馈（比如，Last.fm）的情况下，我们将每个用户对看过的物品的访问频率标准化为一个通用的评分标准[0,5]，如[33]中所用。即，其中，是u访问i的次数，是在用户u访问的物品集合上的累积分布函数，表示为u。测试集和交叉验证测试集只包含r(u, i) >= 4的评分，因为隐式反馈到评分的映射，五星评分的数量非常小。值得注意的是，所有的集合都有一个对应的隐式反馈集合，用于处理隐式反馈的推荐算法。

The detailed procedure to create M and T is the same used in [12], in order to maintain compatibility with their results. Namely, for each dataset we randomly sub-sampled 1.4% of the ratings from the dataset in order to create a probe set. The training set M contains the remaining ratings, while the test set T contains all the 5-star ratings in the probe set (in the case of explicit feedback) or 4+ star ratings (in the case of implicit feedback mapped into explicit feedback). We further divided the training set in the same fashion, in order to create the cross-validation training and test sets C and V. The ratings in the probe sets were not used for training.
In order to evaluate the algorithms, we first train the models using M. Then, for each item in T that is relevant to user u:
• We randomly select 1,000 additional items unrated by user u. The assumption is that most of them will not be interesting to u.
• The algorithm in question forms a ranked list by ordering all of the 1,001 items. The most accurate result corresponds to the case where the test item i is in the first position.

创建M和T的详细过程与[12]中使用的相同，以保持其结果的兼容性。也就是说，对于每个数据集，我们从数据集中随机抽取1.4%的评分，以创建一个探测集。训练集M包含剩余的评分，而测试集T包含探测集中的所有5-star评分（在显式反馈的情况下）或4+star评分（在隐式反馈映射为显式反馈的情况下）。我们以同样的方式进一步划分训练集，以创建交叉验证训练集和测试集C和V。探针集中的评分不用于训练。

为了评估算法，我们首先使用M训练模型，然后，对于T中与用户u相关的每个项：

•我们随机选择1000个未经用户u评分的附加项目。假设是u对其中的大多数物品不感兴趣。

•所讨论的算法对所有1001个物品排序形成一个排序列表。最准确的结果对应于试验物品i处于第一位置的情况。

 

Since the task is top-N recommendation, we form a top-N list by picking the N items out of the 1,001 that have the highest rank. If the test item i is among the top-N items, we have a hit. Otherwise, we have a miss. Recall and precision are calculated as follows:

                (4)

               (5)

In order to measure the novelty of the recommendations, we used a popularity-based item novelty model proposed in [33], so that the probability of an item i being seen is estimated as:

where U denotes the set of users. Since the testing methodology supposes that most of the 1,000 additional unrated items are not relevant, we used the metrics in the framework proposed in [33] without relevance awareness. The novelty of a top-N recommendation list from R presented to user u is therefore given by:

            (7)

where rd(k) is a rank discount giver by [33] and C is a normalizing constant given by . Therefore, 
this metric is rank-sensitive (i.e. the novelty of the top-rated items counts more than the novelty of other items). As is the case with precision and recall, we average the EPC@N value of the top-N recommendation lists over the test set.
We used a distance based model in order to measure the diversity of the recommendation lists. Once again, we used the metrics from [33] without relevance-awareness. The recommendation diversity, therefore, is given by:

where rd (l|k) = rd (max (1, l−k)) reflects a relative rank discount between l and k, and is the cosine similarity between two items, given by:

such that  denotes the users that liked item i, and  denotes the users that liked item j.

 

由于是top-N推荐，我们从1001个物品中选出排名最高的N个物品，从而形成top-N列表。如果测试物品i在前N个物品中，则为hit。否则，为miss。召回率和精确度计算如下：

                (4)

               (5)

 

为了衡量这些推荐的新颖性，我们使用了[33]中提出的基于流行度的物品新颖性模型，看的物品i的概率为：

其中U表示用户集。由于测试方法假设1000个额外的未评分物品中的大多数都不相关，我们使用了[33]中提出的框架中的度量。因此，向用户u呈现的R的top-N推荐列表的新颖性为：

            (7)

其中rd(k)为排序衰减因子，[33]，C是归一化常量。因此，这个指标是排序敏感的（即，排序最高的物品的新颖性远远高于其他物品）。与精确性和召回率一样，我们在测试集上对前N个推荐列表的EPC@N值做了平均。

我们使用基于距离的模型来衡量推荐列表的多样性。我们使用了[33]中的度量标准。推荐的多样性如下：

where rd (l|k) = rd (max (1, l−k))反映了l和k之间的相对排序衰减， 是两个物品的余弦相似性，由下式给出：

 表示喜欢物品i的用户， 表示喜欢物品j的用户。

5. EXPERIMENTAL EVALUATION 实验评估

We apply the methodology presented in Section 4 to two different scenarios, in order to evaluate our hybrid approach: movie and music recommendation. For movie recommendation, we used the MovieLens dataset [27]. This dataset contains 1,000,209 ratings from 6,040 users on 3,883 movies. For music recommendation, we used an implicit preference dataset from [9], which consists of 19,150,868 user accesses to music tracks on the website Last.fm. This dataset involves 176,948 artists and 992 users, and we considered the task of recommending artists to users. Mapping the implicit feedback into user-artist ratings yielded a total of 889,558 ratings, which were used by the algorithms that cannot deal with implicit feedback, and to separate the dataset into the training and test sets M and T .

我们将第4节中介绍的方法应用于两个不同的场景，以评估我们的混合方法：电影和音乐推荐。对于电影推荐，我们使用MovieLens数据集[27]。这个数据集包含来自3883部电影6040个用户的1000209个评分。对于音乐推荐，我们使用了来自[9]的隐式偏好数据集，该数据集由19150868个用户访问网站Last.fm1上的音乐曲目组成。这个数据集涉及176948个艺术家和992个用户，我们考虑的是向用户推荐艺术家的任务。将隐式反馈映射到用户-艺术家评分中，得到了889558个评分，把这些评分用到无法处理隐式反馈的算法中，并将数据集分离为训练集和测试集M和T。

5.1 Recommendation Algorithms 推荐算法

We selected eight recommendation algorithms to provide the base for our hybrids. To represent latent factor models, we selected PureSVD with 50 and 150 factors (PureSVD50 and PureSVD150), described in [12]. These were the only algorithms we used that are based on explicit feedback. To compute the scores for the items in the Last.fm dataset, we used the mappings of implicit feedback into ratings explained in Section 5.3.
As for recommendation algorithms that use implicit feedback, we used algorithms available in the MyMediaLite package [16]. We used WeightedItemKNN (WIKNN) and WeightedUserKNN (WUKNN) as representative of neighbourhood models based on collaborative data [14] (we only used WeightedItemKNN on the MovieLens dataset, as MyMediaLite’s implementation cannot yet handle datasets where the number of items is very large, which is the case in the Last.fm dataset). As a baseline, and to allow for comparison with [12], we used MyMediaLite’s MostPopular implementation, which is the same as TopPop in [12]. We also used WRMF − a weighted matrix factorization method based on [21, 29], which is very effective for data with implicit feedback. In order to represent content-based algorithms, we used ItemAttributeKNN(IAKNN), a K-nearest neighbor item-based collaborative filtering using cosine-similarity over the movie genres for MovieLens (we could not use this method in the Last.fm dataset, because it does not contain content data). Finally, we used UserAttributeKNN(UAKNN), a K-nearest neighbor user-based collaborative filtering using cosine-similarity over the user attributes, such as sex, age, etc. (which both datasets provide).

在混合推荐中，我们选择了8种推荐算法。为了表示潜在因素模型，我们选择了具有50和150个因素（PureSVD50和PureSVD150）的PureSVD，如[12]所述。这些是我们使用的唯一基于显式反馈的算法。为了计算Last.fm数据集中各项的得分，我们使用了第5.3节中解释的隐式反馈到评分的映射。

对于使用隐式反馈的推荐算法，我们使用MyMediaLite包中提供的算法[16]。我们使用WeightedItemKNN（WIKNN）和WeightedUserKNN（WUKNN）两个基于协作数据[14]的邻域模型（我们只在MovieLens数据集上使用WeightedItemKNN，因为MyMediaLite的实现还不能处理物品数非常大的数据集，Last.fm数据集也是这样）。作为基线，为了与[12]进行比较，我们使用MyMediaLite的MostPopular实现，它与[12]中的TopPop相同。我们还使用了基于[21，29]的加权矩阵因式分解方法WRMF，它对隐式反馈的数据非常有效。为了表示基于内容的算法，我们使用itematributeknn（IAKNN），这是一种K近邻基于item的协同过滤，在MovieLens的电影类型上使用余弦相似性（在Last.fm数据集中不能使用此方法，因为它不包含内容数据）。最后，我们使用了UserAttributeKNN（UAKNN），这是一种K近邻基于user的协同过滤，对用户属性（如性别、年龄等）使用余弦相似度。

5.2 Hybrid Approaches 混合方法

As a baseline, we used a voting-based hybrid based on Borda-Count (BC) which is similar to [30], where each constituent algorithm gives n points to each item i such that , where |R| is the size of the recommendation list and is the position of i in R. We also used STREAM as baseline, a stacking-based approach with additional meta-features [3]. We used the same additional meta-features as [3], namely, the number of items that a certain user has rated and the number of users that has rated a certain item (denoted as and in [3]). We tried the learning algorithms proposed in [3], and Linear Regression yielded the best results, so the results presented for STREAM are generated using Linear Regression as the meta-learning algorithm. Our last baseline is the weighted hybrid we proposed in Section 3.1, using equal weights for each constituent algorithm. We called this baseline Equal Weights (EW).
As for our genetic approach, we combined all of the the recommendation algorithms cited in the last subsection. We used an open-source implementation of SPEA2 [36, 37] from DEAP [31]. We used a two points crossover operator [20], and a uniform random mutation operator with probability 0.05. SPEA-2 was configured with the following parameters:

作为基线，我们使用基于Borda-Count (BC)的基于投票的混合算法，类似于[30]，其中每个组成算法给每个物品i赋n个点，使得，其中|R|是推荐列表的大小，是i在R中的位置。我们还使用STREAM作为基线，一种附加元特征的基于叠加(stacking-based)的方法[3]。我们使用了与[3]相同的附加元特性，即，某个用户评分的物品数和对某个项目进行了评分的用户数（在[3]中表示为和）。我们尝试了文献[3]中提出的学习算法，线性回归得到了最好的结果，因此STREAM的结果是使用线性回归作为元学习算法生成的。我们的最后一个基线是我们在第3.1节中提出的加权混合，对每个组成算法使用相等的权重。我们称之为基线等权重（EW）。

至于我们的遗传方法，我们结合了上一小节中引用的所有推荐算法。我们使用了来自DEAP[31]的SPEA2[36，37]的开源实现，我们使用了两点交叉算子[20]和概率为0.05的均匀随机变异算子。SPEA-2的参数配置如下：

 

5.3 Results and Discussion 结果和讨论

The results achieved by each of the constituent recommendation algorithms can be seen in Tables 1 and 2. We show the accuracy results (recall and precision) over different values of N. Since both EPC(novelty) and EILD(diversity) are rank-sensitive metrics, we only presented their values for N = 20. There is a clear compromise between accuracy, novelty and diversity of these algorithms. For the MovieLens dataset (Table 1), the constituent algorithm that provides the most accurate recommendations is PureSVD50. The constituent algorithm that provides the most novel recommendation with an acceptable degree of accuracy is PureSVD150, but its accuracy is much worse than the accuracy obtained by PureSVD50, and its diversity is much worse than the other algorithms. TopPop provided the most diverse recommendations, although it performs significantly worse in accuracy and novelty. It is worth noting that ItemAttributeKNN is based only on genres, which explains its poor accuracy results.

各组成推荐算法的结果见表1和表2。我们给出了N为不同值时的准确性结果（召回率、准确率）。由于EPC（新颖性）和EILD（多样性）都是排序敏感的度量，我们只给出了N=20的新颖性和多样性结果。这些算法的准确性、新颖性和多样性之间存在着明显的折衷。对于MovieLens数据集（表1），提供最准确推荐的组成算法是PureSVD50。PureSVD150算法是新颖度最好的推荐算法，其推荐精度可以接受，但其推荐精度远低于PureSVD50算法，其多样性远低于其他算法。TopPop提供了最多样化的推荐，但是它在准确性和新颖性方面的表现要差得多。值得注意的是，ItemAttributeKNN只基于类别进行推荐，这就解释了其准确性差的原因。

On the Last.fm dataset, the constituent algorithm that provides the most accurate recommendations is WRMF. This is expected, as Last.fm is originally an implicit feedback dataset, to which WRMF is more suitable. Once again, PureSVD150 proved its capacity to suggest novel items, being the algorithm with the most novel recommendations. WeightedUserKNN proved to be the algorithm that provided the most diverse recommendations, while maintaining a reasonable accuracy degree. In this dataset the compromise between the three objectives is once again illustrated by the fact that there is no algorithm that dominates the others in every objective.

在Last.fm数据集上，提供最准确推荐的组成算法是WRMF。这是符合预期的，因为Last.fm最初是一个隐式反馈数据集，WRMF更适合它。PureSVD150再一次证明了它提出新颖物品的能力，它是新颖性最好的推荐算法。WeightedUserKNN在保持合理精度的前提下，提供了最多样化的推荐。在这个数据集中，这三个目标之间的折衷再一次被这样一个事实所说明：没有一个算法能在所有目标上支配其他算法。

Regarding the performance of the baselines in the MovieLens dataset, STREAM performs worse then PureSVD50 on accuracy, maintaining the same level of novelty and performing better in terms of diversity. Borda Count performed poorly on accuracy and reasonably well in terms of novelty and diversity. Equal Weights performed poorly on accuracy and novelty and well on diversity. On the Last.fm dataset, STREAM performed slightly worse than WRMF in accuracy, while maintaining the same level of diversity and improving slightly on novelty. Once again, Borda Count performed poorly on accuracy and reasonably well on novelty and diversity. Finally, Equal Weights performed poorly on accuracy and novelty, while performing well on diversity.

关于MovieLens数据集中基线的性能，STREAM在精度上比PureSVD50差，新颖性表现相同，在多样性方面表现更好。Borda Count在准确性方面表现不佳，在新颖性和多样性方面表现相当不错。Equal Weights在准确性、新颖性方面表现不佳，在多样性上表现很好。在Last.fm数据集上，STREAM的准确度略低于WRMF，多样性表现相当，在新颖性上略有提高。同样，Borda Count在准确性上表现不佳，在新颖性和多样性方面表现良好。最后，Equal Weights在准确性和新颖性方面表现不佳，而在多样性方面表现良好。

Now, with our evolutionary approach, we could reach any of the individuals in Figure 1, which represent the accuracy (in this case, Recall@10) and novelty (EPC@20) of the recommendations in x and y axes, and diversity (EILD@20) with a color scale. These graphics show the results in the test set for the individuals that represented the Pareto frontier in the cross-validation. It is clear that there is a compromise between the three objectives: the individuals with the most novel recommendations provide less accurate and diverse lists, and so on. This compromise can be adjusted dynamically with little extra cost, since the cost of reaching these individuals is as low as a linear search (for the individual that maximizes a weighted mean, as described on Section 3.2) over the Pareto frontier individuals’ scores on the cross validation set. The Pareto frontier consists of 1,418 individuals in the MovieLens dataset and of 1,995 individuals in the Last.fm dataset, so a linear search can be done very quickly. We chose to demonstrate a few of these individuals in Tables 1 and 2. First, Pareto-Optimal-mean (PO-mean) represents the individual that optimizes the mean of the three normalized objectives, assuming each of them are equally important. This would be an option if personalization was not desired, or if the designers of the recommender systems did not know which combination of the three objectives would result in higher user satisfaction. However, in a more realistic situation, the recommender system would most likely want to select different individuals for different users. We selected as examples the following individuals, which were found by the process explained in Section 3.2 with the represented associated weighted vectors:

• PO-acc: [Accuracy:0.85, Novelty:0.1, Diversity:0.05]
• PO-acc2: [Accuracy:0.7, Novelty:0.3, Diversity:0]
• PO-nov: [Accuracy:0.15, Novelty:0.85, Diversity:0]
• PO-div: [Accuracy:0.15, Novelty:0.15, Diversity:0.7]

现在，通过我们的进化方法，我们可以达到到图1中的任何个体，这些个体代表了x和y轴上推荐的准确性（在本例中，Recall@10）和新颖性（EPC@20），以及用各种颜色表示的多样性（EILD@20）。这些图形显示了交叉验证中代表Pareto前沿的个体的测试集结果。很明显，这三个目标之间存在一种折衷：推荐最新颖的个体提供的列表不够准确和多样，等等。这种折衷可以动态地进行调整，而不需要太多额外的成本，因为达到这些个体的成本比较低，在交叉验证集中的帕累托前沿个体的得分上进行线性搜索（对于加权平均值最大的个体，如第3.2节所述）即可。帕累托边界由MovieLens数据集中的1418个个体和Last.fm数据集中的1995个个体组成，因此可以非常快速地进行线性搜索。我们在表1和表2中显示了其中一些个体。首先，帕累托最优均值（PO-mean）表示优化三个标准化目标均值的个体，假设每个目标都同等重要。如果不需要个性化，或者如果推荐系统的设计者不知道这三个目标的哪一个组合将导致更高的用户满意度，可以这样来做。然而，在更现实的情况下，推荐系统很可能希望为不同的用户选择不同的个体。我们选择了以下个体作为例子，通过第3.2节中所述的过程和所代表的相关加权向量发现这些个体：

• PO-acc: [Accuracy:0.85, Novelty:0.1, Diversity:0.05]
• PO-acc2: [Accuracy:0.7, Novelty:0.3, Diversity:0]
• PO-nov: [Accuracy:0.15, Novelty:0.85, Diversity:0]
• PO-div: [Accuracy:0.15, Novelty:0.15, Diversity:0.7]

We compared PO-acc and PO-acc2 with PureSVD50, which is the standalone algorithm with the most accurate recommendations. Both perform as well as PureSVD50 on accuracy, but PO-acc performs much better on diversity (and equally well on novelty), and PO-acc2 performs better on novelty while maintaining the diversity level. We compared PO-nov with Pure-SVD150, which presented the most novel recommendations to the users, with reasonable accuracy. PO-nov performs slightly better on novelty than PureSVD150, but performs much better in terms of accuracy, and slightly on diversity. Finally, we compared PO-div with MostPopular, the algorithm with the most diverse recommendations. PO-div loses very slightly on diversity, while improving on accuracy and novelty. We were able, therefore, to find individuals in the Pareto frontier that performed close or better than the best algorithms in each individual objective, but better on the other objectives. Once again, we could have chosen to compromise more accuracy and diversity if we desired more novelty, as is shown by Figure 1 (left).
As for the Last.fm dataset, we selected the following individuals: 
• PO-acc: [Accuracy:0.7, Novelty:0.3, Diversity:0]
• PO-nov: [Accuracy:0.15, Novelty:0.85, Diversity:0]
• PO-div: [Accuracy:0.45, Novelty:0.05, Diversity:0.5]

我们将PO-acc和PO-acc2与PureSVD50进行了比较，PureSVD50是具有最精确推荐的独立算法。两者在准确性上的表现都和PureSVD50一样好，但是PO-acc在多样性上表现得更好（在新颖性上也同样好），PO-acc2在保持多样性水平的同时在新颖性上表现得更好。我们将PO-nov与Pure-SVD150进行了比较，后者给用户的推荐最新颖，并且具有合理的准确性。与PureSVD150相比，PO-nov在新颖性方面表现稍好，但在准确性方面表现更佳，在多样性方面表现稍好。最后，我们比较了PO-div和MostPopular算法，该算法的推荐多样性最好。PO-div在多样性方面稍差，在准确性和新颖性方面有所提高。因此，我们能够在帕累托前沿找到在每个目标上表现接近或优于最佳算法的个体，但在其他目标上表现更好。如果我们想要更多的新颖性，我们可以选择牺牲更多的准确性和多样性，如图1（左）所示。

对于Last.fm数据集，我们选择了以下个体：

• PO-acc: [Accuracy:0.7, Novelty:0.3, Diversity:0]
• PO-nov: [Accuracy:0.15, Novelty:0.85, Diversity:0]
• PO-div: [Accuracy:0.45, Novelty:0.05, Diversity:0.5]

For the Last.fm dataset, we compared PO-acc with WRMF, which is the most accurate standalone algorithm on this dataset. PO-acc is much more accurate than WRMF, while also improving on novelty and maintaining the diversity level. The individual PO-nov was compared with PureSVD150, and it performed equally well on accuracy, while delivering a much higher novelty, and only a slightly worse diversity. PO-div was compared against WeightedUserKNN, and it faired equally well on diversity and novelty, while slightly improving on accuracy. It is worth noticing that the individual represented by PO-div is the same individual that maximizes the mean with equal weight (PO-mean). Once again, we were able to find interesting individuals in the Pareto frontier, but we could have reached any of the individuals in Figure 1 (right) by tweaking the weight value for each objective.

对于Last.fm数据集，我们比较了PO-acc和WRMF，后者是该数据集上最精确的独立算法。PO-acc比WRMF精确得多，在新颖性方面有改进，多样性相当。我们将PO-nov与PureSVD150进行了比较，它在准确性方面同样表现良好，同时提供了更高的新颖性，多样性只稍微差一点。将PO-div与WeightedUserKNN进行了比较，它在多样性和新颖性方面表现得同样出色，在准确性方面略有提高。值得注意的是，PO-div所代表的个体是用等权最大化平均值（PO-mean）的同一个体。我们在帕累托边界找到了有趣的个体，但是我们可以通过调整每个目标的权重值来达到图1（右）中的任何个体。

6. CONCLUSIONS

In this paper, we propose a hybridization technique for combining different recommendation algorithms, following the Strength Pareto approach. We show that different recommendation algorithms do not perform uniformly well when evaluated in accuracy, novelty and diversity, but our technique allows for the dynamic adjustment of the compromise between these three aspects of user satisfaction. This can be very useful in different scenarios, one example being the personalization of recommendations according to the users. According to [25], “New users have different needs from experienced users in a recommender. New users may benefit from an algorithm which generates highly ratable items, as they need to establish trust and rapport with a recommender before taking advantage of the recommendations it offers.” Therefore, our approach could be used to provide new users with the most accurate recommendations as possible, even if the recommendations are not novel at all - so the users would have items to rate, and build trust in the system. The costly part of our technique (the evolutionary algorithm) is performed offline, and the online cost of choosing an individual in the pareto frontier and weighting the results for different algorithms is very small, since the pareto frontier is comprised of few individuals.
We performed highly reproducible experiments on public datasets of implicit and explicit feedback, using open-source implementations. In our experiments, we demonstrated our technique’s ability to balance each of the objectives according to the desired compromise, and we showed some examples of reached solutions that are competitive with the best algorithms according to each objective and almost always better on the other objectives.

在本文中，遵循强度帕累托方法，我们提出了一种混合技术，来组合不同的推荐算法。我们发现不同的推荐算法在准确性、新颖性和多样性方面的表现并不一致，但是我们的技术允许动态调整用户满意度这三个方面之间的折衷。这在不同的场景中非常有用，例如根据用户个性化推荐。根据[25]，“新用户和老用户对推荐有不同的需求。新用户可能更喜欢高点击率的物品，因为他们需要在使用推荐系统之前与推荐系统建立信任和关系。”因此，我们的方法可以用于为新用户提供尽可能准确的推荐，即使推荐一点都不新颖-这样用户就可以对物品进行评分，并在系统中建立信任。我们技术中耗费资源的部分（进化算法）是离线执行的，而在帕累托前沿选择个体并为不同算法的结果加权的在线成本非常小，因为帕累托前沿由很少的个体组成。

我们使用开放源代码实现，对隐式和显式反馈的公共数据集进行了高度可重复的实验。我们的技术可以根据期望的折衷来平衡每个目标，并且给出了一些解决方案的例子，这些解决方案在单目标上与最佳算法性能相当，在其他目标上，表现更好。