冈萨雷斯数字图像处理-数字图像基础（Matlab）-图像的频域滤波

前面的章节我们介绍了图像的灰度变换以及空间域滤波，本章我们介绍图像的频域滤波。

什么是频率？

频率我们可以直观的理解为空间或者时间的变化率。

对于图像来说，傅里叶变换中的频率与图像中的亮度变化直接联系。傅里叶变换的原点表示直流分量或者说是图像的平均灰度。例如，房间中的墙和地板，没有云朵的蔚蓝的天空等等，这些场景中图像变化缓慢，或者几乎不变，这里就对应着傅里叶变换的原点分量或者低频分量。而对于各种纹理、物体的边缘等灰度急剧变化的地方而言，则对应于傅里叶变换的高频分量。

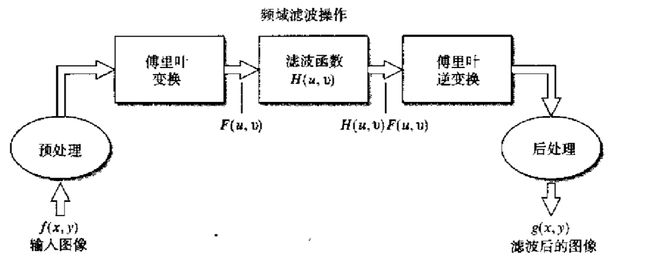
频率域滤波流程

图像的频域滤波可以理解为：将图像进行傅里叶变换，使空间域变换到频率域，然后在频率域进行相关滤波操作，最后通过傅里叶逆变换得到滤波后的图像。整个流程如图所示。

傅里叶变换操作

下面我们简单以一张图片为例说明傅里叶变换。由图像直观来看，图像基本为单色调，除去白色矩形边框，几乎没有颜色变化，因此该图像的傅里叶变换几乎主要集中在原点处。

我们首先对该图直接进行FFT

clear
clc
data = imread('Fig0424(a)(rectangle).jpg');
data = rgb2gray(data);
figure(1)
imshow(data)
title('原图像')
F = fft2(data);
S = im2uint8(mat2gray(abs(F)));
figure(2)
imshow(S)
title('傅里叶变换-在4个角显示亮点的谱')

我们可以得到下图，注意该图的4个角显示有亮点，其值就是为傅里叶变换的原点。

                      

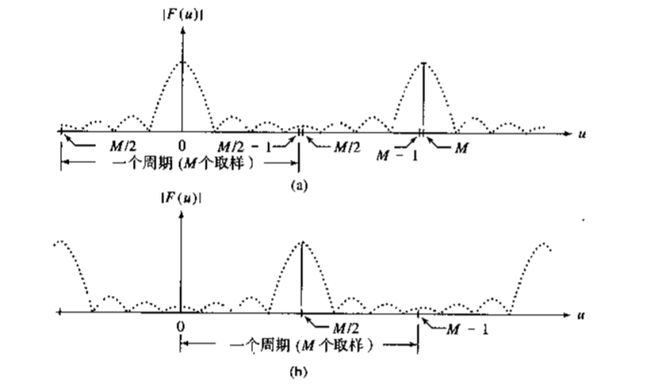
这是因为在图像的傅里叶变换中，傅里叶变换为周期函数和对称函数，如下图所示，在原点以左的半个周期中，变换的幅度值从M/2到M-1重复。因为一维FFT仅在M个点上实现，所以在该区域计算机一维变换将产生两个紧邻的半周期。而我们希望在区间[0,M-1]内得到一个完整且正确排序的周期。而我们可以采用在计算前让f(x)乘以(-1)^x来得到。这样做可以将变换的原点移动到点u=M/2处。

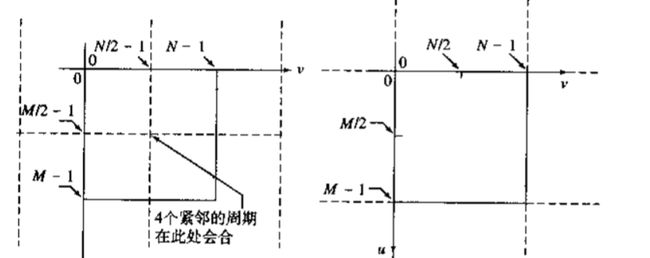
同理，对于二维图像也是这样。如图所示。二维图像的傅里叶变换也是周期性和对称性的，因此，其原点的值位于图像的四个角，若想将其移动到中心，需要将图像在傅里叶变换之前乘以(-1)^(x+y)。

下面我们利用Matlab对其进行处理：

Fc = fftshift(S);
figure(3)
imshow(Fc)
title('傅里叶变换-中心化后的谱')

这里的fftshift函数就是将其傅里叶变换移动到中心。我们可以得到下图：

我们可以看到傅里叶变换的能量确实集中在低频区域。由于图像的频域分布较广，无法全部显示出来，牺牲了部分细节，这里我们可以通过对数变换得到更多的细节。

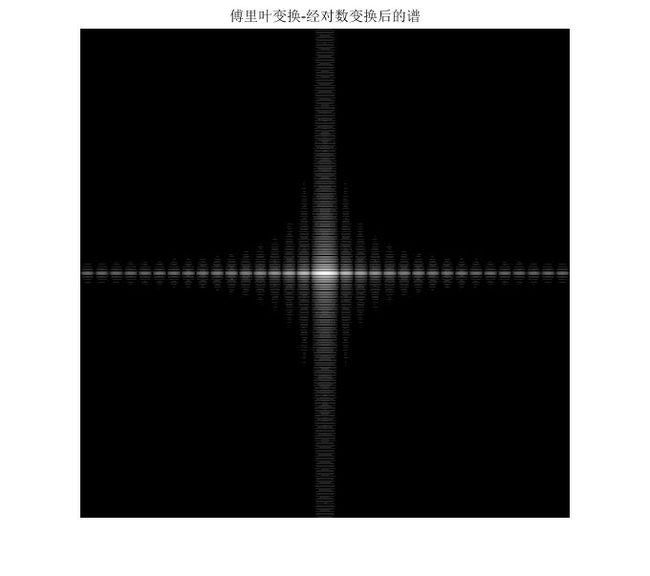
newFc = im2uint8(mat2gray(log(1+double(Fc))));
figure(4)
imshow(newFc)
title('傅里叶变换-经对数变换后的谱')

图像的傅里叶变换也有一些很好的性质，如图所示，我们将图片旋转了45°，其频谱图也相应的旋转了45°。

图像的傅里叶变换谱的分量决定了正弦波的幅度，较大的分量意味着在图像中该频率的正弦波比较图出，其模值决定了图像的灰度，相位则携带着图像中的物体定位信息。

如图所示为一名女性的图片：

我们可以得到该图片傅里叶变换的相角：

Fig24= imread('Fig0424(a)(rectangle).jpg');
Fig24 = rgb2gray(Fig24);
Fig27= imread('Fig0427(a)(woman).jpg');
Fig27 = rgb2gray(Fig27);
figure(1)
subplot(1,2,1)
imshow(Fig24)
title('rectangle')
subplot(1,2,2)
imshow(Fig27)
title('woman')
suptitle('原图像')
%%傅里叶变换
F24 = fft2(Fig24);
S24 = im2uint8(mat2gray(abs(F24)));

F27 = fft2(Fig27);
S27 = im2uint8(mat2gray(abs(F27)));

Fc27 = fftshift(F27);
ang27=angle(F27);
figure(2)
fig2 = im2uint8(mat2gray(ang27));
imshow(fig2)
title('women 傅里叶变换的相角')

这里，我们令傅里叶变换的模值为1，只保留傅里叶变换的相角，然后我们对其进行傅里叶逆变换“

figure(3)
fig3 = im2uint8(mat2gray(ifft2(double(F27./(abs(F27))))));
imshow(fig3)
title('women 仅使用相角重建的妇女图像')

我们可以看到，只用傅里叶变换的相位信息就可以得到原图像的关键形状信息，只是相应的灰度信息（由谱携带）丢失了。

然后我们仅使用谱进行傅里叶逆变换，即将相角设置为0：

figure(4)
fig4 = im2uint8(mat2gray(ifft2(double(abs(F27)))));
imshow(fig4)
title('women 仅使用谱重建的妇女图像')

我们可以看到它仅包含灰度信息，图像中没有形状信息。（如果图像中不够明显，可以通过对数变换更为直观的观测）

接下来我们将上述相位和矩形图的傅里叶谱结合重建，由于两张图片大小不同，这里我们每隔1个点取一个值。

figure(5)
F24_2 = F24(1:2:1024,1:2:1024);
fig5 = im2uint8(mat2gray(ifft2(double(abs(F24_2).*F27./abs(F27)))));
imshow(fig5)
title('women 使用矩形的相角和妇女图像的谱重建的图像')

我们可以看出，确定一幅图像的特性内容时，相位起到支配作用。

频域滤波

在前面介绍了图像的傅里叶变换和频域滤波的流程后，我们简要介绍几个图像的频域滤波实例。

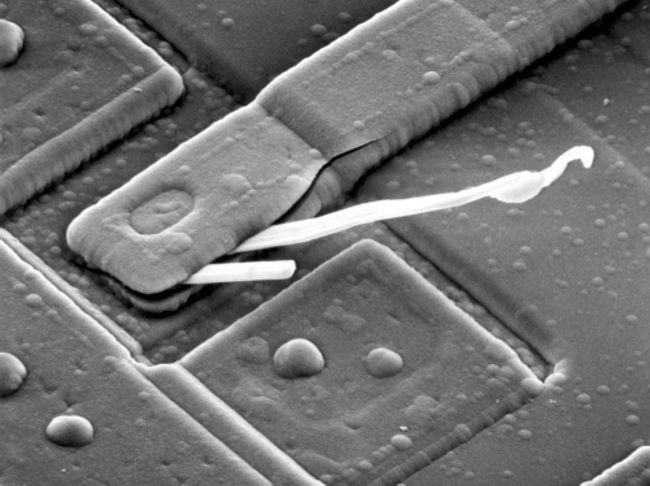
下面是一张由于热感应故障受损的灰色电路板的图片。

我们首先获得它的傅里叶变换谱。为了便于观测，我们进行了两次取对数。

clear
clc
data = imread('Fig0429(a)(blown_ic).jpg');
data = rgb2gray(data);
figure(1)
imshow(data)
title('原图像')

[m,n] = size(data);
F = fft2(data)/(m*n);
Fc = fftshift(F);
figure(2)
fig2 = im2uint8(mat2gray(log(1+double(abs(Fc)))));
fig2 = im2uint8(mat2gray(log(1+double(fig2))));
imshow(fig2)
title('傅里叶变换谱')

可以看到，该电路板的频谱主要集中在低频部分，图像中还有两个沿±45°方向的突出分量，这些分量对应于原图像中电路板的边缘以及两个由于热感应故障导致的白色氧化突起物。

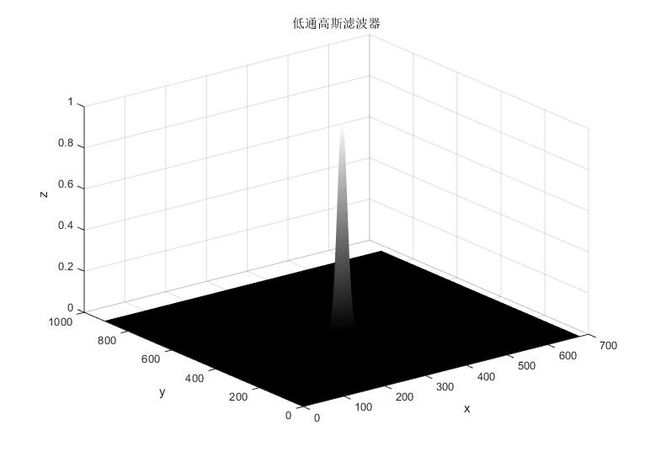
我们首先生成一个低通高斯滤波器：

sig = 10;
H = fspecial('gaussian',[m,n],sig);
H = mat2gray(H);%将其映射到[0,1]中
x=1:m;
y=1:n;
[X,Y] = meshgrid(x,y);
figure(3)
mesh(X',Y',H)
title('低通高斯滤波器')
xlabel('x')
ylabel('y')
zlabel('z')

我们知道对于傅里叶变换，时域（空间域）的卷积相当于频率域的乘积，因此我们通过低通滤波器得到滤波后的图像：

G = H.*Fc;
g1 = ifft2(G);
g1 = im2uint8(mat2gray(abs(g1)));
figure(4)
imshow(g1)
title('滤波后的图像')

我们可以看到通过低通滤波器后，由于高频分量衰减，因此对于一些边缘细节将会失去，我们可以直观的理解为低通滤波器模糊了一张图像。

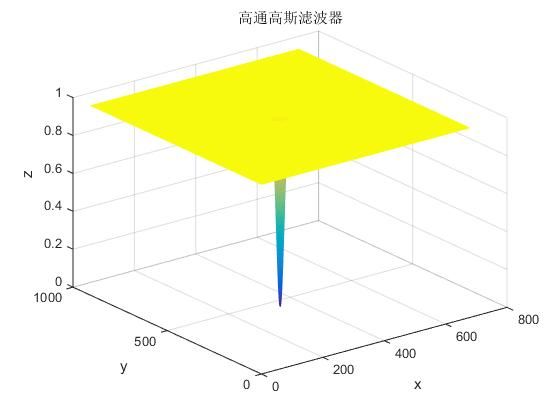
下面我们通过高通高斯滤波器，通过1-H得到：

figure(5)
H2 = mat2gray(1-H);  %将其映射到[0,1]中
[a,b] = find(H2 ==min(min(H2)));
mesh(X',Y',H2)
title('高通高斯滤波器')
xlabel('x')
ylabel('y')
zlabel('z')

同样我们可以得到滤波后的图像：

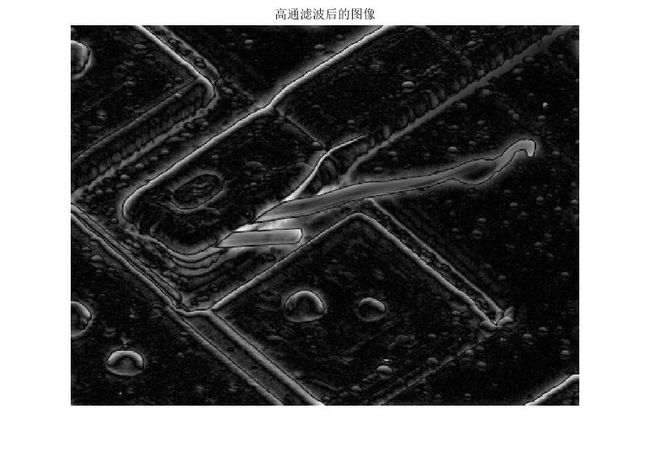
G2 = H2.*Fc;
g2 = ifft2(G2);
g2 = im2uint8(mat2gray(abs(g2)));
figure(6)
imshow(g2)
title('高通滤波后的图像')

我们可以看到通过高通滤波器，直观上将增强了尖锐的细节，但是由于直流量的丢失，图像的灰度或者说色调遭到了损失。

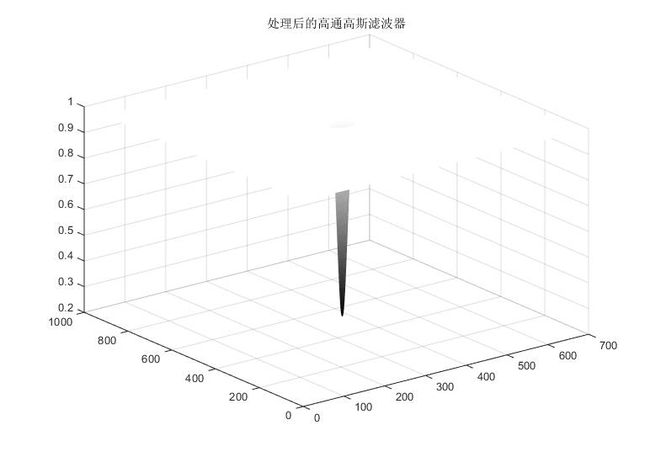
这里我们可以对滤波器加一个小常数来保留部分直流量，既不会影响尖锐性，也能够保留一定的色调。下面我们通过1-0.75*H达到效果：

H3 = 1-0.75*H;
figure(7)
mesh(X',Y',H3)
title('处理后的高通高斯滤波器')
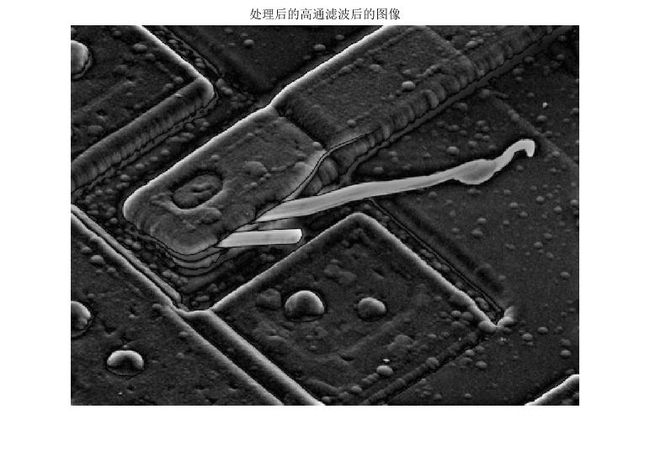
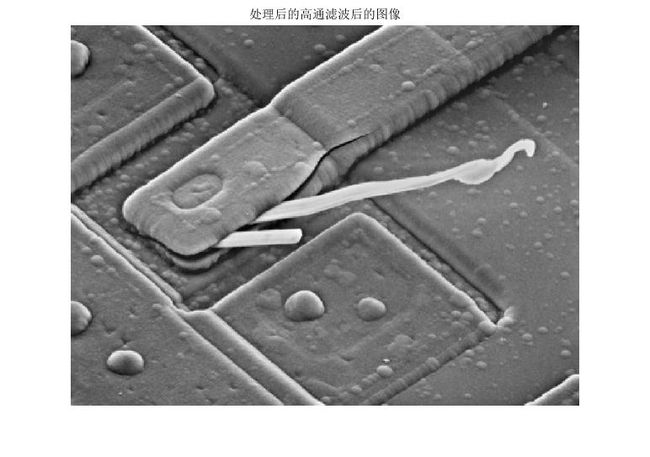
G3 = H3.*Fc;
g3 = ifft2(G3);
g3 = im2uint8(mat2gray(abs(g3)));
figure(8)
imshow(g3)
title('处理后的高通滤波后的图像')

我们可以看到处理后的高通滤波器相对而言保留了一定的色调，若将原点处低频分量设置为1，则变化为，其基本色调保持不变。

这样经低通或高通滤波器处理可以用于图片的模糊或者突出细节，当然我们也可以在此基础上利用上一节的方法，例如非锐化掩蔽的方式对图像进一步处理，这里不做赘述。