深度学习笔记(四)：Cross-entropy损失函数

改进的Cost函数Cross-entropy使神经网络学习更快

---

我们理想的情况是神经网络Cost下降的很快

神经网络是如何学习的

举个例子：一个简单的神经网络模型:只有一个神经元，一个输入一个输出，类似如:

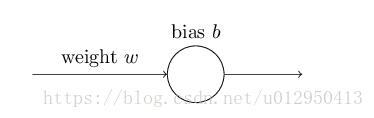
我们使用梯度下降算法来训练这个模型

神经网络学习过程(Cost的变化情况)

假设:输入为1,输出值为0

假设权重 ω ω 我们设置为0.6,初始偏向b设置为0.9，初始预测的输出a=0.82,学习率为0.15,迭代学习300次:

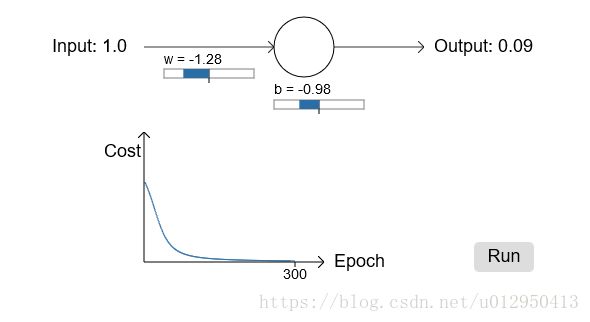
具体演示动画参考

神经网络快速的学习权重和偏向用来降低Cost，虽然最后训练结果和0有些偏差，但是0.09也是很好的结果了

改变初始权重和偏向,预计输出,我们在观察Cost函数的变化情况

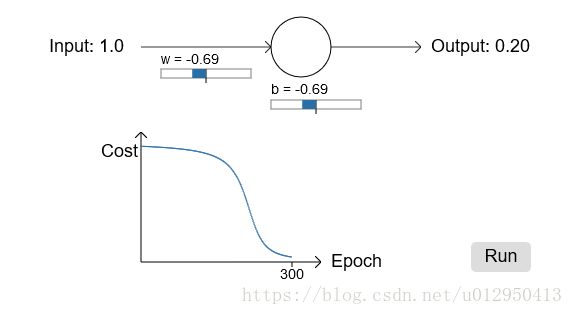
如果我们改变神经元的初始权重和偏向，假设权重 ω ω 我们设置为2.0,初始偏向b设置为2.0，初始预测的输出a= 0.98,学习率为0.15,迭代学习300次:

具体演示动画参考

可以看出Cost函数一开始下降很慢，迭代到200次左右才开始出现明显的下降,而且最后输出值是0.2要比上一个例子0.09差很多。

为什么神经网络会出现一开始学习很慢后来学习变快的情况呢

神经网络学习慢说明了偏导数 ∂C/∂ω ∂ C / ∂ ω 和 ∂C/∂b ∂ C / ∂ b 比较小

回顾之前的Cost函数(二次Cost函数)

C=(y−a)22 C = ( y − a ) 2 2

上式中y是真实输出，a是相应的预测输出， a=σ(z) a = σ ( z ) ,z为中间变量( z=ωx+b z = ω x + b ),分别对 ω ω 和 b b 求偏导

∂C∂w∂C∂b==(a−y)σ′(z)x=aσ′(z)（把x=1,y=0带入）(a−y)σ′(z)=aσ′(z),(1)(2) (1) ∂ C ∂ w = ( a − y ) σ ′ ( z ) x = a σ ′ ( z ) （把x=1,y=0带入） (2) ∂ C ∂ b = ( a − y ) σ ′ ( z ) = a σ ′ ( z ) ,

回顾下一开始用的激活函数sigmoid函数

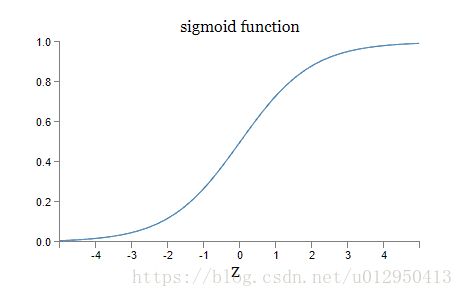
学习速度取决于 aσ′(z) a σ ′ ( z ) ,而 a a 在{0,1}之间，所以 a a 对学习速度影响较小。从图像中可以看出在神经元输出接近0或1的时候，曲线变的很平缓,这个时候 σ′(z) σ ′ ( z ) 小，所以学习速度很慢。

二次Cost函数的缺点

当神经元输出值接近0或1的时候，学习速度很慢，学习的速度跟参数的选择关系很大。

介绍cross-entropy 损失函数（cost function）

使用一个更加复杂的神经网络:
他有一个神经元，三个输入，一个输出

如图 α=σ(z),其中z=∑jwjxj+b α = σ ( z ) , 其中 z = ∑ j w j x j + b

定义新的损失函数cross-entropy如下：

C=−1n∑x[ylna+(1−y)ln(1−a)](3) (3) C = − 1 n ∑ x [ y ln ⁡ a + ( 1 − y ) ln ⁡ ( 1 − a ) ]

把 α=σ(z) α = σ ( z ) 带入上式:

C=−1n∑x[ylnσ(z)+(1−y)ln(1−σ(z))](4) (4) C = − 1 n ∑ x [ y ln ⁡ σ ( z ) + ( 1 − y ) ln ⁡ ( 1 − σ ( z ) ) ]

分别对 ω和b ω 和 b 求偏导:

对 ω ω 求偏导

∂C∂wj===−1n∑x(yσ(z)−(1−y)1−σ(z))∂σ∂wj−1n∑x(yσ(z)−(1−y)1−σ(z))σ′(z)xj−1n∑xσ′(z)xjσ(z)(1−σ(z))(σ(z)−y)(合并同类项)(5)(6)(7) (5) ∂ C ∂ w j = − 1 n ∑ x ( y σ ( z ) − ( 1 − y ) 1 − σ ( z ) ) ∂ σ ∂ w j (6) = − 1 n ∑ x ( y σ ( z ) − ( 1 − y ) 1 − σ ( z ) ) σ ′ ( z ) x j (7) = − 1 n ∑ x σ ′ ( z ) x j σ ( z ) ( 1 − σ ( z ) ) ( σ ( z ) − y ) (合并同类项)

根据sigmoid函数 σ(z)=1/(1+e−z) σ ( z ) = 1 / ( 1 + e − z ) ,对它求导得出 σ′(z)=σ(z)(1−σ(z)) σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) 带入上式得出:

∂C∂wj=1n∑xxj(σ(z)−y)=1n∑xxj(a−y)(1) (1) ∂ C ∂ w j = 1 n ∑ x x j ( σ ( z ) − y ) = 1 n ∑ x x j ( a − y )

对b求偏导

∂C∂b=1n∑x(σ(z)−y)=1n∑x(a−y)(2) (2) ∂ C ∂ b = 1 n ∑ x ( σ ( z ) − y ) = 1 n ∑ x ( a − y )

由(1)(2)两个式可以知道:
学习的快慢(即偏导数的大小)取决于a-y,即输出层的error

cross-entropy函数的好处是:

错误大时,更新多,学得快. 错误小时,学习慢

演示cross-entropy损失函数的学习情况

起始权重为0.6,偏向为0.9，其他都不变

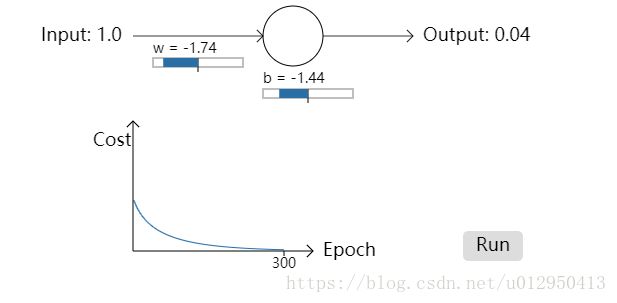
具体演示动画参考
可以看出，cross-entropy cost函数在一开始就学习的很快（曲线下降的很快），而且最后预测输出为0.04,非常接近0，比之前的二次Cost的效果（0.09）好很多。

起始权重和偏向都设置为2.0

具体演示动画参考

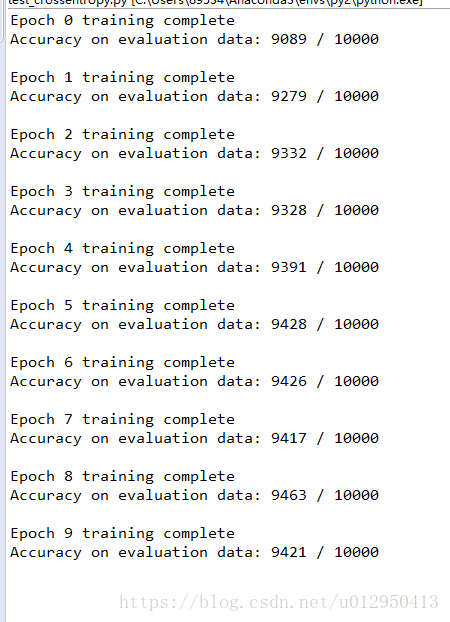
用cross-entropy进行手写数字识别

依然沿用之前的程序

#coding=utf-8
'''
Created on 2018年5月14日

@author: devkite
'''
import mnist_loader
import network2
# cross-entropy损失函数test效果
# cross-entropy不会出现学习缓慢的问题，而且相对二次Cost，学习效果更好
#加载数据集
trainDataset,validationDataset,testDataset = mnist_loader.load_data_wrapper()
# 损失函数使用Cross-entropy
net=network2.Network([784,30,10], cost=network2.CrossEntropyCost)
#初始化权重和偏向，和之前初始化方式是一样的,因为在后面章节将会介绍新的初始化方法，所以在这里改了个名字
net.large_weight_initializer()
net.SGD(trainDataset, 30, 10, 0.5,evaluation_data=testDataset, monitor_evaluation_accuracy=True)

程序效果:

学习效果比之前明显加快

参考代码及我的笔记

总结:

cross-entropy cost几乎总是比二次cost函数好
果神经元的方程是线性的, 用二次cost函数 (不会有学习慢的问题)