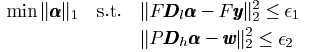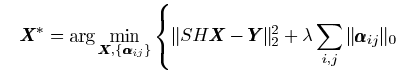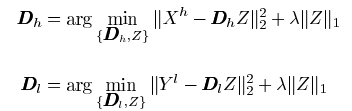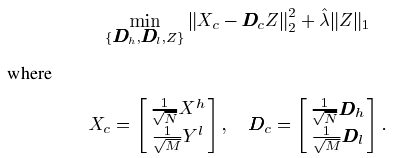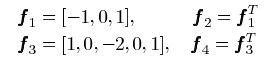Image super-resolution via sparse representation论文总结

• 摘要：

     本文提出了一个基于单幅图像的超分辨率重建。图像可以被表示为一个稀疏线性组合和过完备字典的形式。所以本文提出了将计算得到的低分辨率图像的图像块的稀疏表示系数用于作为高分辨率图像的稀疏表示系数。

• 介绍：

     1、常规的超分辨重建方法：

        （1）输入同一场景的多幅低分辨率图像，调整亚像素精度。（？？？）

        （2）基于插值的方法

        （3）基于机器学习的方法（看几篇机器学习论文和深度学习结合在一起做实验）

     2、 本文工作：

          由高分辨率信号可以由观测到的低维信号恢复得到启发，提出高分辨率图像也可以由低分辨率图像恢复。（从信号到图像）

• Image  SR from sparsity：

    1、给一个低分辨率图像恢复高分辨率图像，需要解决两个问题

        （1）重建约束

                                         Y=SHX

         H代表模糊滤波器，S是采样器，Y是低分辨率图像，X是高分辨率图像。给一个低分辨率图像Y，很多X满足上式，所以通过X的小块x进一步调整问题。

         (2)高分辨率图像X的块x可以由稀疏线性组合表示如下：

                                        

          稀疏表示可以由低分辨率图像Y的块y得到。

      2、普通图像的超分辨率重建

         （1）稀疏表示的局部模型  

               对于每个低分辨率图像块y。可以得到一个对于字典的稀疏表示，由对应的高分辨率图像块的字典可以得到高分辨率图像块x，所以这个问题可以被表示为

                              

               F是一个特征提取算子，F的作用是？？？？？？？？？？？？？

      通过替换为最小化L1范数，可以得到    

                        

    由拉格朗日乘子法求解上述问题                  

     

                    

   独立的解决上述问题不能保证相邻块间的兼容性，所以使用one-pass算法处理兼容性。块用光栅扫描处理，从左到右，从上到下。修改公式为块y的高分辨率重建被相邻高分辨率块约束。得到公式如下

                      （理解为增加了约束）

 矩阵P提取了当前重建的高分辨率块和之前重建的高分辨率块之间的重叠部分，w包含重叠部分的像素值。上式可以 表示为如下形式

                    

    其中参数用来权衡高分辨率图像和低分辨率图像的一致性。参数的作用？？？

 （2）全局重建的约束增强        

      本文设为1.解得最优解为，所以高分辨率图像可以重建为

                                             

      公式和并不能完全使得低分辨率图像块y和重建图像相等。再加上噪声的影响，通过稀疏表示产生的高分辨率图像X0可能不满足约束（2），所以为了消除X0到SHX=Y解空间的矛盾，计算公式。为什么通过这个公式就能消除矛盾和X0有什么关系

                              

  使用梯度下降法解该问题。

  上述过程算法如下：

                              

    （3）全局优化解释（没看懂这一部分）

     给足够的计算资源，系数可以和所有的块联系在一起。高分辨率图像X可以作为一个变量，而不是要求由稀疏系数完美再      现，我们可以惩罚X 和重建图像之间的不同。允许解不是稀疏的。（实验得到好的结果做出的解释？）得到目标函数

               

     这里，表示表示系数，是投影矩阵。 是一种惩罚函数，可以对关于高分辨率图像的其他先验知识进行编          码。 这个函数可以取决于图像类别，或者可以采用通用正则化术语的形式。

       算法1可以被解释为对上述公式的计算有效的近似。然而，算法1并没有包含任何先验，除了表示系数的稀疏性，这个术 语在我们的近似中不存在。 在第四部分中，我们会看到，在相关字典中的稀疏性足够强大时我们已经可以实现良好的SR性能。 尽管如此，在对高分辨率信号进行进一步假设的环境中，这些先验可以融入我们算法的全局重建步骤。

•  学习字典对

   (1）单一字典训练

                

（2）联合字典训练

   同时训练高分辨率图像和低分辨率图像，得到字典。

   独立的函数是

                        

   联合在一起得到目标函数

                  

   M和N是代表高分辨率和低分辨率图像的维度。1/N和1/M是为了平衡成本因子。

  进一步处理得到

                      

   因此可以使用单一字典对的训练策略对上式进行训练。

（3）低分辨率图像块的特征表示  

      F是特征提取算子。F被选为高通滤波。因为人们是更敏感的对于高频图像（查看一些图像关于不同频率的）。

     在本文中，使用first and second-order derivatives作为低分辨率图像块的特征。使用4个1-D滤波器

                            

得到4个maps,联合得到特征向量。