现代控制工程（三）状态方程的解

非齐次状态方程的解——控制工程的受控运动

当线性定常系统
$$\{\begin{array}{c}\dot{x}=Ax+Bu\\ y=Cx+Du\end{array},x(t_0)=x(0)$$的外加输入函数$u(t)̸=0$时，$u(t)$作用下的运动称为可控系统的受控运动。此时状态方程为非齐次矩阵微分方程，即
$$\dot{x}=Ax+Bu,x(t){|}_{t=t_0}=x(t_0),B̸=0$$
式中，x为n维状态向量，u为r维输入向量，A为n*n常系数矩阵，B为n*r常系数矩阵。
求解非齐次状态方程的方法和求解齐次状态方程的方法一致，即 直接法和 拉氏变换法。

直接法

直接法就是按照常数方程求解微分方程的办法来。
改写方程形式为：
$\dot{x}-Ax=Bu$
上式两边同时左乘$e^{-At}$得：
$e^{-At}[\dot{x}-Ax]=e^{-At}Bu$

$\frac{\mathrm{d}}{\mathrm{d}t}[e^{-At}x]=e^{-At}Bu$
对两边的式子进行积分，
${\int }_{t_0}^t\frac{\mathrm{d}}{\mathrm{d}\tau }[e^{-A\tau }x(\tau )]\mathrm{d}\tau ={\int }_{t_0}^t{e}^{-A\tau }Bu(\tau )\mathrm{d}\tau$
可得：$e^{-At}x(t)-e^{-A{t}_0}x(t_0)={\int }_{t_0}^t{e}^{-A\tau }Bu(\tau )\mathrm{d}\tau$
所以：$x(t)=e^{A(t-t_0)}x(t_0)+{\int }_{t_0}^t{e}^{A(t-\tau )}Bu(\tau )\mathrm{d}\tau$
用状态转移矩阵表示为：
$$x(t)=\varphi (t,t_0)x(t_0)+{\int }_{t_0}^t\varphi (t,\tau )Bu(\tau )\mathrm{d}\tau$$
等式右边是两项相加，前一项是初始状态引起的响应，即零输入响应。后一项是输入引起的响应,零状态响应。

上式表明非齐次状态方程的解包含两部分：
①由初始状态引起的状态转移分量，这是自由运动结果；
②由控制作用引起的受控分量，它是受控运动（或称强迫运动）的结果。

拉氏变换法

对齐次状态方程组两边进行拉氏变换得：
$sX(s)-X(0)=AX(s)+BU(s)$
$\Rightarrow (sI-A)X(s)=X(0)+BU(s)$
$\Rightarrow X(s)=(sI-A{)}^{-1}X(0)+(sI-A{)}^{-1}BU(s)$
再进行拉式反变换得：
$x(t)=L^{-1}[(sI-A{)}^{-1}]x(0)+L^{-1}[(sI-A{)}^{-1}BU(s)]$
由方程解的唯一性(直接法和拉式变换法的结果是一致的)可得到：
$e^{A(t-t_0)}=L^{-1}[(sI-A{)}^{-1}]$
${\int }_{t_0}^t\varphi (t,\tau )Bu(\tau )\mathrm{d}\tau =L^{-1}[(sI-A{)}^{-1}BU(s)]$
若$y(t)=Cx(t)+Du(t)$，并且初始时刻为$t_0$
则输出为：
$y(t)=C{e}^{A(t-t_0)}x(t_0)+C{\int }_{t_0}^t\varphi (t,\tau )Bu(\tau )\mathrm{d}\tau +Du(t)$

例题1

这里可以有多种方法求矩阵指数函数，包括定义法根据级数求以及拉式变换法等方法，见 https://blog.csdn.net/weijifen000/article/details/83099396#_58 。

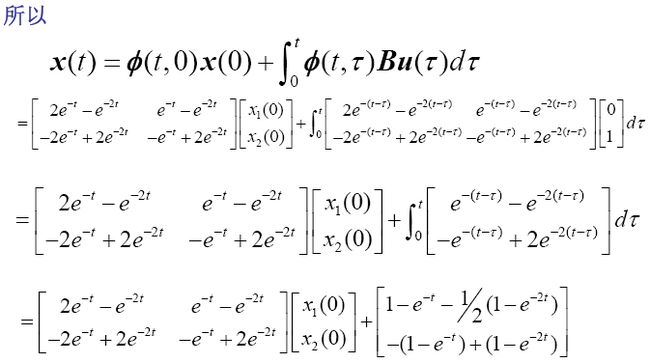
例题2

对于典型输入信号，如单位脉冲、单位阶跃、单位速度等信号作用下，系统的响应（即非齐次状态方程的解）有以下表达式：

1. 单位冲激信号$u(t)=\delta (t)$：
   $x(t)=e^{At}x(0)+e^{At}B$
2. 单位阶跃信号$u(t)=1(t)$：
   $x(t)=e^{At}x(0)+e^{At}B$
3. 速度信号$u(t)=t$：
   $x(t)=e^{At}x(0)+[A^{-2}(e^{At}-I)-A^{-1}t]B$

线性时变系统的运动分析

即系统随着时间变化。
线性时变系统方程为：
$$\{\begin{array}{c}\dot{x}(t)=A(t)x(t)+B(t)u(t)\\ y(t)=C(t)x(t)+D(t)u(t)\end{array}$$

如果$A(t),B(t),C(t)$的所有元素在时间区间$[t_0,+\infty ]$上均是连续函数，则对于任意初始状态$x(t_0)$和输入向量$u(t)$，系统状态方程的解存在并且唯一。

线性时变齐次状态方程的解

线性时变齐次状态方程$\dot{x}(t)=A(t)x(t)$
其解为：$x(t)=\varphi (t,t_0)x(t_0)$
$\varphi (t,t_0)$为状态转移矩阵，具有以下性质：

1. 满足其状态方程本身，即将线性时变齐次状态方程的解带入得到：
   $\frac{\mathrm{d}}{\mathrm{d}t}\varphi (t,t_0)=A(t)\varphi (t,t_0)$
   且初始条件$\varphi (t_0,t_0)=I$
2. 可逆性：
   ${\varphi }^{-1}(t,t_0)=\varphi (t_0,t)$
3. 传递性：
   $\varphi (t_2,t_1)\varphi (t_1,t_0)=\varphi (t_2,t_0)$
4. $\varphi (t,\tau )$对第二变元$\tau$的偏导数为
   $\frac{\mathrm{d}}{\mathrm{d}t}\varphi (t,\tau )=-\varphi (t,\tau )A(\tau )$

状态转移矩阵的计算-级数近似法

$$\begin{gathered} \varphi (t,t_0)=e^{{\int }_{t_0}^{t}A(\tau )\mathrm{d}\tau } \\ =I+{\int }_{t_0}^{t}A({\tau }_0)\mathrm{d}{\tau }_0+{\int }_{t_0}^{t}A({\tau }_0){\int }_{t_0}^{{\tau }_0}A({\tau }_1)\mathrm{d}{\tau }_1\mathrm{d}{\tau }_0 \\ +{\int }_{t_0}^{t}A({\tau }_0){\int }_{t_0}^{{\tau }_0}A({\tau }_1){\int }_{t_2}^{{\tau }_0}A({\tau }_2)\mathrm{d}{\tau }_2\mathrm{d}{\tau }_1\mathrm{d}{\tau }_0+\cdots \end{gathered}$$

例题：

当满足可交换条件时，时变系统状态转移矩阵的解可以表示为：
$$\varphi (t,t_0)=e^{{\int }_{t_0}^{t}A(\tau )\mathrm{d}\tau }$$

例题

线性时变齐次状态方程的解

对于线性时变非齐次状态方程：
$\dot{x}=A(t)x+B(t)u,x(t){|}_{t=0}=x(t_0)$
其解为:
$x(t)=\varphi (t,t_0)x(t_0)+{\int }_{t_0}^t\varphi (t,\tau )B(\tau )u(\tau )\mathrm{d}\tau$
或：
$x(t)=\varphi (t,t_0)[x(t_0)+{\int }_{t_0}^t\varphi (t,\tau )B(\tau )u(\tau )\mathrm{d}\tau ]$
系统输出为：
$y(t)=C(t)\varphi (t,t_0)x(t_0)+C(t){\int }_{t_0}^t\varphi (t,\tau )B(\tau )u(\tau )\mathrm{d}\tau +D(t)u(t)$
或：
$y(t)=C(t)\varphi (t,t_0)[x(t_0)+{\int }_{t_0}^t\varphi (t,\tau )B(\tau )u(\tau )\mathrm{d}\tau ]+D(t)u(t)$

例题