蚁群算法的简单应用
一、概念
蚁群系统(Ant System(AS)或Ant Colony System(ACS))是由意大利学者Dorigo、Maniezzo等人于20世纪90年代首先提出来的。他们在研究蚂蚁觅食的过程中,发现蚁群整体会体现一些智能的行为,例如蚁群可以在不同的环境下,寻找最短到达食物源的路径。
后经进一步研究发现,这是因为蚂蚁会在其经过的路径上释放一种可以称之为“信息素(pheromone)”的物质,蚁群内的蚂蚁对“信息素”具有感知能力,它们会沿着“信息素”浓度较高路径行走,而每只路过的蚂蚁都会在路上留下“信息素”,这就形成一种类似正反馈的机制,这样经过一段时间后,某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大。整个蚁群就会沿着最短路径到达食物源了。
这种算法具有分布计算、信息正反馈和启发式搜索的特征,本质上是进化算法中的一种启发式全局优化算法。
蚁群算法是一种用来寻找优化路径的概率型算法。
二、应用
求解TSP问题
TSP问题:已给一个n个点的完全图,每条边都有一个长度,求总长度最短的经过每个顶点正好一次的封闭回路。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
蚁群算法原理
蚂蚁在路径上释放信息素,当蚂蚁碰到还没走过的路口,就随机挑选一条路走,同时,释放与路径长度有关的信息素,信息素的浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时,蚂蚁在选择下一个要转移的城市时候是基于概率选择的,选择信息素浓度较高路径,最优路径上的信息素浓度越来越高,最终蚁群找到最优寻食路径。
蚁群算法与TSP问题
原理:
将m个蚂蚁随机地放在多个城市,让这些蚂蚁从所在的城市出发,n步(一个蚂蚁从一个城市到另外一个城市为1步)之后返回到出发的城市。如果m个蚂蚁所走出的m条路经对应的中最短者不是TSP问题的最短路程,则重复这一过程,直至寻找到满意的TSP问题的最短路径为止。
路径构建

m:蚂蚁总数,在TSP问题中,每次循环当中,每只蚂蚁所走出的每条路径为TSP问题的候选解,m只蚂蚁一次循环所走出来的m条路经为TSP问题的一个解子集,所以这个解子集越大则算法的全局搜索能力越强,但是过大会使算法的收敛速度降低。如果m太小的话,算法也很容易就陷入局部最优,过早的出现停滞现象。
alpha:信息素重要程度因子,反映了蚂蚁在从城市i向城市j移动时,这两个城市之间道路上所累积的信息素在指导蚂蚁选择城市j的程度,即蚁群在路径搜素中随即性因素作用的强度。alpha值越大,蚂蚁选择之前走过的路径的可能性越大,搜索路径的随机性减弱,alpha越小,蚁群搜索范围就会减小,容易陷入局解最优。
beta:启发函数重要程度因子,beta值越大,蚁群就越容易选择局部较短路径,这时算法的收敛速度是加快了,但是随机性却不高,容易得到局部的相对最优。
tabu:禁忌表,用于存放第k只蚂蚁已经走过的城市。
rho:是信息素挥发因子,规定0≤ rho≤1,1- rho为信息残留因子,rho过小时,在各路径上残留的信息素过多,导致无效的路径继续被搜索,影响到算法的收敛速率,rho过大,无效的路径虽然可以被排除搜索,但是不能保证有效的路径也会被放弃搜索,影响到最优值的搜索,在AS中通常设置为 rho =0.5。
三、实验过程
(1)随机产生50个的城市坐标信息
round(rand(50,2)*4000)+1000
产生的数据
2204 2888
1708 2879
3366 2135
1245 1009
3163 1774
4837 3657
1179 2747
3539 1523
4774 2251
1037 3795
2045 3202
2440 4955
1256 2874
1733 4631
1425 4783
2315 2293
2763 4099
2028 3990
4507 4693
1493 4696
3813 4099
3445 2484
4609 2167
3064 4223
3091 3881
4003 1069
1294 3609
4987 1317
4275 3986
2396 1675
1837 1798
1668 1988
4979 4193
1781 3376
4234 4790
2106 1039
3182 2961
1270 1874
3776 3649
2349 1028
1709 1833
4078 1168
3958 1289
2408 4100
2716 1369
4930 3373
2402 2250
2487 1332
4912 3094
2312 3723
(2)产生的数据放入matlab.mat文件中,从ACO.m中读入
%% 导入数据
load matlab.mat
(3)算法执行过程
%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc
%% 导入数据
load matlab.mat
%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 150; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%% 迭代寻找最佳路径
figure;
while iter <= iter_max
fprintf('迭代第%d次\n',iter);
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
% figure;
%最佳路径的迭代变化过程
[Shortest_Length,index] = min(Length_best(1:iter));
Shortest_Route = Route_best(index,:);
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
pause(0.3);
iter = iter + 1;
Table = zeros(m,n);
% end
end
%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
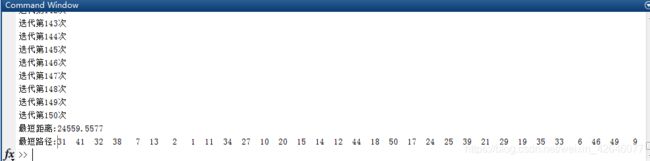
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
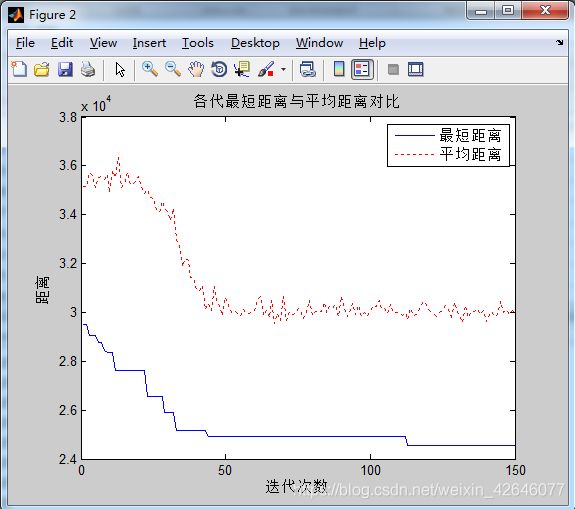
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
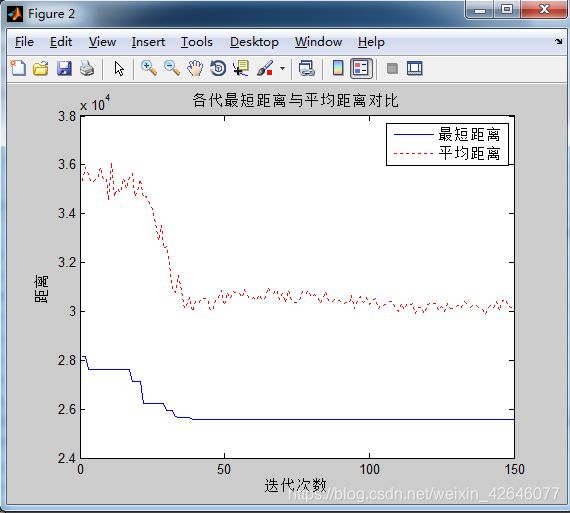
title('各代最短距离与平均距离对比')
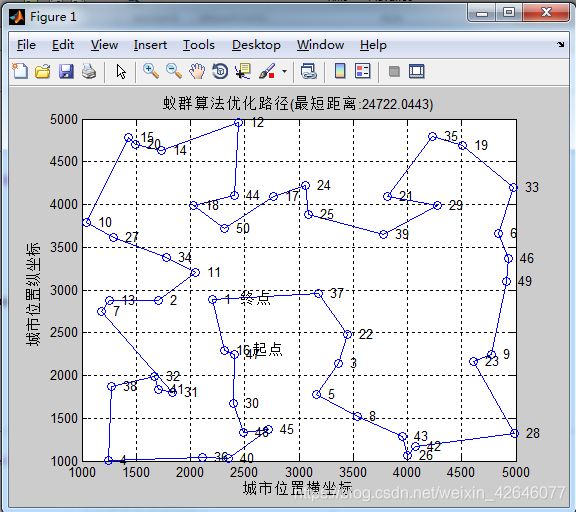
(4)经过150次迭代,对50个城市求最优路径,结果是24722.0443,执行之后的效果图如下:
1.改变rho的值
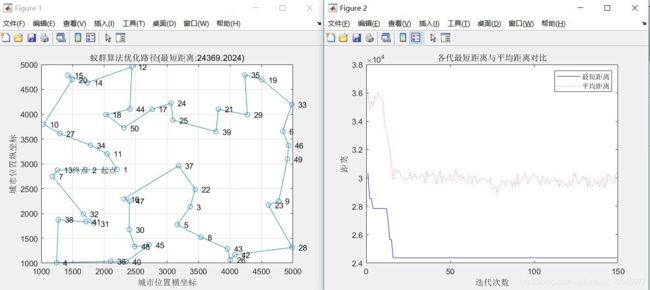
- alpha=1,beta=5,rho=0.1实验结果
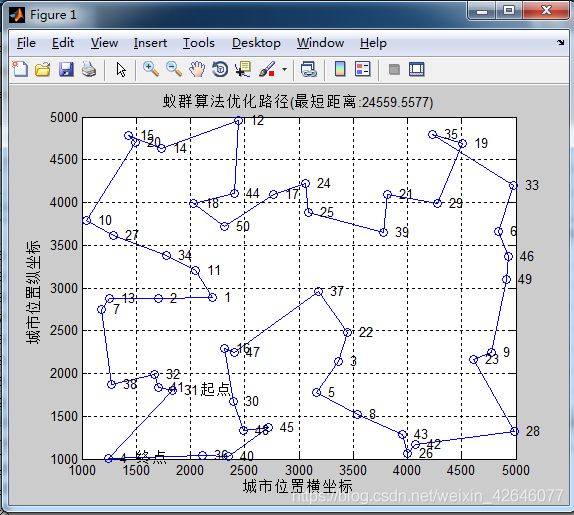
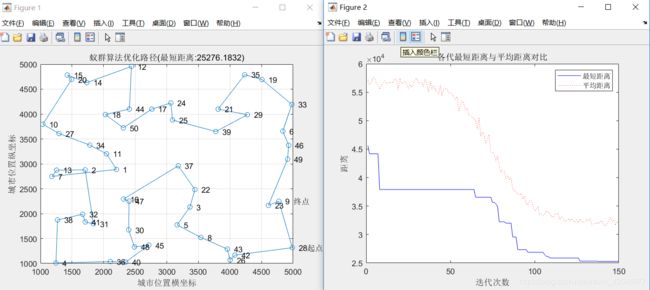
- alpha=1,beta=5,rho=0.5实验结果
最短距离:24369.2024
最短路径:2 1 11 34 27 10 20 15 14 12 44 18 50 17 24 25 39 21 29 35 19 33 6 46 49 9 23 28 42 26 43 8 5 3 22 37 16 47 30 48 45 40 36 4 38 41 31 32 7 13 2
- alpha=1,beta=5,rho=0.8实验结果
最短距离:24509.4447
最短路径:35 19 33 6 46 49 9 23 28 42 26 43 8 5 3 22 37 47 16 30 48 45 40 36 4 38 32 41 31 7 13 2 1 11 34 27 10 20 15 14 12 44 18 50 17 24 25 39 21 29 35
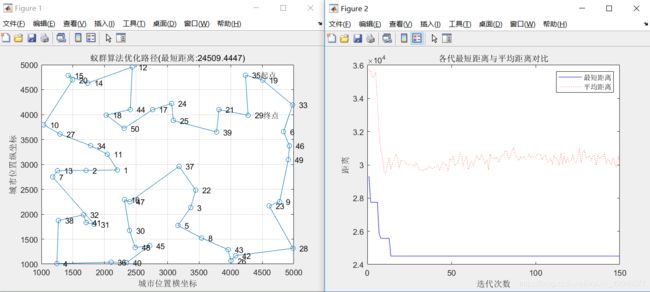
(2)改变alpha的值
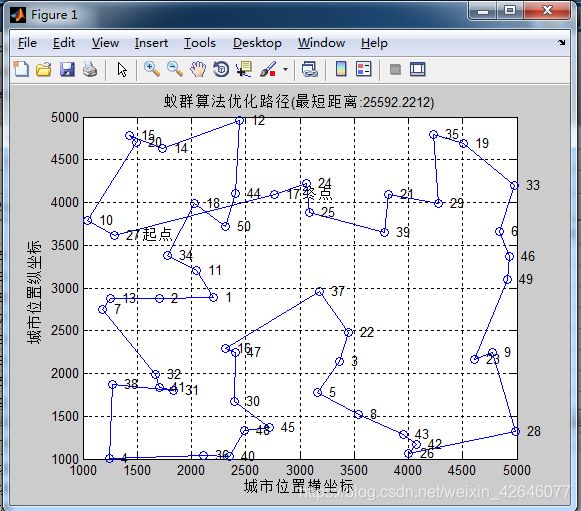
- alpha=2,beta=5,rho=0.1的实验结果: 最短距离变成:25592.2212
- alpha=5,beta=5,rho=0.1的实验结果:
最短距离:25005.9738
最短路径:37 22 3 5 8 43 42 26 28 23 9 49 46 6 33 19 35 29 21 39 17 24 25 50 18 44 12 14 20 15 10 27 34 11 1 2 13 7 41 31 32 38 4 36 40 48 45 30 47 16 37
- alpha=8,beta=5,rho=0.1的实验结果:
最短距离:24857.26
最短路径:44 17 24 25 39 21 29 19 35 33 6 46 49 9 23 28 42 26 43 8 5 3 22 37 16 47 30 48 45 40 36 4 38 32 41 31 7 13 2 1 11 34 27 10 20 15 14 12 50 18 44
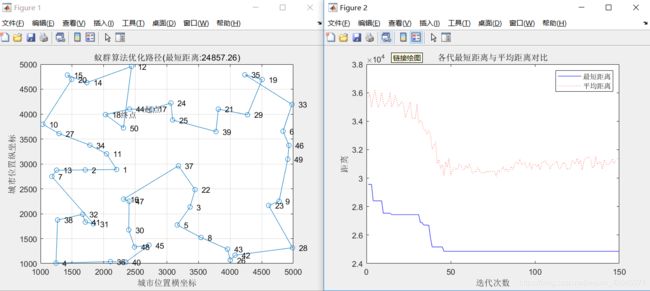
(3)改变beta的值
alpha=1,beta=2,rho=0.1的实验结果:
最短距离:25276.1832
最短路径:28 42 26 43 8 5 3 22 37 16 47 30 48 45 40 36 4 38 32 41 31 2 13 7 1 11 34 27 10 20 15 14 12 44 18 50 17 24 25 39 29 21 35 19 33 6 46 49 23 9 28
- alpha=1,beta=8,rho=0.1的实验结果:
最短距离:24715.6651
最短路径:12 14 20 15 10 27 34 11 1 2 13 7 38 32 41 31 4 36 40 48 45 30 47 16 37 22 3 5 8 43 42 26 28 9 23 49 46 6 33 19 35 21 29 39 25 24 17 44 18 50 12
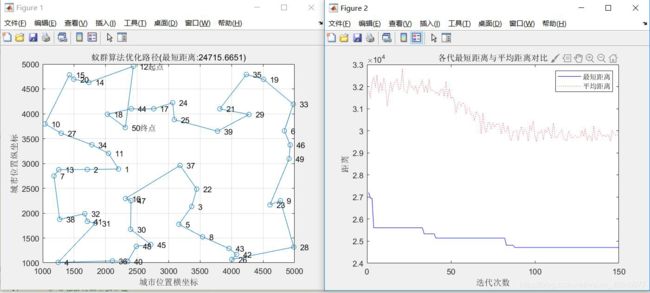
实验结果分析

在这次实验中通过改变信息素挥发因子rho和信息素重要程度因子alpha和启发函数重要程度因子beta的大小,观察最短路径的大小来比较它们对产生最优解的影响。
1.当把rho从0.1->0.2->0.5的过程中,最短路径的大小在减小,rho是信息素挥发因子,rho值过小时,信息素的残留越多,导致过多的无效搜索。当增大其至0.5时最短路径减小,是个优化过程。
2.当把alpha改成2->5->8时,蚂蚁选择之前走过路径的可能性越大,导致最短路径大小减小,对于本次实验,也是个优化过程。
3.把beta从2->5->8的过程中,最短路径在beta=5时取得最小值。4
4.在本次实验中,第四组为最优解,其中alpha=1,bata=5,rho=0.5。