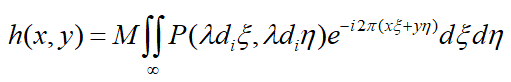光学成像系统的模型及MATLAB仿真
光学成像系统的模型及MATLAB仿真
本文将给出相干成像系统、非相干成像系统模型，以及像差对成像系统影响的模型，模型和相关概念主要参考goodman的《傅里叶光学》。
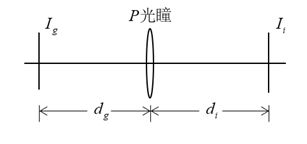
一、相干成像系统
相干成像系统对于振幅来说是线性空间不变系统，存在关系：
其中h(x,y)为点扩展函数，放大倍数M=-di/dg，点扩展函数表达式为：
对应的相干光学传递函数(CTF)为：
一般不考虑比例尺，以及光瞳一般为中心对称，所以将CTF表示为:
二、非相干成像系统
非相干成像系统对于强度的传播是线性空不变的，所以存在
由傅里叶定理可知，像强度的频谱等于物强度频谱与传递函数乘积：
因为人眼或者仪器对图像的视觉效果取决于像所携带信息与直流背景的相对比值，所以利用零频分量对频谱归一化：
所以经代入化简得到光学传递函数(OTF)为：
频谱是复数，可将OTF表示为：
它的模称为调制传递函数(MTF)，幅角称为位相传递函数。
OTF的计算
如果P(x,y)只取值0和1，那么OTF可理解为
计算OTF的实例
该传递函数会使得高频分量的对比度降低，可进行相应的MATLAB仿真。对几个参数进行初始化，
lamda = 500e-9;
R = 10e-2;
di = 50e-2;
p0 = 2*R/lamda/di %截止频率
fX = linspace(-10e5,10e5,2000);
fY = linspace(-10e5,10e5,2000);
[fx,fy] = meshgrid(fX,fY); 可以绘制出圆孔的OTF为：
图1 圆孔的光学传递函数
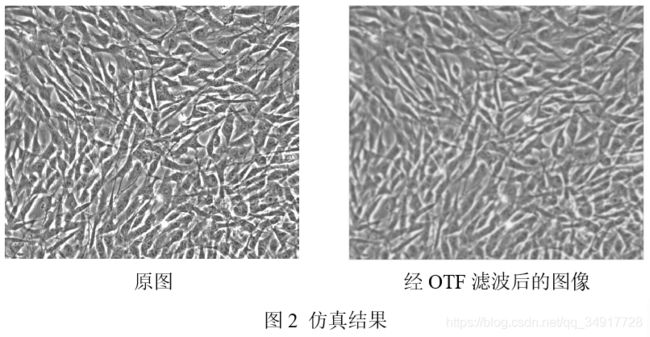
利用这种光学传递函数模拟物体图像经过成像系统之后的成像情况。
设置OTF的截止频率为原图的最大频率的一半，得到如下结果：
三、像差对系统的影响
像差引起了波面的变形（产生波像差），所以像差的存在可表示为在光瞳函数上增加一位相偏差：
聚焦误差是的OTF
若光瞳是矩形，此时OTF为：
不同的W_M对OTF有不同的影响：
当任何一种像差严重时，可以把几何光学对该系统预言的强度点扩展函数(复振幅传播到对应的像面，再求强度即可)做傅里叶变换以得到OTF的良好近似。
四、对超分辨率的理解
一般将瑞利判据所确定的分辨距离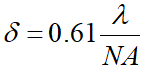
当做是成像系统的最小分辨距离(最大分辨率)。这里的分辨距离是指在成像仪器底片上的分辨距离，所以一般要保证像元尺寸小于δ/2才能完整保存光学衍射产生的最小分辨，在此基础上，如果能够得到超越这一分辨率的实际图像(获得截止频率以外的值)，那么这个过程就实现了超分辨。
因为空间中的物是有界的，在没有噪声时，在原则上是能够分辨出物的无穷小细节的。它具有相关的数学基础：
定理1 一个空间有界函数的二维傅里叶变换是(f_x,f_y)平面上的解析函数。
定理2 (f_x,f_y)平面上一个任意的解析函数，若在此平面上的一个任意小(但有限)的区域内精确知道这个函数的值，那么整个函数可通过解析延拓手段唯一地定出。
因此实际拍摄到的图片并非没有包含截止频率以外的信息，它的辛格函数的延伸包含在通带内(信号较弱)，因此是有可能复原出通带之外的频谱的。
实现超分辨的方法包括基于频率域中的抽样定理的方法；基于长椭球波函数展开式的方法；以及一种适合与数字设备的迭代方法(与GS算法类似)，它逐次加强空域和频域中的约束。
附录: OTF的仿真程序
成像中的图片可以自己找一幅图，记得变换为灰度图像，circ是圆域函数(见主程序后面)
clc,clear
close all
%initial
lamda = 500e-9;
R = 10e-2;
di = 50e-2;
p0 = 2*R/lamda/di %截止频率
%read the image
I = imread('细胞.jpg');
figure(1),imshow(I);
I = double(I);
[Nx,Ny] = size(I);
p0 = max(fix([Nx,Ny]/2));
fX = [0:fix(Nx/2),ceil(Nx/2)-1:-1:1];%linspace(-10e5,10e5,2000);
fY = [0:fix(Ny/2),ceil(Ny/2)-1:-1:1];%linspace(-10e5,10e5,2000);
[fx,fy] = meshgrid(fY,fX);
%OTF
p = sqrt(fx.^2+fy.^2);
f =@(fx,fy) 2/pi*(acos(p./p0)-p./p0.*sqrt(1-(p/p0).^2)).*circ(fx,fy,p0);
H0 = f(fx,fy);
%mesh(fx,fy,H0)
%simulation
F_I = fft2(I); %物强度频谱
G0 = F_I(1,1);
R_I = F_I/G0; %归一化
R_i = R_I.*H0*G0;
i = ifft2(R_i);
figure(2),imshow(uint8(i));其中circ函数定义如下：
function z = circ(x, y, R)
% function z = circ(x, y, D)
r = sqrt(x.^2+y.^2);
z = double(r