(萌新第一次发文,请大佬指正)
要了解树状数组,首先需要了解它是用来做什么的.
那么:
树状数组的问题模型
- 单点维护,区间查询(PUIQ问题)
- 区间维护,单点查询(IUPQ问题)
- 求逆序对问题
先来了解一下树状数组的逻辑模型
如图: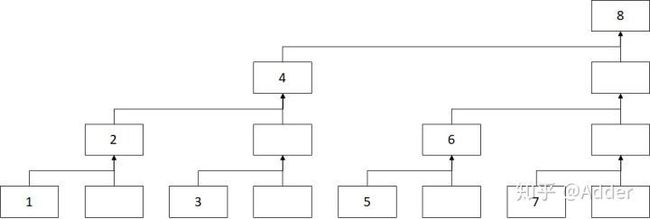
突然一看可能难以理解,那么是什么把它们联系起来的呢?
接下来介绍lowbit函数
lowbit(求二进制数最后一位1的位置)
这里用到了补码的原理:
即负数的补码为其二进制绝对值取反+1,而当其与其绝对值取&操作时得到的恰好就是其二进制最后一位1的位置
例如:00001000(8)的负数补码为11111000(-8) 与操作后为00001000
而lowbit(8)的值就为 00001000;
则 lowbit函数代码
inline int lowbit(int x)
{
return x & -x;
}这里就稍微偏个题顺便介绍一下inline(内联函数)
C++关键字,在函数声明或定义中函数返回类型前加上关键字inline,即可以把函数指定为内联函数。
在c/c++中,为了解决一些频繁调用的小函数大量消耗栈空间(栈内存)的问题,特别的引入了inline修饰符,表示为内联函数。
此关键字仅是对编译器的一种建议,并非强制.对于内容较短且无循环的代码,inline的使用可以增加函数运行的效率,但其效率的增加是以代码长度为代价,所以,仅在短且无循环的函数前可以使用,其他情况避免使用.
原理
那么lowbit函数的用处是什么呢.
让我们以二进制思维稍微注意一下可以发现,每个序号的二进制数的后导0的个数,恰为其包含的数组的深度(自底向上的),设其为d,那么其包含的范围就是包括它向前的2^d个数.如100(4)为从100向前4个原数组中的数的和,而110(6)是从110向前2个原数组中的数的和.
我们令原数组为a[],树状数组为tree[].
这时,我们可以理解tree数组中存储的到底是什么数据,
那么对于以上问题模型,我们该如何求解呢.
更新(update函数)
我们要更新原数组中某一个数,那么就得更新树状数组中所有包含它的数据,
那么,都有哪组数据包含它呢,也就是寻找这个子节点的所有根节点的特点.
这时,就又轮到我们的lowbit函数上场了,x的所有父节点只需x + lowbit(x)就可以得到.
那么update函数的代码(时间复杂度O(logn)):
//x为需要修改的节点,v为a[x]增加的值,n是树状数组的最大范围.
void update(int x,int v)
{
for(;x <= n;x += lowbit(x))
tree[x] += v;
}查询(query函数)
对于树状数组tree,我们可以了解其存储的值实质上是某一区间的前缀和.
我们查询某一段区间(x,y)的值,就只需要求出y的前缀和减去x-1的前缀和
这样得到的,就是区间(x,y)的和.
那么(1,x)区间的前缀和怎么求呢,仍然是lowbit函数,只需要做一遍更新的逆过程,
即计算tree数组(x->1)的和就可以求出所有不重合的区间前缀和.
为什么tree(x->1)就是该区间的前缀和?
在二进制的视角下,x的数位上每一个1,都代表其一段域内的值,
那么,每个1都必然与其他1的范围不重合例如:tree[110] = tree[100] + tree[10]
如此,query的代码就很明了了.
int query(int x)
{
int res = 0;
for(;x > 0;x -= lowbit(x))
res += tree[x];
return res;
}板子题链接(luoguP3374)
到此为止,我们讲解的就是PUIQ模型,即点更新,段查询.
怎么样代码是不是短到怀疑人生,这在赛场上写起来不是舒舒服服?
那么,接下来的IUPQ模型,就需要一个切入点来完成操作了.
IUPQ模型的解题切入点---差分
当我们想要进行段更新时,那么如果仍然用上面的代码,就不得不添加一个for循环,
此时update函数的时间复杂度会上升到O(nlogn),那么,有没有什么方法来优化操作呢?解决方案就是--差分
差分,也就是定义一个差分数组b来存储a数组的差值,而tree作为数组b的树状数组.
即:
b[1] = a[1]
b[2] = a[2] - a[1]
b[4] = a[4] - a[1]
tree[1] = b[1]
tree[2] = b[2] + tree[1]
tree[4] = tree[2] + tree[3] + b[4]那么这时的a数组值该如何得到呢?
对于b数组,a[n]就等于b[1] +...+b[n]
而query函数刚好就是用来求b[n]的前缀和,也就是a[n]的值.
那么更新操作呢,对于差分数组b,若我们想要更新[l,r]范围内的值+v,那么我们只需要将b[l]更新为b[l] + v就代表着a[l] - a[n]所有数都+1,
而在b[r+1]处将+v的效果消除,即b[r+1] - v
那么如何将这个操作更新在tree数组中,就是上文update的事情了.
即只需更新b[l]+v,b[r+1]-v即可
update(l,v);
update(r+1,-v);复杂度同样为O(logn)
板子题链接(luoguP3368)
求逆序对问题
问题模型,给定n个整数,求出逆序整数对数(即a[u] > a[v] && u < v的整数对)
看见题目我们就可以写出O(n2)的暴力for来求解,但是如何将其用树状数组来优化到O(nlogn)呢
这里用到桶排序的思想.
首先让问题简单化一点,让n个整数a[i]均小于等于100.
那么我们就可以开tree[105]的数组,每次读入更新一个数时,只需update(a[i],1)
此时,比a[i]大的数字就是需要更新的逆序对对数,即query(a[100]) - query(a[i])因为当前共读入了i个数,那么求值亦可简化为i - query[a[i]]
也就是读入一轮+每次查询就可得到总共的逆序对对数.时间复杂度O(nlogn)
那么当数据足够大时,我们的数组存不下的时候呢,这时候,就轮到我们的核心思想,离散化出场了.
对于离散化,个人理解就是由于想要利用桶数组,故将数据相对缩小(保证相对大小不变)到可以开到的数组那么大而减小空间需求.
那么到底该如何实现,请看如下代码:
离散化核心代码:
struct node
{
int v;//数值本身
int order;//原序列的的下标
}a[500005];
int dis[500005]; //用来存储原数第i个数的order下标是什么
sort(a,a+n,cmp); //注意需要由大到小排
for(int i = 1;i <= n;++i)
dis[a[i].order] = i;原理很简单就只是按a[i].v的大小重排,并重新赋予他们相对大小不变,整体缩小的新的a[i].v
具体代码如下:(HDU2689)
#include
#define mem(n) memset(n,0,sizeof(n))
using namespace std;
int n;
struct node{
int val,order;
bool operator < (const node & x) const{
return this->val < x.val;
}
}a[1005];
int dis[1005]; //差分数组
int tree[1005];
inline int lowbit(int x)
{
return x & -x;
}
void update(int x,int v)
{
for(;x <= n;x +=lowbit(x))
tree[x] += v;
}
int query(int x)
{
int res = 0;
for(;x > 0;x -= lowbit(x))
res += tree[x];
return res;
}
int main()
{
while(~scanf("%d",&n)){
mem(a);
mem(dis);
mem(tree);
for(int i = 1;i <=n;++i){
scanf("%d",&a[i].val);
a[i].order = i;
}
sort(a + 1, a + 1 + n);
for(int i = 1;i <= n;++i){
dis[a[i].order] = i;
}
int cnt = 0;
for(int i = 1;i <= n;++i){
update(dis[i],1);
cnt += i - query(dis[i]);
}
printf("%d\n",cnt);
}
return 0;
}