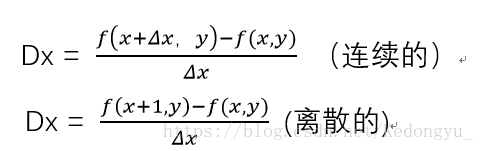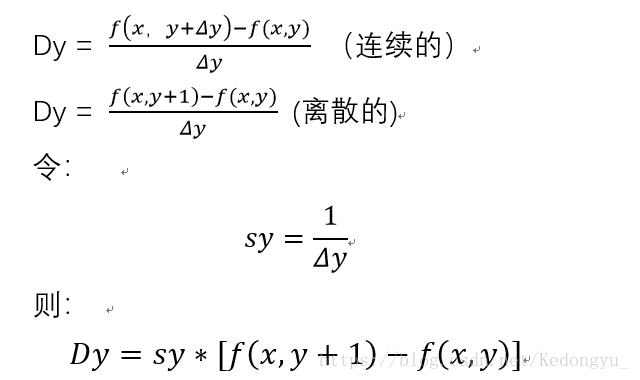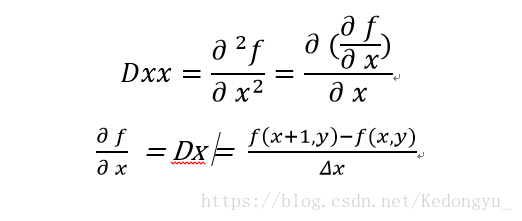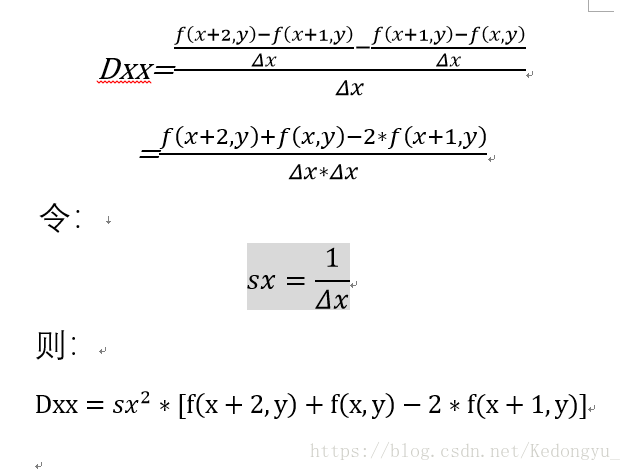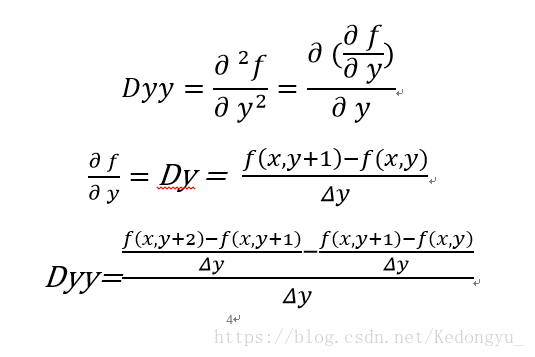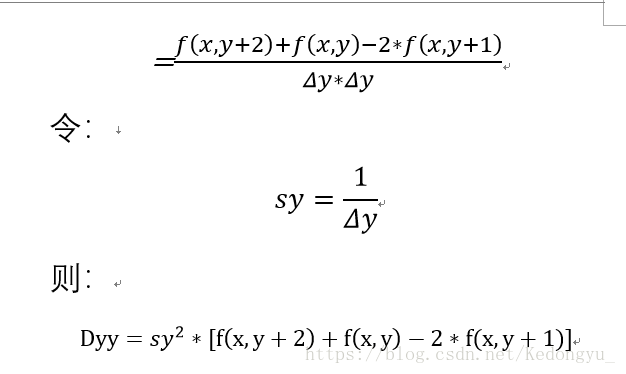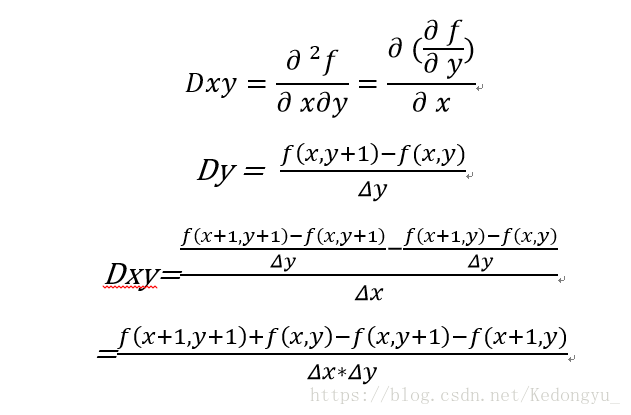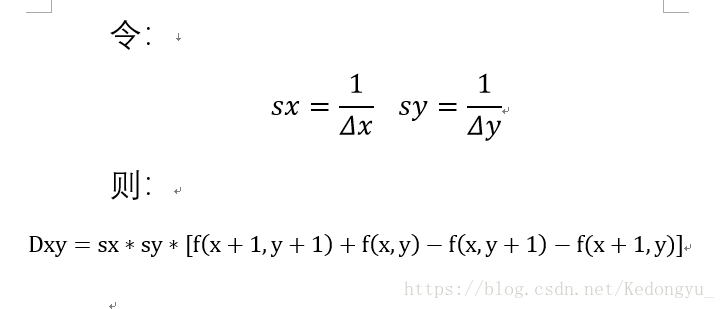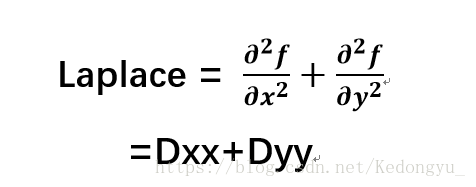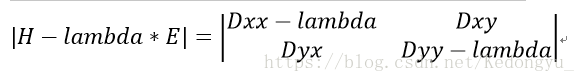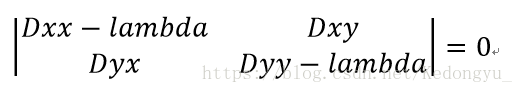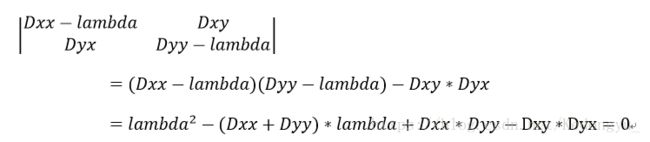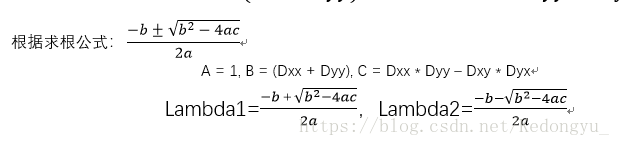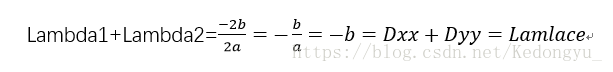图像处理 之 探索 与 验证 拉普拉斯算子（Laplace）与 Hessian矩阵特征值 之间的关系

目录

引言

一、矩阵一阶偏导数

      1. X轴方向

      2. Y轴方向

二、矩阵二阶偏导数

      1. X轴方向上二阶偏导

      2. Y轴方向上二阶偏导

      3.第一次在X轴方向上求偏导，第二次在Y轴方向上求偏导

      4.第一次在Y轴方向上求偏导，第二次在X轴方向上求偏导

      5.结论

三、拉普拉斯算子（Laplace）

四、Hessian矩阵

      1.图像的Hessian矩阵

      2.Hessian矩阵的特征值（2个）

      3.验证推论A

五、代码（全部）

---

引言

      数学：验证矩阵对角线元素和等于特征值之和

      应用而言：给定图像，计算他的Hessian矩阵，Laplace算子 = Hessian矩阵的特征值之和。

      即：Laplace= EigenOfHessian     

 

一、矩阵一阶偏导数

      1. X轴方向

      编写代码：

def gradx(Img, sx = 1.0):          
    return sx * (Img[1: , : ] - Img[ :-1, : ]) 

      2. Y轴方向

      编写代码：

def grady(Img, sy = 1.0):
    return sy * (Img[ : , 1: ] - Img[ : , : -1])

二、矩阵二阶偏导数

      1. X轴方向上二阶偏导

      编写代码：

def gradxx(img, sx = 1.0):
    return sx ** 2 * (img[2 : ] + img[ : -2] - 2 * img[1 : -1])

 

      2. Y轴方向上二阶偏导

      编写代码：

def gradyy(img, sy = 1.0):
    return sy ** 2 * (img[ : , 2: ] + img[ : , :-2] - 2 * img[ : ,1:-1])

 

      3.第一次在X轴方向上求偏导，第二次在Y轴方向上求偏导

      编写代码：

def gradxy(img, sx = 1.0, sy = 1.0):
    return sy * sx * ((img[:-1, :-1]+img[1:,1:])-(img[:-1,1:]+img[1:,:-1]))

      4.第一次在Y轴方向上求偏导，第二次在X轴方向上求偏导

此章节自行验证，可以得出，Dxy与Dyx其结果是一致的。

      5.结论

 

三、拉普拉斯算子（Laplace）

      编写代码：

def laplace(img, sx = 1.0, sy = 1.0):
    return gradxx(img, sx) + gradyy(img, sy)

 

四、Hessian矩阵

      1.图像的Hessian矩阵

根据定义,可知：

      2.Hessian矩阵的特征值（2个）

设lambda为Hessian矩阵的特征值，则该矩阵的特征多项式为：

并且当它为0时有非零解，即:

求解lambda:

      3.验证推论A

 

五、代码（全部）

# -*- coding: utf-8 -*-
"""
Created on Mon Jul  2 15:13:18 2018

@author: Diko
"""
import numpy
from skimage import data,color
def dxx(img ,sx = 1.0):
    return sx**2*(img[2:] + img[:-2] - 2*img[1:-1])

def dyy(img ,sy = 1.0):
    return sy**2*(img[:,2:] + img[:,:-2] - 2*img[:,1:-1])

def dxy(img ,sx = 1.0, sy = 1.0):
    return sx*sy*(img[1:,1:] + img[:-1,:-1] - img[1:,:-1] - img[:-1,1:])

def laplace(img, sx =1.0, sy = 1.0):
    return (dxx(img, sx)[:,:-2] + dyy(img, sy)[:-2,:])

def eigenOfHessian(img, sx = 1.0, sy = 1.0):
    lam = numpy.empty([2, img.shape[0]-2, img.shape[1]-2])
    H11, H12, H21, H22 = dxx(img, sx)[:,:-2], dxy(img,sx,sy)[:-1,:-1], dxy(img, sx,sy)[:-1,:-1], dyy(img, sy)[:-2,:]
    A, B, C = 1, -(H11 + H22), H11*H22 - H12*H21
    de = numpy.sqrt(B**2 - 4*A*C)
    lam1 = (-B + de)/(2*A)
    lam2 = (-B - de)/(2*A)
    lam = lam1, lam2
    return lam

if __name__ == "__main__":
    epsilon = 1e-10
    pictures = [color.rgb2gray(data.chelsea()),color.rgb2gray(data.astronaut()),color.rgb2gray(data.camera())]
    for pic in pictures:
        error = numpy.ones([pic.shape[0]-2,pic.shape[1]-2])*epsilon
        if((numpy.abs(laplace(pic,1.0,1.0)-numpy.sum(eigenOfHessian(pic,1.0,1.0),0))