c++实现图的广度优先搜索(BFS)和深度优先搜索(DFS)

1. 基本概念

1. 图分为无向图和有向图。
2. 与一个顶点相邻接的顶点数叫做该顶点的度。在有向图中，进入一个顶点的弧叫做该顶点的入度，从一个顶点发出的弧叫做该顶点的出度。
3. 在无向图中，若图中任意一对顶点都是连通的，则称此图是连通图。
4. 在有向图中，若任意一对顶点u和v间存在一条从u到v的路径和从v到u的路径，则称此图是强连通图。
5. 无向图的一个极大连通子图称为该图的一个连通分量。
6. 有向图的一个极大强连通子图称为该图的一个强连通分量。
7. 在图的每条边上加上一个数字作权，也称代价，带权的图称网。

关于图的基本概念实在是太多了，大家可以找一本数据结构的书看看，这里也推荐一篇博客可以看看图(1)——图的定义和基本概念

2. 图的表示方式

图基本上有二种表达方式，分别是邻接表和邻接矩阵。数据结构 学习笔记（七）：图（上）：图的表示方法（邻接表，邻接矩阵），遍历（DFS，BFS）

这里我们使用的是邻接表方法。

3. 图的存储结构

class Graph {
 private:
     int V; // vertex num
     std::list<int>* adj;   // adjacency list
 public:
    Graph(int V);
    ~Graph();
    void addEdge(int v, int w);
};

Graph::Graph(int V) {
    this->V = V;
    adj = new std::list<int> [V];   // init adjacency list
}

Graph::~Graph() {
    delete [] adj;  // need [] attention!
    adj = nullptr;
}

void Graph::addEdge(int v, int w) {
    adj[v].push_back(w);
}

int main()
{
    int V(5);
   	Graph g(V);     // create graph
	std::set<int> edgeInput[V];
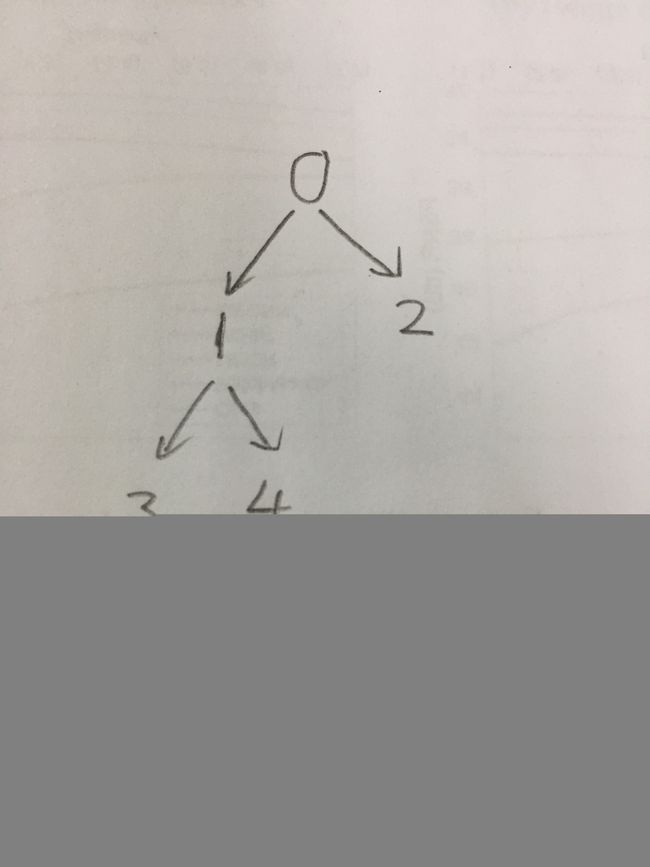
    edgeInput[0].insert({1, 2});
    edgeInput[1].insert({3, 4});
    for (int i = 0; i < V; ++i) {
        for (auto it = edgeInput[i].begin(); it != edgeInput[i].end(); ++it) {
            g.addEdge(i, *it);     // insert edge
        }
    }
 
    return 0;
}

这里的话我们使用邻接表的方法，为了方便我们这里使用STL::list结构，这样话我们使用std::list*就可以实现了整个邻接表的描述，这个比使用二级指针表述邻接表要方便一点。

我们使用以下的有向无环图作为我们的测试例子：

4. 深度优先搜索遍历

首先访问图中某一起始顶点0，然后由0出发，访问与v邻接且未被访问的任一顶点1，再访问与1邻接且未被访问的任一顶点3，……重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止。

DFS本质是一种递归调用，我们可以直接使用递归也可以使用栈来代替递归的过程，同时我们注意需要使用一个visited数组来保存我们的元素是否已经被遍历过了。或者我们也可以使用std::set进行代替。

void Graph::DFSUtil(int v, bool* visited) {
    visited[v] = true;
    std::cout << v << " ";
    for (auto it = adj[v].begin(); it != adj[v].end(); ++it) {
        if (!visited[*it]) {
            DFSUtil(*it, visited);
        }
    }
}

void Graph::DFS() {
    bool* visited = new bool[V];
    for (int i = 0; i < V; ++i) {
        visited[i] = false;
    }
    for (int j = 0; j < V; ++j) {
        if (!visited[j]) {
            DFSUtil(j, visited);
        }
    }
}

5. 广度优先搜索遍历

首先访问起始顶点0，接着由0出发，依次访问0的各个未访问过的邻接顶点1，2，…，，然后再依次访问1，2，…，的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，再访问它们所有未被访问过的邻接顶点……依次类推，直到图中所有顶点都被访问过为止。

广度优先搜索是一种分层的查找过程，每向前走一步可能访问一批顶点，不像深度优先搜索那样有往回退的情况，因此它不是一个递归的算法。为了实现逐层的访问，算法必须借助一个辅助队列，以记录正在访问的顶点的下一层顶点。

void Graph::BFSUtil(int v, bool* visited) {
    std::queue<int> myqueue;
    visited[v] = true;
    myqueue.push(v);
    while (!myqueue.empty()) {
        v = myqueue.front();
        std::cout << v << " ";
        myqueue.pop();
        for (auto it = adj[v].begin(); it != adj[v].end(); ++it) {
            if (!visited[*it]) {
                visited[*it] = true;
                myqueue.push(*it);
            }
        }
    }
}

void Graph::BFS() {
    bool* visited = new bool[V];
    for (int i = 0; i < V; ++i) {
        visited[i] = false;
    }
    for (int j = 0; j < V; ++j) {
        if (!visited[j]) {
            BFSUtil(j, visited);
        }
    }
}

6. 完整代码

#include 
#include 
#include 
#include 

class Graph {
 private:
     int V; // vertex num
     std::list<int>* adj;   // adjacency list
     void BFSUtil(int v, bool* visited);
     void DFSUtil(int v, bool* visited);
 public:
    Graph(int V);
    ~Graph();
    void addEdge(int v, int w);
    void BFS();    // BFS
    void DFS();    // DFS
};

Graph::Graph(int V) {
    this->V = V;
    adj = new std::list<int> [V];   // init adjacency list
}

Graph::~Graph() {
    delete [] adj;  // need [] attention!
    adj = nullptr;
}

void Graph::addEdge(int v, int w) {
    adj[v].push_back(w);
}

void Graph::BFSUtil(int v, bool* visited) {
    std::queue<int> myqueue;
    visited[v] = true;
    myqueue.push(v);
    while (!myqueue.empty()) {
        v = myqueue.front();
        std::cout << v << " ";
        myqueue.pop();
        for (auto it = adj[v].begin(); it != adj[v].end(); ++it) {
            if (!visited[*it]) {
                visited[*it] = true;
                myqueue.push(*it);
            }
        }
    }
}

void Graph::BFS() {
    bool* visited = new bool[V];
    for (int i = 0; i < V; ++i) {
        visited[i] = false;
    }
    for (int j = 0; j < V; ++j) {
        if (!visited[j]) {
            BFSUtil(j, visited);
        }
    }
}

void Graph::DFSUtil(int v, bool* visited) {
    visited[v] = true;
    std::cout << v << " ";
    for (auto it = adj[v].begin(); it != adj[v].end(); ++it) {
        if (!visited[*it]) {
            DFSUtil(*it, visited);
        }
    }
}

void Graph::DFS() {
    bool* visited = new bool[V];
    for (int i = 0; i < V; ++i) {
        visited[i] = false;
    }
    for (int j = 0; j < V; ++j) {
        if (!visited[j]) {
            DFSUtil(j, visited);
        }
    }
}
int main()
{
    int V(5);
   	Graph g(V);     // create graph
	std::set<int> edgeInput[V];
    edgeInput[0].insert({1, 2});
    edgeInput[1].insert({3, 4});
    for (int i = 0; i < V; ++i) {
        for (auto it = edgeInput[i].begin(); it != edgeInput[i].end(); ++it) {
            g.addEdge(i, *it);     // insert edge
        }
    }
    std::cout << "DFS: " << std::endl;
    g.DFS();
    std::cout << "\nBFS: " << std::endl;
    g.BFS();
    return 0;
}

7. 参考文献

1. 《C++实现数据结构》：图
2. 广度优先搜索的实现
3. 深度优先搜索的实现

这里尤其感谢参考文献2和3，主要也是参考这个代码的，尤其是那种图的数据结构还是比较方便的。