机器学习入门：基于逻辑回归的分类

1、逻辑回归的定义

• 主要解决问题：分类问题—二分类问题

• 如果需要解决多分类问题— softmax 回归

简单来说， 逻辑回归（Logistic Regression）是一种用于解决二分类（0 or 1）问题的机器学习方法，用于估计某种事物的可能性。比如某用户购买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。 注意，这里用的是“可能性”，而非数学上的“概率”，logisitc回归的结果并非数学定义中的概率值，不可以直接当做概率值来用。该结果往往用于和其他特征值加权求和，而非直接相乘。

那么逻辑回归与线性回归是什么关系呢？

逻辑回归（Logistic Regression）与线性回归（Linear Regression）都是一种广义线性模型（generalized linear model）。逻辑回归假设因变量 y 服从伯努利分布，而线性回归假设因变量 y 服从高斯分布。 因此与线性回归有很多相同之处，去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

2、假设函数（Hypothesis function）

与线性回归的区别：线性回归预测输出的是$（-\infty ,+\infty ）$

而逻辑回归输出的是{0,1}，这里面0我们称之为负例，1称之为正例。

如果分类器用的是回归模型，并且已经训练好了一个模型，可以设置一个阈值：

如果$h_{\theta }(x)\ge 0.5，$则预测$y=1$，既$y$属于正例

如果$h_{\theta }(x)<0.5，$则预测$y=0$，既$y$属于负例

对于二分类问题来说，线性回归模型的输出值可以大于1也可以小于0，所以我们需要一个函数，将输出转换到0和1之间。这里我们引入一个函数，Sigmoid函数。

首先我们要先介绍一下Sigmoid函数，也称为逻辑函数（Logistic function）：
’

$g(z)=\frac{1}{1+e^{-z}}$
其函数曲线如下：

从上图可以看到sigmoid函数是一个s形的曲线，它的取值在[0, 1]之间，在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要

逻辑回归的假设函数形式如下：
$$h_{\theta }(x)=g({\theta }^{T}x),g(z)=\frac{1}{1+e^{-z}}$$
所以：
$$h_{\theta }(x)=\frac{1}{1+e^{-({\theta }^{T}x)}}$$

其中 $x$ 是我们的输入， $\theta$ 为我们要求取的参数。

上面式子也可变化为：
’

$\ln \frac{h_{\theta }(x)}{1-h_{\theta }(x)}={\theta }^{T}x$
如果 $h_{\theta }(x)$是样本 $x$正例的概率，所以 $1-h_{\theta }(x)$是取反例的可能性，两者比值 $\frac{h_{\theta }(x)}{1-h_{\theta }(x)}$ 称为“几率”（odds），反应了正例的可能性。几率取对数则得到”对数几率“（log odds，亦称logit）
’ $\ln \frac{h_{\theta }(x)}{1-h_{\theta }(x)}$

我们可以看出上面公式实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率。因此，其对应的模型称为"对数几率回归" 或者”逻辑回归“(logistic regression，亦称logit regression) 。特别需注意到，虽然它的名字是"回归"，但实际却是一种分类学习方法。

3、损失函数（Cost Function）

如何确定$\theta$ , 我们常用的损失函数有均方误差和交叉熵。对于逻辑回归我们选择交叉熵作为损失函数。

给定输入$x$，参数化$\theta$，$y=1$和$y=0$时的概率，数学表达为：
$$\begin{gathered} P(y=1|x;\theta )=h_{\theta }(x) \\ P(y=0|x;\theta )=1-h_{\theta }(x) \end{gathered}$$
所以
$$P(y|x;\theta )=(h_{\theta }(x){)}^y(1-h_{\theta }(x){)}^{1-y}$$
对应的似然函数为：
$$L(\theta )=\prod _{i=1}^{m}P(y^{(i)};\theta )=\prod _{i=1}^m(h_{\theta }(x^{(i)}){)}^{y^{(i)}}(1-h_{\theta }(x^{(i)}){)}^{1-y^{(i)}}$$
给定数据集$\{(x_i,y_i){\}}_{i=1}^m$，逻辑回归模型最大化对数似然函数来估计$\theta$
$$l(\theta )=\log L(\theta )=\sum _{i=1}^m{y}^{(i)}\log (h_{\theta }(x^{(i)}))+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))$$

对数似然取最大值等价于损失函数交叉熵取最小值

4、代码实现

4.1 先尝试调用sklearn的线性回归模型训练数据，尝试以下代码，画图查看分类的结果

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

df_X = pd.read_csv('./logistic_x.txt', sep='\ +',header=None, engine='python') #读取X值
ys = pd.read_csv('./logistic_y.txt', sep='\ +',header=None, engine='python') #读取y值
ys = ys.astype(int)
df_X['label'] = ys[0].values #将X按照y值的结果一一打标签

ax = plt.axes()
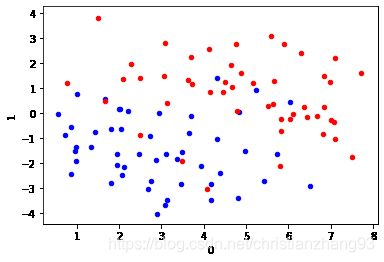
#在二维图中描绘X点所处位置，直观查看数据点的分布情况
df_X.query('label == 0').plot.scatter(x=0, y=1, ax=ax, color='blue')
df_X.query('label == 1').plot.scatter(x=0, y=1, ax=ax, color='red')

#提取用于学习的数据
Xs = df_X[[0, 1]].values
Xs = np.hstack([np.ones((Xs.shape[0], 1)), Xs]) 
ys = df_X['label'].values

from __future__ import print_function
import numpy as np
from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(fit_intercept=False) #因为前面已经将截距项的值合并到变量中，此处参数设置不需要截距项
lr.fit(Xs, ys) #拟合
score = lr.score(Xs, ys) #结果评价
print("Coefficient: %s" % lr.coef_)
print("Score: %s" % score)

Coefficient: [[-1.70090714  0.55446484  1.07222372]]
Score: 0.898989898989899


/home/xiaoran/anaconda3/lib/python3.6/site-packages/sklearn/linear_model/logistic.py:432: FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
  FutureWarning)

ax = plt.axes()

df_X.query('label == 0').plot.scatter(x=0, y=1, ax=ax, color='blue')
df_X.query('label == 1').plot.scatter(x=0, y=1, ax=ax, color='red')

_xs = np.array([np.min(Xs[:,1]), np.max(Xs[:,1])])

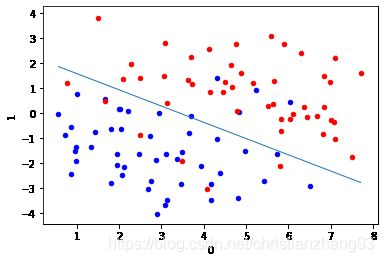
#将数据以二维图形式描点，并用学习得出的参数结果作为阈值，划分数据区域
_ys = (lr.coef_[0][0] + lr.coef_[0][1] * _xs) / (- lr.coef_[0][2])
plt.plot(_xs, _ys, lw=1)

[]

4.2 用梯度下降法将相同的数据分类，画图和sklearn的结果相比较

class LGR_GD():
    def __init__(self):
        self.w = None 
        self.n_iters = None
    def fit(self,X,y,alpha=0.03,loss = 1e-10): # 设定步长为0.002，判断是否收敛的条件为1e-10
        y = y.reshape(-1,1) #重塑y值的维度以便矩阵运算
        [m,d] = np.shape(X) #自变量的维度
        self.w = np.zeros((1,d)) #将参数的初始值定为0
        tol = 1e5
        self.n_iters = 0
        #============================= show me your code =======================
        while tol > loss: #设置收敛条件
            
            self.n_iters += 1 #更新迭代次数
         #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        y_pred = X.dot(self.w)
        return y_pred  

if __name__ == "__main__":
    lr_gd = LGR_GD()
    lr_gd.fit(Xs,ys)

    ax = plt.axes()

    df_X.query('label == 0').plot.scatter(x=0, y=1, ax=ax, color='blue')
    df_X.query('label == 1').plot.scatter(x=0, y=1, ax=ax, color='red')

    _xs = np.array([np.min(Xs[:,1]), np.max(Xs[:,1])])
    _ys = (lr_gd.w[0][0] + lr_gd.w[0][1] * _xs) / (- lr_gd.w[0][2])
    plt.plot(_xs, _ys, lw=1)

4.3 用牛顿法实现结果，画图和sklearn的结果相比较，并比较牛顿法和梯度下降法迭代收敛的次数

class LGR_NT():
    def __init__(self):
        self.w = None
        self.n_iters = None
    def fit(self,X,y,loss = 1e-10): # 判断是否收敛的条件为1e-10
        y = y.reshape(-1,1) #重塑y值的维度以便矩阵运算
        [m,d] = np.shape(X) #自变量的维度
        self.w = np.zeros((1,d)) #将参数的初始值定为0
        tol = 1e5
        n_iters =0
        Hessian = np.zeros((d,d))
        #============================= show me your code =======================
        while tol > loss:
            
            n_iters += 1
        #============================= show me your code =======================
        self.w = theta
        self.n_iters = n_iters
        
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        y_pred = X.dot(self.w)
        return y_pred  

if __name__ == "__main__":
    lgr_nt = LGR_NT()
    lgr_nt.fit(Xs,ys)

4.4 比较梯度下降法和牛顿法收敛速度

print("梯度下降法结果参数：%s;梯度下降法迭代次数：%s" %(lgr_gd.w,lgr_gd.n_iters))
print("牛顿法结果参数：%s;牛顿法迭代次数：%s" %(lgr_nt.w,lgr_nt.n_iters))

梯度下降法结果参数：[[-2.62051144  0.7603715   1.17194673]];梯度下降法迭代次数：32590
牛顿法结果参数：[[-2.6205116   0.76037154  1.17194674]];牛顿法迭代次数：47

可以，看到，牛顿法的收敛速度比梯度下降法快很多。