如何搭建LSTM(pytorch版)
一 、单向LSTM
0.导入包
import torch
1.rnn = torch.nn.LSTM(input_size,hidden_size,num_layers)
rnn = torch.nn.LSTM(10, 20, 2) #(input_size,hidden_size,num_layers)
括号里面第一个参数input_size是输入向量的维度,第二个参数hidden_size是隐藏层向量的维度,第三个参数num_layers代表循环层的数量。
第三个参数num_layers不太好理解,可以通过下图理解一下:

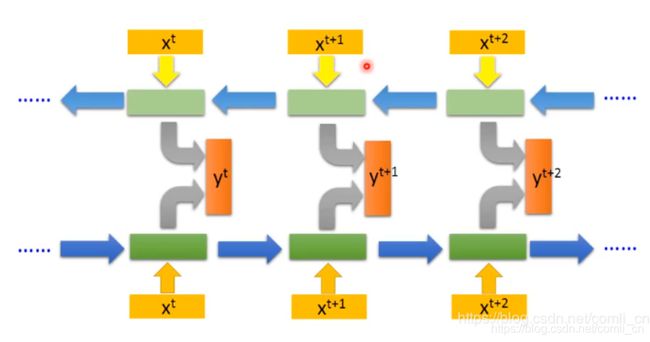
一般num_layers默认为1,当num_layers为2时就是上图画的这样了,将第一层输出的h_t作为第二层的输入,这是在空间上展开的样子,而我们经常能看到的是在时间上展开的样子,如下图(num_layers=1时在时间轴上展开的样子):
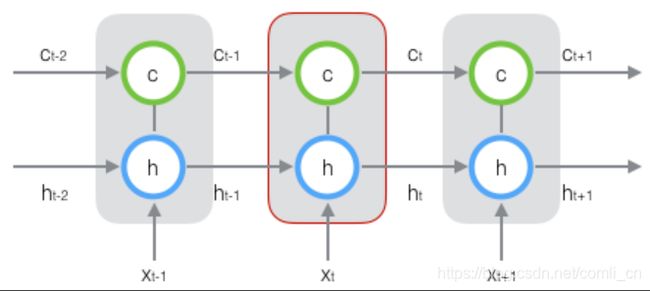
因此我们对LSTM应用反向传播算法时既要计算误差沿时间的传播又要计算误差沿层的传播,而普通的全连接神经网络在做反向传播时只需要计算误差沿层的传播即可,如下图
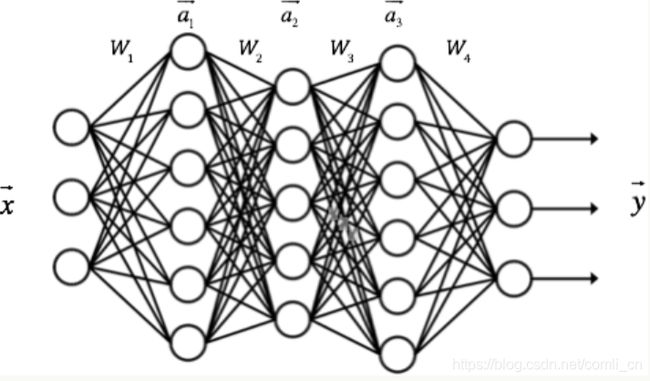
所以可以将LSTM与全连接神经网络做个类比:
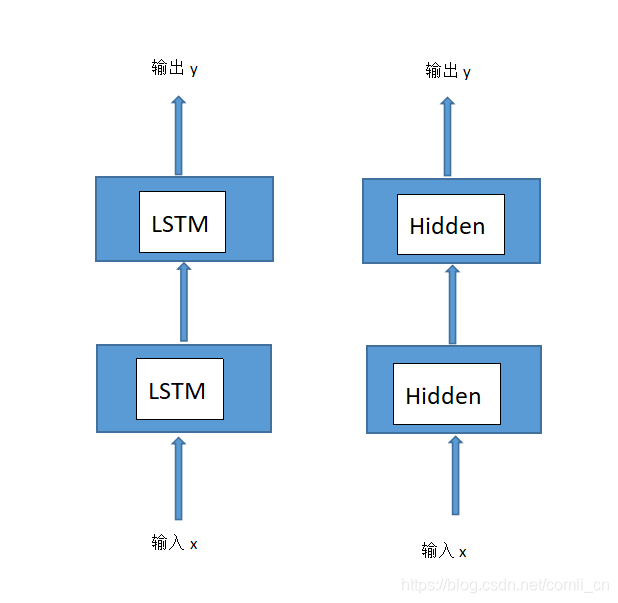 我们去掉具体的一根根连线可以看到LSTM与全连接神经网络是十分类似的,LSTM只是对普通的隐藏层进行了功能拓展。
我们去掉具体的一根根连线可以看到LSTM与全连接神经网络是十分类似的,LSTM只是对普通的隐藏层进行了功能拓展。
2.input = torch.randn(seq_len, batch, input_size)
input = torch.randn(5, 3, 10)#(seq_len, batch, input_size)
生成一个形状 5 ∗ 3 ∗ 10 5*3*10 5∗3∗10的张量,张量里面的元素是服从标准正态分布的随机数。
张量的通俗理解见链接: link.
第二个参数batch表示将整个输入序列分成了3个小batch(即进行批量化),第一个参数seq_len表示每个小batch需要几个时间步进行处理,第三个参数input_size是输入向量的维度。
batch参考.
这里为什么要就行批量化呢,是为了在使用梯度下降的时候方便一些,既不用每处理一个输入的最小单元就更新参数,也不用等全部输入处理完再更新所有参数。这里可以参考一下小批量梯度下降。
3.两个初始化
h0 = torch.randn(2, 3, 20) #(num_layers,batch,output_size)
c0 = torch.randn(2, 3, 20) #(num_layers,batch,output_size)
4.前向计算
output, (hn, cn) = rnn(input, (h0, c0))
将输入input,和初始的h0,c0放到rnn中就会进行前向计算,算出输出output和hn, cn,当然这里的rnn已经是被实例化的LSTM(见第一个标题)。
二 、双向LSTM
import torch
rnn = torch.nn.LSTM(input_size=10, hidden_size=20, num_layers=2,bidirectional=True)#(input_size,hidden_size,num_layers)
input = torch.randn(5, 3, 10)#(seq_len, batch, input_size)
h0 = torch.randn(4, 3, 20) #(num_layers,batch,output_size)
c0 = torch.randn(4, 3, 20) #(num_layers,batch,output_size)
output, (hn, cn) = rnn(input, (h0, c0))
只要在torch.nn.LSTM()的括号中加入bidirectional=True就开启了双向LSTM。双向LSTM与单向LSTM的区别在于单向LSTM在计算一个时间步的相关数值时只可以用到前面几步的数值,而双向LSTM既能用到前面几步的数值又能用到后面几步的数值。
比如说在补充一句话的时候:
“我要去__。”
这时用单向LSTM可以推测出空格里面应该填一个地名。但如果残句变为:
“我要__学校。”
这是只根据“我要”这两个字很难推出空格里面内容,但是如果结合“学校”就可以准确推测了。这就是双向LSTM的应用场景了。