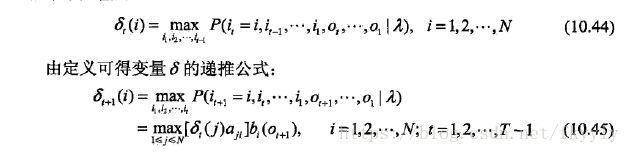HMM,MEMM,CRF总结和比较
HMM(隐马尔科夫)
![]()
1 HMM是产生式模型
HMM是一种产生式模型,定义了联合概率分布p(x,y) ,其中x和y分别表示观察序列和相对应的标注序列的随机变量。为了能够定义这种联合概率分布,产生式模型需要枚举出所有可能的观察序列,这在实际运算过程中很困难,所以我们可以将观察序列的元素看做是彼此孤立的个体, 即假设每个元素彼此独立(和naive bayes类似),任何时刻的观察结果只依赖于该时刻的状态。
2 特点(两个基本假设):
(1)后一个隐藏状态只依赖于前一个隐藏状态。
或者可以称为马尔科夫假设(Markov Assumption)或者一阶马尔科夫链:下一个词的出现仅依赖于它前面的一个或几个词。
(2)观测值之间相互独立,观测值只依赖于该时刻的马尔科夫链的隐状态。
3 两个状态集合
(1)隐藏状态集合(假如是N*1维),例如是分词任务的词性
(2)观测状态集合(假如是M*1维),例如是分词任务具体的一个单词
4 模型的元素
(1)初始概率向量PI,是指隐藏状态集合的初始分布(N维)
(2)状态转移概率矩阵A,是指任意两个隐藏状态之间的转变概率(N*N维)
(3)观测概率矩阵(或者称为混淆矩阵)B,是指隐藏状态到观测状态的变化矩阵(N*M维)
5 三个基本问题
(1)评估问题(概率计算),已知模型参数 λ= (A, B, π)和观测序列O,求在该模型λ下求观测序列O出现的概率P(O|λ)
(2)学习问题(训练),已知观测序列O,求模型参数 λ=(π, A, B), 使得P(O|λ)最大。
(3)解码问题(预测),已知观测序列O和模型参数参数 λ=(π, A, B),求一个隐藏状态序列S(s1,s2,...st),能最好的解释观测序列O(o1,o2,...ot)。也就是输出最可能的隐藏序列S(s1,s2,...st)。
上面训练的时候没有涉及到隐状态,所以用HMM是通过求联合概率P(x,y),在通过贝叶斯公式求得P(y|x)的。
所以HMM是生成模型。
6 对于上面第一种问题:评估问题(概率计算)解决方案
(1)直接计算(实际不可行)
对于输入的观测序列O(o1,o2...ot),通过列举所有可能长度为t的隐藏状态序列S(s1,s2,...st)。求所有可能的状态序列的和即可求得P(O|λ)。
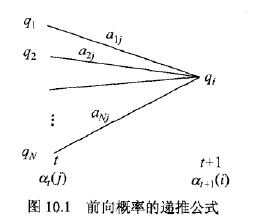
(2)前向算法 (前向递推)
需要定义一个辅助量称为前向概率(名字无所谓)表示到时刻t部分观测序列(o1,o2...,ot)且此时隐状态为qi的概率。
其实核心就是要考虑到状态集合和观测序列集合的信息。
其中第二步递推公式的由来按照如下图来理解,此时是时刻t+1,此时的状态是qi。前一时刻t,各种状态都有可能q1q2...qN
(3)后向算法 (后向递推)
就是和前向算法不同之处是:定义的辅助变量是t时刻之后的观察序列,计算递推公式的方向相反
7 对于上面第二种问题:学习问题(训练)解决方案,就是学习模型参数
依赖于数据源分两种情况。如果训练数据是包含观测序列和隐藏状态序列的就可以用监督学习,如果只有观测序列那么久无监督学习。
7.1 有监督:极大似然,其实就是先验统计
训练语料是n个长度相同的观测序列和对应的隐藏状态序列{(O1,S1),(O2,S2)...(On,Sn)}
(1)初始概率向量PI(N维)
训练样本中隐藏状态的先验概率(直接统计)
(2)状态转移概率矩阵A(N*N维)
(直接统计)
(3)观测概率矩阵(或者称为混淆矩阵)B(N*M维)
(直接统计)
7.2 无监督:Baum-Welch算法也就是EM算法
8 对于上面第三种问题:解码问题(预测)【已知模型参数和观测序列,求隐藏序列】
主要有如下两种方法
8.1 近似算法
每个时刻选择在该时刻最有可能出现的状态,该方法是贪心的保证每个时刻的最优状态,没有考虑时序关系,不保证全局最优。
8.2 维特比算法(动态规划算法)
用动态规划来求概率最大的路径即最优路径。动态规划两个要素最优子结构和重叠子问题。
最优子结构:如果问题的一个最优解包含了子问题的最优解,则该问题具有最优子结构。当一个问题具有最优子结构的时候,我们就可能要用到动态规划(贪心策略也是有可能适用的)。
重叠子问题:适用于动态规划求解的最优化问题必须具有的第二个要素是子问题的空间要“很小”,也就是用来解原问题的递归算法可以反复的解同样的子问题,而不是总在产生新的子问题。典型的,当一个递归算法不断的调用同一问题时,我们说该最优问题包含重叠子问题。
求解:
需要引入辅助变量δ和φ。δ时刻t隐藏状态为i的所有单个路径(i1,i2,...,it)中概率最大的路径。
φ表示时刻t状态为i的所有单个路径(i1,i2,...,it)中概率最大路径的第t-1时刻节点的隐状态
具体求解过程