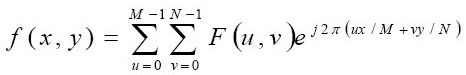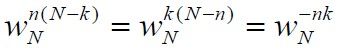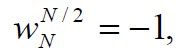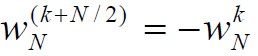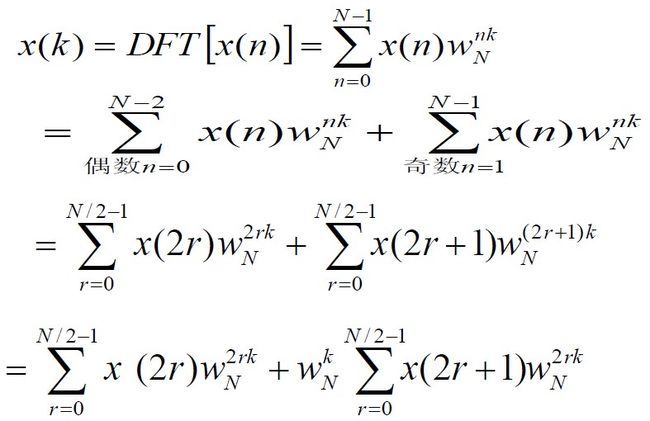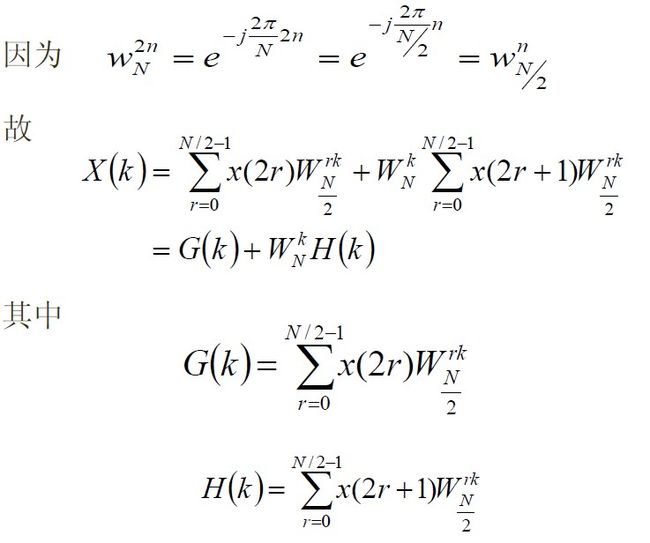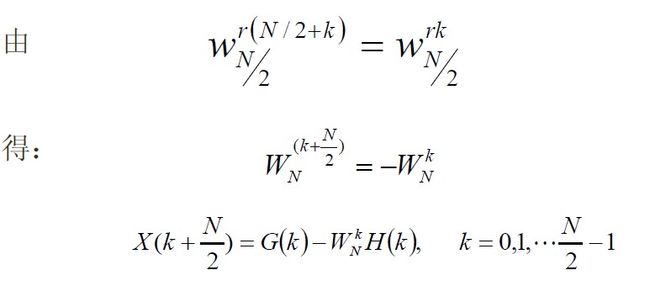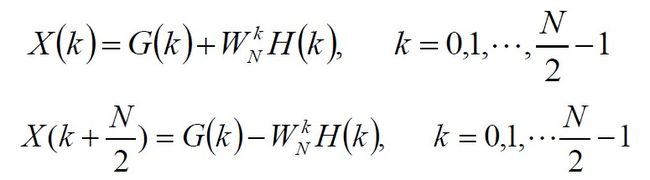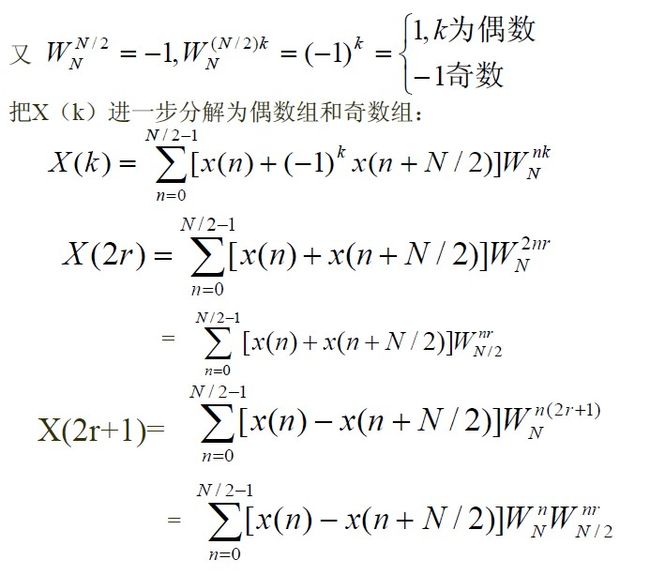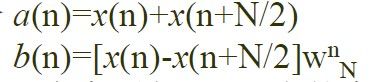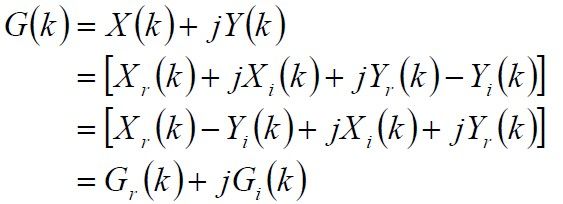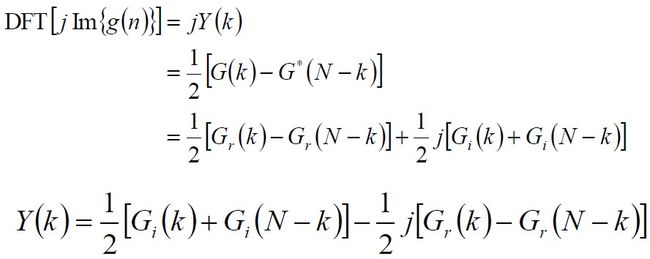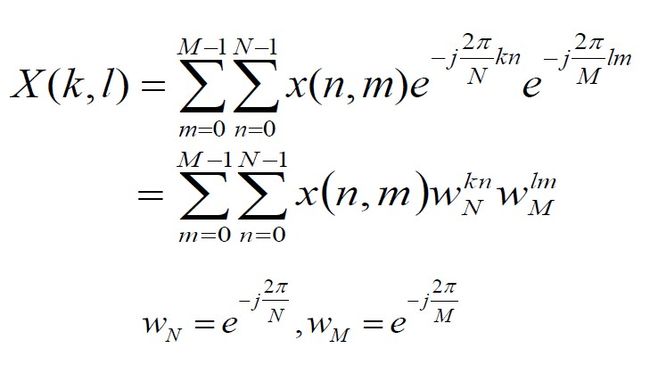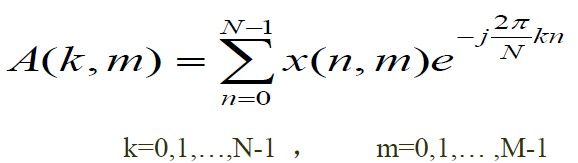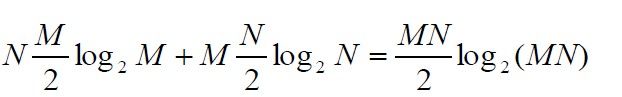图像的时频变换——离散傅里叶变换
一直很纳闷,几乎所有数字图像处理的书都会介绍数字时频变换,但是却很少书会讲时频变换的作用,这也是让我一直很疑惑的地方(不过也极有可能是本人愚钝)。频谱技术通常用于提高图像的处理操作速率,频谱相当于是图像的特征,时频变换虽然是一种数学技巧,但是运用到数字图像处理上会方便和简单。研究的图像变换基本上都是正交变换,正交变换可以减少图像数据的相关性,获取图像的整体特点,有利于用较少的数据量表示原始图像,这对图像的分析、存储以及图像的传输都是非常有意义的。这里介绍了离散傅立叶变换、离散余弦变换、沃尔什-哈达玛变换及小波变换的基本理论和知识并进行图像时频变换实验。
一、二维离散傅里叶变换
一个图像尺寸为M×N的 函数f(x,y)的离散傅里叶变换由以下等式给出:
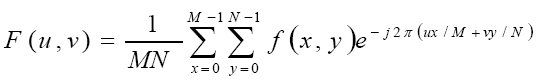
其中 u=0,1,2,...,M-1和v=0,1,2,...,N-1。其中变量u和v用于确定它们的频率,频域系统是由F(u,v)所张成的坐标系,其中u和v用做(频率)变量。空间域是由f(x,y)所张成的坐标系。可以得到频谱系统在频谱图四角(0,0),(0,N-1),(N-1,0),(N-1,N-1)处沿u和v方向的频谱分量均为0。
离散傅里叶逆变换由下式给出:
令R和I分别表示F的实部和需部,则傅里叶频谱,相位角,功率谱(幅度)定义如下:
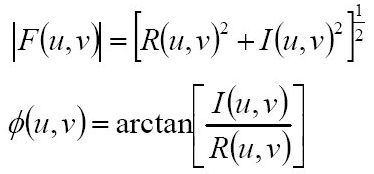
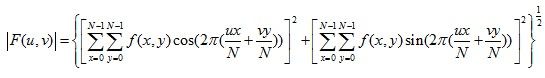
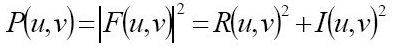
在频谱的原点变换值称为傅里叶变换的直流分量,下面是傅里叶变换的周期公式:
![]()
![]()
DFT实现仅计算一个周期,所以可以处理M X N的数组,由周期性可知,A,B,C,D是四个分别的四分之一周期。

图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。变换最慢的频率成分(u=v=0)对应一幅图像的平均灰度级。当从变换的原点移开时,低频对应着图像的慢变换分量,较高的频率开始对应图像中变化越来越快的灰度级。这些事物体的边缘和由灰度级的突发改变(如噪声)标志的图像成分。通常在进行傅里叶变换之前用(-1)^(x+y)乘以输入的图像函数,这样就可以将傅里叶变换的原点F(0,0)移到(M/2,N/2)上。
二、算法原理
离散快速傅里叶变换(FFT)是在离散傅立叶变换(DFT)的基础上改进的,为了更好的理解FFT算法,先对DFT进行梳理下,
1、DFT运算的特点:
首先分析有限长序列x(n)进行一次DFT运算所需的运算量。
一般,x(n)和![]() 都是复数,因此,每计算一个X(k)值,要进行N次复数相乘,和N-1次复数相加,X(k)一共有N个点,故完成全部DFT运算,需要N^2次复数相乘和N(N-1)次复数相加,在这些运算中,乘法比加法复杂,需要的运算时间多,尤其是复数相乘,每个复数相乘包括4个实数相乘和2个实数相加,例
都是复数,因此,每计算一个X(k)值,要进行N次复数相乘,和N-1次复数相加,X(k)一共有N个点,故完成全部DFT运算,需要N^2次复数相乘和N(N-1)次复数相加,在这些运算中,乘法比加法复杂,需要的运算时间多,尤其是复数相乘,每个复数相乘包括4个实数相乘和2个实数相加,例
又每个复数相加包括2个实数相加,所以,每计算一个X(k)要进行4^N次实数相乘和2N+2(N-1)=2(2N-1)次实数相加,因此,整个DFT运算需要4N^2实数相乘和2N(2N-1)次实数相加。
2、FFT算法的基本思想:
考察DFT与IDFT的运算发现,利用以下两个特性可减少运算量:
1)系数 是一个周期函数,它的周期性和对称性可用来改进运算,提高计算效率。
是一个周期函数,它的周期性和对称性可用来改进运算,提高计算效率。
利用这些周期性和对称性,使DFT运算中有些项可合并;
2)利用的![]() 周期性和对称性,把长度为N点的大点数的DFT运算依次分解为若干个小点数的DFT。因为DFT的计算量正比于N二次方,N小,计算量也就小。
周期性和对称性,把长度为N点的大点数的DFT运算依次分解为若干个小点数的DFT。因为DFT的计算量正比于N二次方,N小,计算量也就小。
FFT算法正是基于这样的基本思想发展起来的。它有多种形式,但基本上可分为两类:时间抽取法和频率抽取法。
3、按时间抽取的FFT(N点DFT运算的分解)
假设采样序列点数为N=2^L,L为整数,如果不满足这个条件可以人为地添加若干个0以使采样序列点数满足这一要求。首先我们将序列x(n)按照奇偶分为两组如下:
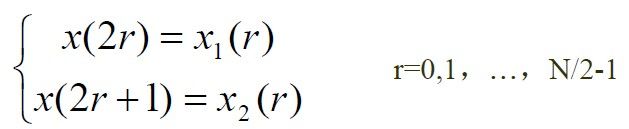
注意到,H(k),G(k)有N/2个点,即k=0,1,…,N/2-1,还必须应用系数![]() 的周期性和对称性表示X(k)的N/2 ~N-1点:
的周期性和对称性表示X(k)的N/2 ~N-1点:
可见,一个N点的DFT被分解为两个N/2点的DFT,这两个N/2点的DFT再合成为一个N点DFT
依此类推,G(k)和H(k)可以继续分下去,这种按时间抽取算法是在输入序列分成越来越小的子序列上执行DFT运算,最后再合成为N点的DFT。
蝶形信号流图
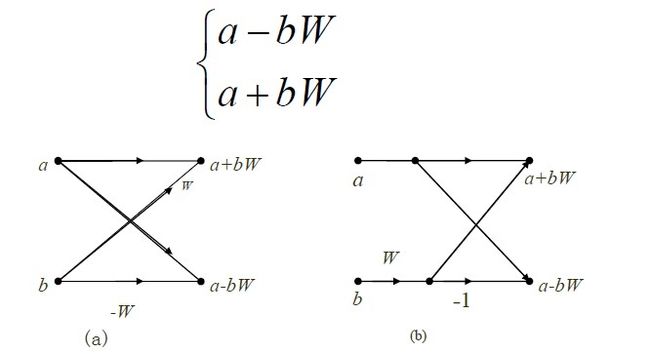
将G(k)和H(k) 合成X(k)运算可归结为:
蝶形运算的简化
图(a)为实现这一运算的一般方法,它需要两次乘法、两次加减法。考虑到-bW和bW两个乘法仅相差一负号,可将图(a)简化成图2.7(b),此时仅需一次乘法、两次加减法。图(b)的运算结构像一蝴蝶通常称作蝶形运算结构简称蝶形结,采用这种表示法,就可以将以上所讨论的分解过程用流图表示。
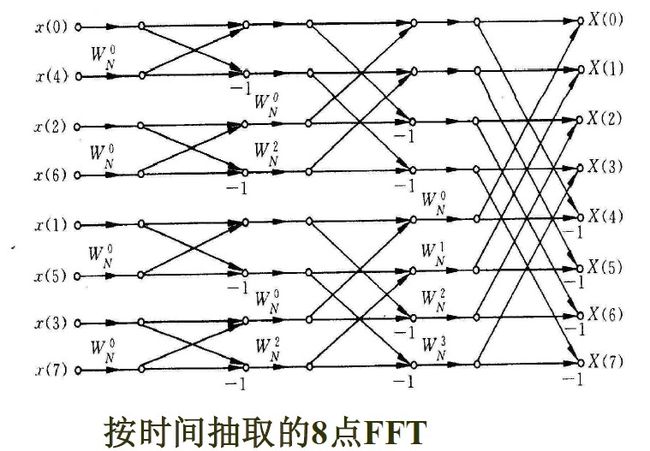
N=2^3=8的例子。

按照这个办法,继续把N/2用2除,由于N=2M,仍然是偶数,可以被2整除,因此可以对两个N/2点的DFT再分别作进一步的分解。即对{G(k)}和{H(k)}的计算,又可以分别通过计算两个长度为N/4=2点的DFT,进一步节省计算量,见图。这样,一个8点的DFT就可以分解为四个2点的DFT。
这样,一个8点的完整的按时间抽取运算的流图
由于这种方法每一步分解都是按输入时间序列是属于偶数还是奇数来抽取的,所以称为“按时间抽取法”或“时间抽取法”。
4、按频率抽取的FFT(按输出X(k)在频域的顺序上属于偶数还是奇数分解为两组)
对于N=2^M情况下的另外一种普遍使用的FFT结构是频率抽取法。
对于频率抽取法,输入序列不是按偶数奇数,而是按前后对半分开,这样便将N点DFT写成前后两部分:
这两个序列都是N/2点的序列,将其代入上两式,得

这正是两个N/2点的DFT运算,即将一个N点的DFT分解为两个N/2点的DFT,上式的运算关系可用下图表示.
以N=8的频率抽取为例
与时间抽取法一样,由于N=2M,N/2仍是一个偶数,这样,一个N=2M点的DFT通过M次分解后,最后只剩下全部是2点的DFT,2点DFT实际上只有加减运算。但为了比较,也为了统一运算的结构,仍用一个系数为W0N的蝶形运算来表示。
频率抽取法的流图是时域抽取法流图的左右翻转。下图是N=8的频率抽取法FFT流图。
N=8的按频率抽取FFT运算流图
5、实数序列的FFT
以上讨论的FFT算法都是复数运算,包括序列x(n)也认为是复数,但大多数场合,信号是实数序列,任何实数都可看成虚部为零的复数,例如,求某实信号x(n)的复谱,可认为是将实信号加上数值为零的虚部变成复信号(x(n)+j0),再用FFT求其离散傅里叶变换。这种作法很不经济,因为把实序列变成复序列,存储器要增加一倍,且计算机运行时,即使虚部为零,也要进行涉及虚部的运算,浪费了运算量。合理的解决方法是利用复数据FFT对实数据进行有效计算,下面介绍两种方法。
(1)用一个N点FFT同时计算两个N点实序列的DFT设x(n)、y(n)是彼此独立的两个N点实序列,且X(k)=DFT[x(n)],Y(k)=DFT[y(n)],则X(k)、Y(k)可通过一次FFT运算同时获得。
首先将x(n)、y(n)分别当作一复序列的实部及虚部,令g(n)=x(n)+jy(n)
通过FFT运算可获得g(n)的DFT值
利用离散傅里叶变换的共轭对称性
通过g(n)的FFT运算结果G(k),由上式可得到X(k)的值。
通过g(n)的FFT运算结果G(k),由上式也可得
到Y (k) 的值。
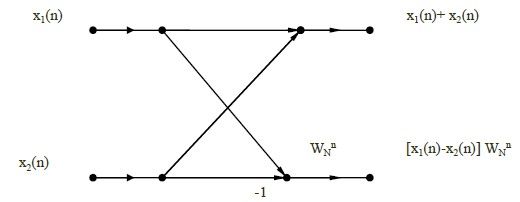
作一次N点复序列的FFT,再通过加、减法运算就可以
将X(k)与Y(k)分离出来。显然,这将使运算效率提高一倍。
6、用FFT计算二维离散的傅里叶变换
前面介绍的FFT原理都是关于一维傅里叶变换的,终于又能切回正题了,数字图像傅里叶变换明显是一个二维的离散傅里叶变换,二维信号有图象信号、时空信号、时频信号等。二维离散傅里叶变换可用于处理二维离散信号。
二维离散傅里叶变换的定义为:
二维离散傅里叶变换可通过两次一维离散傅里叶变换来实现:
1)作一维N点DFT(对每个m做一次,共M次)
2)作M点的DFT(对每个k做一次,共N次)
这两次离散傅里叶变换都可以用快速算法求得,若M和N都是2的幂,则可使用基二FFT算法,所需要乘法次数为
而直接计算二维离散傅里叶变换所需的乘法次数为(M+N)MN,当M和N比较大时用用FFT运算,可节约很多运算量。
三、基于数字图像处理FFT编程实现
数字图像处理的快速傅里叶变换操作一共有下面3步
1)获取图片的像素的灰度数组
double[] iPix = new double[iw * ih];//输入灰度
pixels = common.grabber(iImage, iw, ih); //获得像素数组
for (int i = 0; i < iw*ih; i++) //获得像素灰度值
iPix[i] = pixels[i]&0xff;
2)对灰度数组进行傅里叶变换
//FFT变换
FFT2 fft2 = new FFT2();
fft2.setData2(iw, ih, iPix);
fftData = fft2.getFFT2();
第二层循环:由于第L级有2^(L-1)个蝶形因子(乘数),第二层循环根据乘数进行控制,保证对于每一个蝶形因子第三层循环要执行一次,这样,第三层循环在第二层循环控制下,每一级要进行2^(L-1)次循环计算。(L=1,2.......m)
第三层循环:由于第L级共有N/2^L个群,并且同一级内不同群的乘数分布相同,当第二层循环确定某一乘数后,第三层循环要将本级中每个群中具有这一乘数的蝶形计算一次,即第三层循环每执行完一次要进行N/2^L个碟形计算。
可以得出结论:在每一级中,第三层循环完成N/2^L个碟形计算;第二层循环使第三层循环进行 2^(L-1)次,因此,第二层循环完成时,共进行2^(L-1) *N/2^L=N/2个碟形计算。实质是:第二、第三层循环完成了第L级的计算。
几个要注意的数据:
① 在第L级中,每个碟形的两个输入端相距b=2^(L-1)个点(程序中的bfsize/2)。
② 同一乘数对应着相邻间隔为2^L=2*b个点的N/2^L个碟形。
③ 第L级的2^(L-1)个碟形因子W N[p]中的P,可表示为p = j*2^(m-L),
其中j = 0,1,2,...,2^(L-1)-1
private Complex[] getData1()
{
//蝶形运算
for (k = 0; k < power; k++)
{
for (j = 0; j < 1 << k; j++)
{
bfsize = 1 << (power - k);
for (i = 0; i < bfsize / 2; i++)
{
Complex temp1 = new Complex(0, 0);
Complex temp2 = new Complex(0, 0);
p = j * bfsize;
x2[i + p] = temp1.Add(x1[i + p], x1[i + p + bfsize / 2]);
temp2 = temp1.Sub(x1[i + p], x1[i + p + bfsize / 2]);
x2[i + p + bfsize / 2] = temp1.Mul(temp2, wc[i * (1 << k)]);
}
}
x = x1;
x1 = x2;
x2 = x;
}
//重新排序
for (j = 0; j < count; j++)
{
p = 0;
for (i = 0; i < power; i++)
if ((j & (1 << i)) != 0)
p += 1 << (power - i - 1);
fd1[j] = x1[p];
}
return fd1;
}
3)FFT数据的可视化
使用傅里叶频谱来可视化FFT变换得到的数据
//FFT数据可视化
public int[] toPix(Complex[] fftData, int iw, int ih)
{
int[] pix = new int[iw*ih];
int u, v, r;
for (int j = 0; j < ih; j++)
{
for (int i = 0; i < iw; i++)
{
double tem = fftData[i + j * iw].re * fftData[i + j * iw].re
+ fftData[i + j * iw].im * fftData[i + j * iw].im;
r = (int)(Math.sqrt(tem) / 100);
if (r > 255) r = 255;
//移到中心
if (i < iw / 2) u = i + iw / 2;
else u = i - iw / 2;
if (j < ih / 2) v = j + ih / 2;
else v = j - ih / 2;
pix[i + j * iw] = 255 << 24|r << 16|r << 8|r;
}
}
return pix;
} 实验效果如下: