如何操作网络数据?(三)
R语言社交网络快速入门(一)(7天入门社交网络)
R语言社交网络快速入门(二)(7天入门社交网络)
R语言社交网络快速入门(三)(7天入门社交网络)
R语言社交网络快速入门(四)(7天入门社交网络)
R语言社交网络快速入门(五)(7天入门社交网络)
网络数据操作
简介
简单来说,网络指的就是一组元素及其相互关系。图论为这一概念进行了铺垫。我们将介绍图形的基本元素、无向图和定向图,以及如何生成网络图,包括手动输入和从各种网络数据导入。
作为一个复杂系统的表示,一个简单的图形通常是不够的。相反,额外的信息对应用程序非常重要,比如可以通过顶点(比如社交网络成员的性别)或者边缘(比如在运输网络中遍历路径所需的时间)索引的变量形式。
最后,在使用图形表示网络数据时,需要先熟悉一些图论的基本概念以及评估图形基本属性的能力。因此,我们会快速地介绍这些基本概念。
为了创建、修饰和评估网络图的基本属性,我向你强烈推荐igraph。igraph是一个用于网络分析的库和r包,它自带了一系列数据和函数用来直接创建网络图和图形算法的快速实现。快速处理大型图(数百万个顶点和边)。
这是我买的介绍igraph的书:

你也可以在他的官网查看相关内容(http://igraph.org/)
创建第一张网络图
无向图和有向图
在形式上,图G(V,E)是一个数学结构,由一组顶点的集合V(通常被称为节点)和一组边(通常称为链路)组成,其中E的元素是无序对{u,v},它们分别为
典型的图
双列列表
A->B A->C B->C C->B
稀疏矩阵形式
7 x 7 sparse Matrix of class “dgCMatrix”
1 2 3 4 5 6 7
1 . 1 1 … .
2 1 . 1 1 …
3 1 1 . . 1 . .
4 . 1 . . 1 1 1
5 . . 1 1 . 1 .
6 … 1 1 . 1
7 … 1 . 1 .
修饰网络图
顶点、边缘和图属性
顶点名称赋值
V(dg) name<−c(‘A′,′B′,′C′)V(dg) n a m e < − c ( ‘ A ′ , ′ B ′ , ′ C ′ ) V ( d g ) gender <- c(‘M’,’F’,’M’)
V(g)$color <- ‘red’
边赋值权重
wg <- g
E(wg)$weight <- runif(ecount(wg))
图的名字
g$name <- ‘XuHousheng’
导入数据
library(igraphdata)
library(sand)
g.lazega <- graph.data.frame(elist.lazega,
directed = ‘FALSE’,
vertices = v.attr.lazega)
plot(g.lazega)

基础图和特别的图
通过采用基于图形的框架来表示网络分析中的关系数据,我们用具体的名词来讨论与图形相关的各种重要规则。我们简单介绍了一些,这是做网络分析的基础。
如果一个图中有循环边或者多边的顶点对,那么我称它叫复合图(其实就是复杂图的意思-。-),反之,则称为简单图。
我们的第一张图就是简单图,下面是一张复合图的例子。
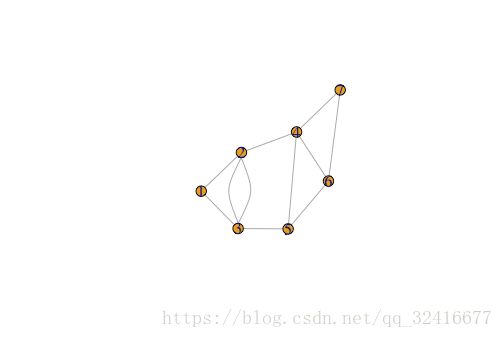
检查一张图是否是简单图看似是一件小事,但却是非常重要的。因为许多模型和算法的前提假设图是简单图,如果不是,就得不出正确的结果。
连通性:
无向图只要没有孤立的顶点即是连通图
无向图分为弱连通图和强连通图,我们之前提到就是弱连通图。强连通图要求两两顶点互连。
网络图的距离:
在图上顶点之间的距离通常定义为顶点之间最短路径的长度(如果没有,则称为无穷大)。这个距离通常被称为测地距离,测地线是最短路径的简称。图中最长的路径称为图的直径。
特殊图:
图的形状大小都是一样的,但在实践中需要选择特定的图形种类。
比如:
铺满
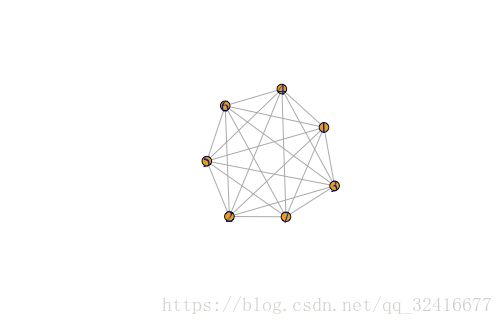
环形

树状
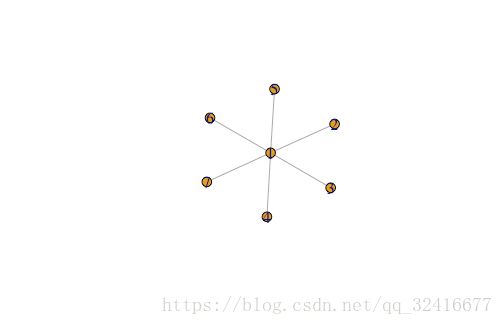
星状
有向无环图:
有向无环图指的是一个无回路的有向图。有向无环图是描述一项工程或系统的进行过程的有效工具。
二部图:
简而言之,就是顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
如下图所示




