隐马尔可夫模型（三）——隐马尔可夫模型的评估问题(前向算法）

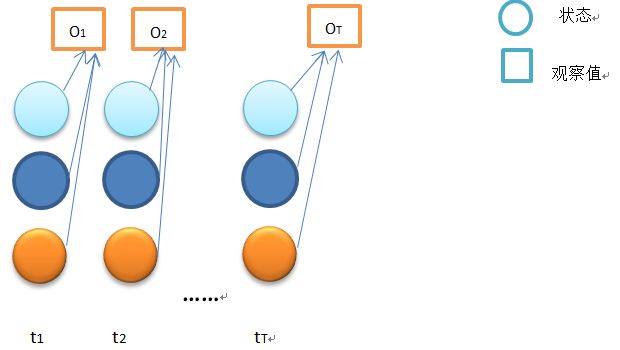
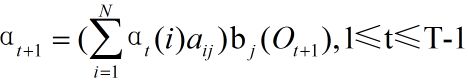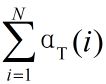      隐马模型的评估问题即，在已知一个观察序列O=O₁O₂...O_T，和模型μ=（A,B,π}的条件下，观察序列O的概率，即P(O|μ}

                  

      如果穷尽所有的状态组合，即S₁S₁...S₁, S₁S₁...S₂, S₁S₁...S₃, ..., S₃S₃...S₃。这样的话t₁时刻有N个状态，t₂时刻有N个状态...t_T时刻有N个状态，这样的话一共有N*N*...*N= N^T种组合，时间复杂度为O(N^T),计算时，就会出现“指数爆炸”，当T很大时，简直无法计算这个值。为解决这一问题，Baum提出了前向算法。

      归纳过程

      首先引入前向变量α_t(i):在时间t时刻，HMM输出序列为O₁O₂...O_T,在第t时刻位于状态s_i的概率。

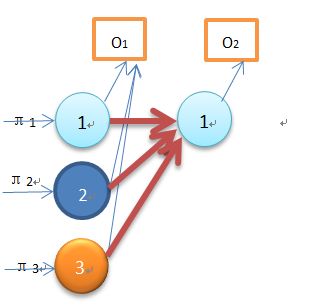
      当T=1时，输出序列为O₁,此时计算概率为P(O₁|μ）：假设有三个状态（如下图）1、2、3，输出序列为O₁，有三种可能一是状态1发出，二是从状态2发出，三是从状态3发出。另外从状态1发出观察值O₁得概率为b₁(O₁),从状态2发出观察值O₁得概率为b₂(O₁),从状态3发出观察值O₁得概率为b₃(O₁)。因此可以算出

     P(O₁|μ）= π₁*b₁(O₁)+π₂*b₂(O₁) +  π₃*b₃(O₁)= α₁(1) + α₁(2) + α₁(3)

                                    

      当T=2时，输出序列为O₁O₂,此时计算概率为P(O₁O₂|μ）：假设有三个状态（如下图）1、2、3，输出序列为O₁，有三种可能一是状态1发出，二是从状态2发出，三是从状态3发出。另外从状态1发出观察值O₂得概率为b₁(O₂),从状态2发出观察值O₂得概率为b₂(O₂),从状态3发出观察值O₂得概率为b₃(O₂)。

      要是从状态1发出观察值O₂，可能从第一时刻的1、2或3状态装换过来，要是从状态1转换过来，概率为α₁(1)*a₁₁*b₁(O₂),要是从状态2转换过来，概率为α₁(2)*a₂₁*b₁(O₂),要是从状态3转换过来，概率为α₁(3)*a₃₁*b₁(O₂),因此

     P(O₁O_2,q₂₌s₁|μ）= α₁(1)*a₁₁*b₁(O₂)  + α₁(2)*a₂₁*b₁(O₂) + α₁(3)*a₃₁*b₁(O₂)=α₂(1)

                                    

      同理：P(O₁O_2,q₂₌s₁|μ）= α₁(1)*a₁₂*b₂(O₂)  + α₁(2)*a₂₂*b₂(O₂) + α₁(3)*a₃₂*b₂(O₂)=α₂(2)

               P(O₁O_2,q₂₌s₁|μ）= α₁(1)*a₁₃*b₁(O₂)  + α₁(2)*a₂₃*b₃(O₂) + α₁(3)*a₃₃*b₃(O₂)=α₂(3)

     所以：P(O₁O₂|μ）=P(O₁O_2,q₂₌s₁|μ）+ P(O₁O_2,q₂₌s₁|μ）+ P(O₁O_2,q₂₌s₁|μ）

                             =α₂(1) + α₂(2) + α₂(3)

      以此类推。。。

      前向算法

       step1 初始化：α₁(i) = π_i*b_i(O₁), 1≤i≤N

       step2 归纳计算:

                          

       step3 终结：

                      P(O|μ）=

      时间复杂度

      计算某时刻的某个状态的前向变量需要看前一时刻的N个状态，此时时间复杂度为O(N),每个时刻有N个状态，此时时间复杂度为N*O(N)=O(N²),又有T个时刻，所以时间复杂度为T*O(N²)=O(N²T)。

      程序例证

      

        前向算法计算P(O|M)：

        step1：α₁(1) =π₁*b₁(red)=0.2*0.5=0.1          α₁(2)=π₂*b₂(red)==0.4*0.4= 0.16          α₁(3)=π₃*b₃(red)==0.4*0.7=0.21

        step2：α₂(1)=α₁(1)*a₁₁*b₁(white) + α₁(2)*a₂₁*b₁(white) + α₁(3)*a₃₁*b₁(white)

                     ...

        step3:P(O|M) = α₃(1)+α₃(2)+α₃(3)

        程序代码

#include 
#include 
#include <string.h>

int main()
{
        float a[3][3] = {{0.5,0.2,0.3},{0.3,0.5,0.2},{0.2,0.3,0.5}};
        float b[3][2] = {{0.5,0.5},{0.4,0.6},{0.7,0.3}};
        float alpha[4][3];
        int i,j,k, count = 1;
        //output list
        int list[4] = {0,1,0,1};
        //step1:Initialization
        alpha[0][0] = 0.2 * 0.5;
        alpha[0][1] = 0.4 * 0.4;
        alpha[0][2] = 0.4 * 0.7;
        //step2:iteration
        for (i=1; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                alpha[i][j] = 0;
                for(k=0; k<=2; k++)
                {
                   alpha[i][j] += alpha[i-1][k] * a[k][j] * b[j][list[count]];
                }
            }
            count += 1;
        }
       for (i=0; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("a[%d][%d]=%f\n",i+1,j+1,alpha[i][j]);
            }
        }
       //step3:end
       printf("Forward:%f\n", alpha[3][0]+alpha[3][1]+alpha[3][2]);
       return 0;
}

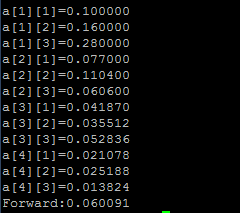
     运行结果