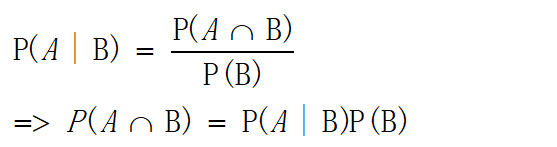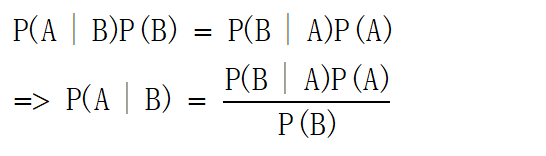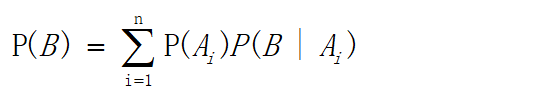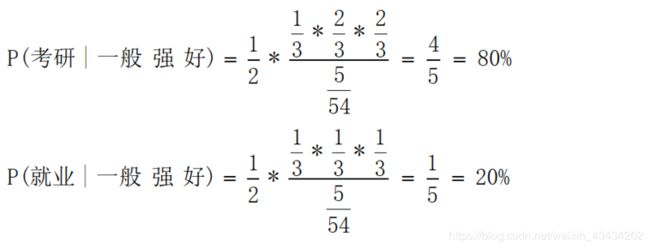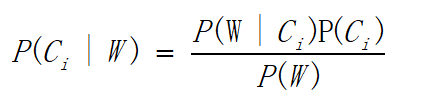一、算法概述
贝叶斯算法是基于统计学的一种概率分类方法,而朴素贝叶斯是其中最简单的一种;朴素贝叶斯属于监督学习的算法之一,一般用来解决分类问题,我们之所以称之为"朴素",是因为整个形势化过程只做最原始、最简单的假设,即假设数据集所有的样本之间都是独立存在,互不影响的。
用一个条件概率公式更好的理解这个假设条件,假设一个样本中有(a1、a2、a3、... an)共n个样本,若有P(a1,a2,a3,...,an) = P(a1) P(a2) P(a3)...P(an),则称该数据集中各个样本之间独立存在。
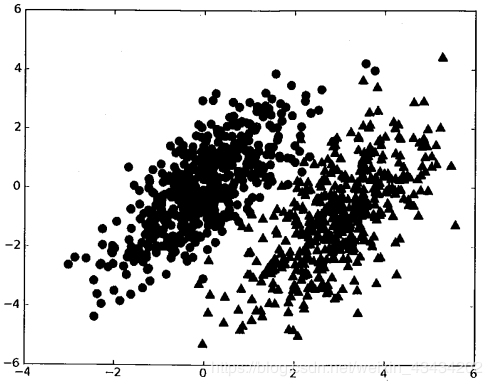
假设我们有一个数据集,共有两个特征,分别为三角形和圆形,如下图所示:
若用P1(x,y)表示数据点(x,y)属于圆形的概率,用P2(x,y)表示数据点(x,y)属于三角形的概率,那么对于一个新数据点(x,y),可以用以下规则判断其类别:
- 若P1(x,y)>P2(x,y),那么该点类别为1
- 若P1(x,y)
总得来说,未知属性的类别趋向概率高的。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
二、条件概率公式
条件概率公式是概率论中十分基础的一个公式,即在事件B发生的情况下,事件A也发生的概率,如下文氏图:
通过这幅文氏图,在在事件B发生的情况下,事件A也发生的概率如下
同理可得
最后推得条件概率的计算公式如下
这个公式被称为贝叶斯准则,它告诉我们如何交换条件概率中的条件和结果,例如已知P(B | A),如何计算P(A | B)。
这里有几个概念需要了解:
- P(A)称为"先验概率",即在事件B发生之间对事件A发生概率的判断。
- P(A | B)称为"后验概率",即在事件B发生之后对事件A发生概率的再次判断。
- P(B | A)/P(B)称为"可能性函数",这是一个调整因子,可以帮助预估概率更加接近真实概率。
所以条件概率也可以理解成:
后验概率 = 先验概率 * 调整因子
其中"调整因子"的值对条件概率的影响如下:
- 当"调整因子"小于1时,"先验概率"被减弱,事件A的发生的概率变小
- 当"调整因子"等于1时,"先验概率"不变,对事件A的发生概率无影响
- 当"调整因子"大于1时,"先验概率"被增强,事件A的发生的概率变大
三、条件概率实例
再有一年半,偶也要面临考研or就业的抉择,向周围同学询问了他们的选择,得到这么一份小数据集,偶也总结了一下自身条件,学习成绩一般、自学能力不错、家里的经济条件也允许,那我是选择考研还是就业呢?
| 成绩 | 自学能力 | 家庭条件 | 选择 |
|---|---|---|---|
| 学霸 | 强 | 好 | 考研 |
| 一般 | 强 | 差 | 考研 |
| 学渣 | 弱 | 好 | 考研 |
| 学霸 | 强 | 差 | 就业 |
| 一般 | 弱 | 好 | 就业 |
| 学渣 | 弱 | 差 | 就业 |
对于这个例子,按照贝叶斯公式进行求解,可以转化成P(考研 | 一般 强 好)和P(就业 | 一般 强 好)两类,因为贝叶斯的思想就是根据最高概率判断类别。
"先验概率"P(考研)很容易计算,但是"可能性函数"中的分母P(一般 强 好)却不知如何计算,这里需要引入一个新的公式——全概率公式。
所以依据全概率公式P(一般 强 好)求值公式如下:
最后依据贝叶斯准则可计算二者的概率:
其中考研的概率为80%,就业的概率为20%,所以就我自己的条件而言,该算法将我分配至考研党中。我们从小学就学过一个道理,分母相同的两个分数,分子大的分数大,因为朴素贝叶斯的思想是要依据概率判断类别,所以就可以省去计算全概率这一步,在编写程序的时候可以提高效率。
四、文本分类
从文本中获取特征,需先将文本拆分。这里的特征是来自文本的词条,一个词条是字符的任意组合。对于文本而言,可以将词条想象成单词;对于IP地址而言,又可以将词条想象成两个点间的数字组合,不同类型的文本,词条的类型可以不同。然后将每一个文本片段表示为一个词条向量,其中值为1表示词条出现在文档中,0则表示词条未出现。
平时在刷微博的时候,不管事情好与坏,评论总是有好有坏,因为避免不了总有杠精的存在。构建一个快速过滤器,这个过滤器的功能就是分类好坏评论,如果某条评论使用了负面或者侮辱性的语言,则将该评论判定为侮辱类评论,反之则将其归为非侮辱类评论,其中侮辱类用1表示,非侮辱类用0表示。
4.1构建词向量
假设我们已经获取到文本数据,先考虑出现在文本中的所有单词,决定将哪些词纳入词汇表或者说所要的词汇集合,然后将文本中的句子转化为向量,以方便对文本中每句话的类别进行判断。
#设置文本数据集
def loadDataSet():
#文本语句切分
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
#类别标签的向量
classVec = [0,1,0,1,0,1]
return postingList,classVec loadDataSet函数创建了实验文本,主要的操作是将每一句话切分成若干个单词,并且创建了一个类别标签列表,其中1代表侮辱类,0代表非侮辱类,是通过人的判断后进行标注。
#创建词汇表
def createVocabList(dataSet):
#创建一个空的不重复列表
vocabSet = set([])
for document in dataSet:
#取两者并集
vocabSet = vocabSet | set(document)
return list(vocabSet)
#判断
def setOfWords2Vec(vocabList, inputSet):
#创建一个元素都为0的向量
returnVec = [0] * len(vocabList)
for word in inputSet:
if word in vocabList:
#若词汇表包含该词汇,则将该位置的0变为1
returnVec[vocabList.index(word)] = 1
return returnVec
#将所有词条向量汇总
def get_Mat(inputSet):
trainMat = [] #创建空列表
vocabList = createVocabList(inputSet)
#遍历输入文本,将每个词条向量加入列表中
for Set in inputSet:
returnVec = setOfWords2Vec(vocabList,Set)
trainMat.append(returnVec)
return trainMatcreateVocabList函数的作用是通过set方法已经取并集的方式返回一个包含文本中所有出现的不重复词的集合;setOfWords2Vec函数的输入参数为词汇表和某个文本,输出的是文本向量,向量的元素包括1或0,分别表示词汇表中的单词是否出现在输入的文本中,思路是首先创建一个同词汇表等长的向量,并将其元素都设置为0,然后遍历输入文本的单词,若词汇表中出现了本文的单词,则将其对应位置上的0置换为1。
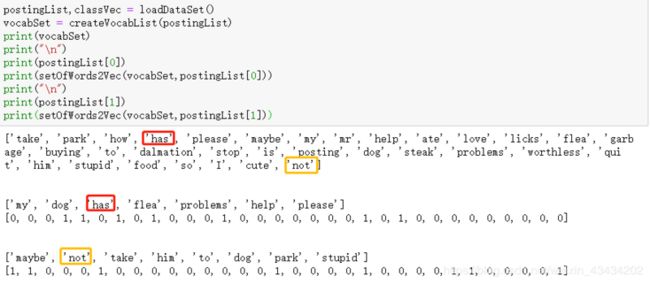
代码运行截图如下
例如词汇表中第四个单词has在第一个输入文本中出现,则向量中的第4个元素置为1;同理词汇表中最后一个单词not在第二个输入文本中出现,则向量中最后一个元素置为1。
4.2训练算法
这里如果重写上文提过的贝叶斯准则,W为一个向量,它由多个数值组成,Ci代表类别,即侮辱类or非侮辱类,公式如下:
若使用上述公式对一个未知类进行判断,我们只需比较两个两个概率值的大小即可,首先通过类别i的文本数除以总文本数可以计算出P(Ci)的数值;然后计算P(W | Ci),因为W可以展开为一个个独立特征,那么P(W0,W1,W2...Wn | Ci) = P(W0 | Ci)P(W1 | Ci)P(W2 | Ci)...P(Wn | Ci),简化了计算的过程。
代码如下:
def trainNB(trainMatrix,trainCategory):
#训练文本数量
numTrainDocs = len(trainMatrix)
#每篇文本的词条数
numWords = len(trainMatrix[0])
#文档属于侮辱类(1)的概率
pAbusive = sum(trainCategory)/float(numTrainDocs)
#创建两个长度为numWords的零数组
p0Num = np.zeros(numWords)
p1Num = np.zeros(numWords)
#分母初始化
p0Denom = 0.0
p1Denom = 0.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
#统计侮辱类的条件概率所需的数据,即P(w0|1),P(w1|1),P(w2|1)···
p1Num += trainMatrix[i]
#print(p1Num)
p1Denom += sum(trainMatrix[i])
#print(p1Num)
else:
#统计非侮辱类的条件概率所需的数据,即P(w0|0),P(w1|0),P(w2|0)···
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
#计算词条出现的概率
p1Vect = p1Num/p1Denom
p0Vect = p0Num/p0Denom
return p0Vect,p1Vect,pAbusivetrainNB函数的输入参数包括文本矩阵trainMatrix和每个词条的类别标签所构成的向量trainCategory。首先文本属于侮辱类的概率只需要将侮辱性词条的个除以总词条个数即可;计算P(W | C1)和P(W | C0)时,需要将其分子和分母初始化,遍历输入文本时,一旦某个词语(侮辱性or非侮辱性)在某一文档中出现,则该词对应的个数(p1Num或p0Num)就加1,并且在总文本中,该词条的总次数也相应加1。
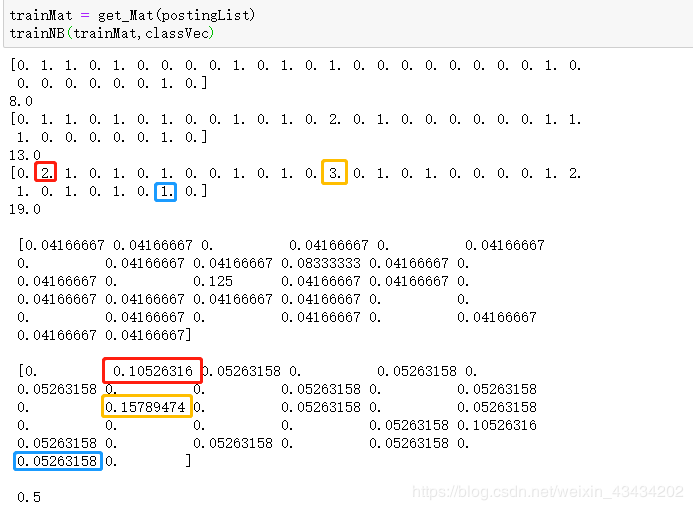
代码运行截图如下
这里打印出属于侮辱性的词条,当不同词条出现同一词语时,会在词条向量的同一位置上累加,最后每一个词语出现的次数除以总数就得到了相应的概率,例如出现两次—>0.105、出现三次—>0.157、出现一次—>0.052。
4.3测试算法
def classifyNB(vec2Classify, p0V,P1V,PAb):
#将对应元素相乘
p1 = reduce(lambda x,y:x*y, vec2Classify * p1V) * pAb
p0 = reduce(lambda x,y:x*y, vec2Classify * p0V) * (1.0 - PAb)
print('p0:',p0)
print('p1:',p1)
if p1 > p0:
return 1
else:
return 0classifyNB函数传入的4个参数分别为测试文本的向量以及训练函数trainNB返回的三个参数,其作用是将文本的向量与p1V和p2V分别对应相乘,并乘以pAb和其二分类对应概率(1.0-pAb),然后比较p1与p2的大小判别出测试文本属于属于哪一类,这里举一个reduce方法的小例子,方便理解。
reduce(lambda x,y:x+y,[1,2,3,4])
'''
10
'''reduce方法是将两个元素以某种操作运算符为条件归并成一个结果,并且它是一个迭代的过程,每次调用该方法直至得到最后一个结果,例如上面数组[1,2,3,4]以加法为操作运算实现1+2;3+3;6+4 = 10的操作过程。
下面通过调用前文的函数,对测试数据进行分类操作,代码如下:
def testingNB(testVec):
#创建实验样本
postingList,classVec = loadDataSet()
#创建词汇表
vocabSet = createVocabList(postingList)
#将实验样本向量汇总
trainMat = get_Mat(postingList)
#训练算法
p0V,P1V,PAb = trainNB(trainMat,classVec)
#将测试文本向量化
The_test = setOfWords2Vec(vocabSet,testVec)
#判断类别
if classifyNB(The_test,p0V,P1V,PAb):
print(testVec,"侮辱类")
else:
print(testVec,"非侮辱类")传入测试数据testVec,并返回分类结果如下图:
哎呀,这stupid怎么还能被判断成非侮辱类了呢?会不会是程序变蠢了?程序是正常的,但是需要对程序做一点改进,我们都知道0是一个特别牛皮的数,因为不论什么数字乘以0结果都得0,所以只要p1V向量和测试向量有一个对应位置上同时都为0,那么最终结果一定为0。为了降低上述影响,可以将所有词的出现数初始化为1,并将分母初始化为2,这种方法被称为拉普拉斯平滑。
这部分对trainNB函数做以下更改:
p0Num = np.ones(numWords)
p1Num = np.ones(numWords)
p0Denom = 2.0
p1Denom = 2.0除此之外,还有一个问题是下溢出,什么是下溢出呢?在许多很小的数相乘时,当计算乘积 P(W0 | Ci)P(W1 | Ci)P(W2 | Ci)...P(Wn | Ci)时,由于大部分因子都非常小,所以程序会下溢出或者得不到正确答案,比如程序会将乘积非常小的结果四舍五入后得到0,一种经典的解决办法是取乘积的自然对数。
在代数中有ln(a*b) = ln(a)+ln(b),由乘法转为加法后,就可以避免下溢出或者浮点数舍入导致的错误,有人可能会担心,二者计算出的结果是有差异的,这是事实,但是对于我们所需要的分类结果是无影响的。
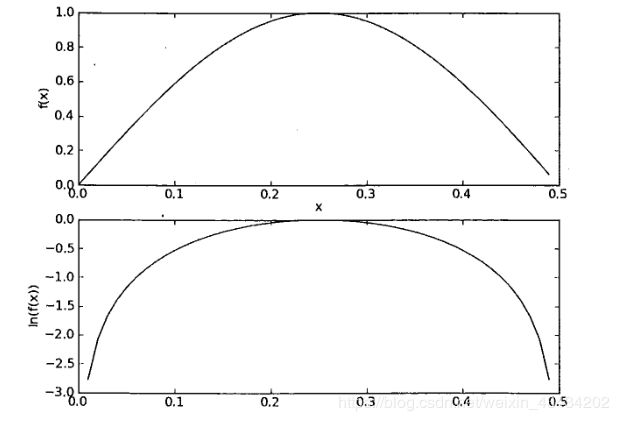
f(x)与ln(x)的曲线如下图:
通过观察这两条曲线会发现它们在相同的区域同时增加或同时减少,并且在相同点取到极值,虽然二者的极值不同,但不影响最终结果,因为我们只需通过比较二者值的大小来判断测试数据的类别。
这部分对trainNB函数做以下更改:
p1Vect = np.log(p1Num/p1Denom)
p0Vect = np.log(p0Num/p0Denom)前面计算概率时做了取对数操作,由于log(a*b) = log(a)+log(b),所以可以对classifyNB函数进行改进,用sum方法代替reduce方法即可。
具体代码如下:
def classifyNB(ClassifyVec, p0V,p1V,pAb):
#p1 = reduce(lambda x,y:x*y, ClassifyVec * p1V) * pAb
#p0 = reduce(lambda x,y:x*y, ClassifyVec * p0V) * (1.0 - PAb)
#将对应元素相乘
p1 = sum(ClassifyVec * p1V) + np.log(pAb)
p0 = sum(ClassifyVec * p0V) + np.log(1.0 - pAb)
print('p0:',p0)
print('p1:',p1)
if p1 > p0:
return 1
else:
return 0最后测试整体代码运行截图如下:
通过p0与p1的比较,可以正确的将测试文本进行分类,stupid最后被判定为侮辱类,看来程序是不会变蠢的,会变蠢的是我。
4.4词袋模型拓展
前面程序中,我们将每个次的出现与否作为一个特征,这可以被描述为词集模型。如果一个词在文本中出现不止一次,不能将其单纯的作为特征同等看待,因为其中涉及到了权重不同,这种方法被称为词袋模型。在词袋中,每个单词可以出现若干次,而在词集中,每个词只能出现一次。可以在词集模型的基础上加以修改,将其转换成词袋模型。
代码如下:
def setOfWords2Vec(vocabList, inputSet):
#创建一个元素都为0的向量
returnVec = [0] * len(vocabList)
for word in inputSet:
if word in vocabList:
#若每当文本中出现词汇表中的单词一次,就将该位置的数字加1
returnVec[vocabList.index(word)] += 1
return returnVec五、文末总结
朴素贝叶斯对应优点如下:
- 可以处理样本较少的数据集
- 可以处理多类别问题
- 对缺失数据不太敏感
- 适合进行文本分类
朴素贝叶斯对应缺点如下:
- 对于输入数据的表达方式敏感
- 需要假设数据中每个特征之间需要独立
- 先验模型建立不当可能导致预测结果不佳
本文就朴素贝叶斯该算法的原理进行简单介绍,下篇文章会介绍朴素贝叶斯的应用实例。
关注公众号【奶糖猫】后台回复“Bayes”可获取源码供参考,感谢阅读。