TensorFlow 2.0深度学习算法实战---第13章 生成对抗网络

我不能创造的事物，我就还没有完全理解它。−理查德·費曼

在生成对抗网络(Generative Adversarial Network，简称 GAN)发明之前，变分自编码器被认为是理论完备，实现简单，使用神经网络训练起来很稳定，生成的图片逼近度也较高，但是人眼还是可以很轻易地分辨出真实图片与机器生成的图片。

2014 年，Université de Montréal 大学 Yoshua Bengio(2019 年图灵奖获得者)的学生 Ian Goodfellow 提出了生成对抗网络 GAN，从而开辟了深度学习最炙手可热的研究方向之一。从 2014 年到 2019 年，GAN 的研究稳步推进，研究捷报频传，最新的 GAN 算法在图片生成上的效果甚至达到了肉眼难辨的程度，着实令人振奋。由于 GAN 的发明，IanGoodfellow 荣获 GAN 之父称号，并获得 2017 年麻省理工科技评论颁发的 35 Innovators Under 35 奖项。图 13.1 展示了从 2014 年到 2018 年，GAN 模型取得了图书生成的效果，可以看到不管是图片大小，还是图片逼真度，都有了巨大的提升。

接下来，我们将从生活中博弈学习的实例出发，一步步引出 GAN 算法的设计思想和模型结构。

13.1 博弈学习实例

我们用一个漫画家的成长轨迹来形象介绍生成对抗网络的思想。考虑一对双胞胎兄弟，分别称为老二 G 和老大 D，G 学习如何绘制漫画，D 学习如何鉴赏画作。还在娃娃时代的两兄弟，尚且只学会了如何使用画笔和纸张，G 绘制了一张不明所以的画作，如图13.2(a)所示，由于此时 D 鉴别能力不高，觉得 G 的作品还行，但是人物主体不够鲜明。在D 的指引和鼓励下，G 开始尝试学习如何绘制主体轮廓和使用简单的色彩搭配。

一年后，G 提升了绘画的基本功，D 也通过分析名作和初学者 G 的作品，初步掌握了鉴别作品的能力。此时 D 觉得 G 的作品人物主体有了，如图 13.2(b)，但是色彩的运用还不够成熟。数年后，G 的绘画基本功已经很扎实了，可以轻松绘制出主体鲜明、颜色搭配合适和逼真度较高的画作，如图13.2©，但是 D 同样通过观察 G 和其它名作的差别，提升了画作鉴别能力，觉得 G 的画作技艺已经趋于成熟，但是对生活的观察尚且不够，作品没有传达神情且部分细节不够完美。又过了数年，G 的绘画功力达到了炉火纯青的地步，绘制的作品细节完美、风格迥异、惟妙惟肖，宛如大师级水准，如图 13.2(d)，即便此时的D 鉴别功力也相当出色，亦很难将 G 和其他大师级的作品区分开来。

上述画家的成长历程其实是一个生活中普遍存在的学习过程，通过双方的博弈学习，相互提高，最终达到一个平衡点。GAN 网络借鉴了博弈学习的思想，分别设立了两个子网络：负责生成样本的生成器 G 和负责鉴别真伪的鉴别器 D。类比到画家的例子，生成器 G就是老二，鉴别器 D 就是老大。鉴别器 D 通过观察真实的样本和生成器 G 产生的样本之间的区别，学会如何鉴别真假，其中真实的样本为真，生成器 G 产生的样本为假。而生成器 G 同样也在学习，它希望产生的样本能够获得鉴别器 D 的认可，即在鉴别器 D 中鉴别为真，因此生成器 G 通过优化自身的参数，尝试使得自己产生的样本在鉴别器 D 中判别为真。生成器 G 和鉴别器 D 相互博弈，共同提升，直至达到平衡点。此时生成器 G 生成的样本非常逼真，使得鉴别器 D 真假难分。

在原始的 GAN 论文中，Ian Goodfellow 使用了另一个形象的比喻来介绍 GAN 模型：生成器网络 G 的功能就是产生一系列非常逼真的假钞试图欺骗鉴别器 D，而鉴别器 D 通过学习真钞和生成器 G 生成的假钞来掌握钞票的鉴别方法。这两个网络在相互博弈的过程中间同步提升，直到生成器 G 产生的假钞非常的逼真，连鉴别器 D 都真假难辨。

这种博弈学习的思想使得 GAN 的网络结构和训练过程与之前的网络模型略有不同，下面我们来详细介绍 GAN 的网络结构和算法原理。

13.2 GAN 原理

现在我们来正式介绍生成对抗网络的网络结构和训练方法。

13.2.1 网络结构

生成对抗网络包含了两个子网络：生成网络(Generator，简称 G)和判别网络(Discriminator，简称 D)，其中生成网络 G 负责学习样本的真实分布，判别网络 D 负责将生成网络采样的样本与真实样本区分开来。

生成网络G() 生成网络 G 和自编码器的 Decoder 功能类似，从先验分布(∙)中采样隐藏变量~(∙)，通过生成网络 G 参数化的$p_g(x|z)$分布，获得生成样本$\mathbf{x}\sim p_g(\mathbf{x}|\mathbf{z})$如图13.3 所示。其中隐藏变量的先验分布(∙)可以假设为某中已知的分布，比如多元均匀分布$z\sim$ Uniform (-1,1)。

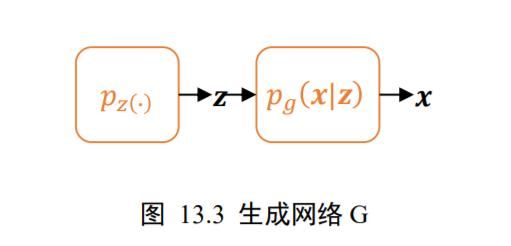
$p_g(x|z)$可以用深度神经网络来参数化，如下图 13.4 所示，从均匀分布(∙)中采样出隐藏变量，经过多层转置卷积层网络参数化的$p_g(x|z)$分布中采样出样本$x_f$。从输入输出层面来看，生成器 G 的功能是将隐向量通过神经网络转换为样本向量$x_f$，下标代表假样本(Fake samples)。

判别网络D() 判别网络和普通的二分类网络功能类似，它接受输入样本的数据集，包含了采样自真实数据分布$p_r(\cdot )$的样本$x_r\sim p_r(\cdot )$，也包含了采样自生成网络的假样本${\mathbf{x}}_f\sim p_g(\mathbf{x}|\mathbf{z})$，$x_r$和$x_f$共同组成了判别网络的训练数据集。判别网络输出为属于真实样本的概率(为真|)，我们把所有真实样本$x_r$的标签标注为真(1)，所有生成网络产生的样本$x_f$标注为假(0)，通过最小化判别网络 D 的预测值与标签之间的误差来优化判别网络参数，如图 13.5 所示。

13.2.2 网络训练

GAN 博弈学习的思想体现在在它的训练方式上，由于生成器 G 和判别器 D 的优化目标不一样，不能和之前的网络模型的训练一样，只采用一个损失函数。下面我们来分别介绍如何训练生成器 G 和判别器 D。

对于判别网络 D，它的目标是能够很好地分辨出真样本$x_r$与假样本$x_f$。以图片生成为例，它的目标是最小化图片的预测值和真实值之间的交叉熵损失函数：
$$\underset{\theta }{\min }\mathcal{L}=\mathrm{CE}\left(D_{\theta }\left({\mathbf{x}}_r\right),y_r,D_{\theta }\left({\mathbf{x}}_f\right),y_f\right)$$
其中$D_{\theta }\left({\mathbf{x}}_r\right)$代表真实样本$x_r$在判别网络$D_{\theta }$的输出，为判别网络的参数集，$D_{\theta }\left({\mathbf{x}}_f\right)$为生成样本$x_f$在判别网络的输出，$y_r$为$x_r$的标签，由于真实样本标注为真，故$y_r$ = 1，$y_f$为生成样本的$x_f$的标签，由于生成样本标注为假，故$y_f$ = 0。CE函数代表交叉熵损失函数CrossEntropy。二分类问题的交叉熵损失函数定义为：
$$\mathcal{L}=-\sum _{x_r\sim p_r()}\log D_{\theta }\left(x_r\right)-\sum _{x_f\sim p_g(\cdot )}\log \left(1-D_{\theta }\left(x_f\right)\right)$$
因此判别网络 D 的优化目标是：
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmin}}-\sum _{x_r\sim p_r(\cdot )}\log D_{\theta }\left(x_r\right)-\sum _{x_f\sim p_g(\cdot )}\log \left(1-D_{\theta }\left(x_f\right)\right)$$
把${\min }_{\theta }\mathcal{L}$问题转换为${\max }_{\theta }-\mathcal{L}$，并写成期望形式：
$${\theta }^{\ast }=\underset{\theta }{\mathrm{argmax}}{\mathbb{E}}_{x_r\sim p_r(\cdot )}\log D_{\theta }\left(x_r\right)+{\mathbb{E}}_{x_f\sim p_g(\cdot )}\log \left(1-D_{\theta }\left(x_f\right)\right)$$
对于生成网络G()，我们希望$x_f=G(z)$能够很好地骗过判别网络 D，假样本$x_f$在判别网络的输出越接近真实的标签越好。也就是说，在训练生成网络时，希望判别网络的输出(())越逼近 1 越好，最小化(())与 1 之间的交叉熵损失函数：
$$\underset{\varphi }{\min }\mathcal{L}=CE\left(D\left(G_{\varphi }(\mathbf{z})\right),1\right)=-\log D\left(G_{\varphi }(\mathbf{z})\right)$$
把${\min }_{\varphi }\mathcal{L}$问题转换成${\max }_{\varphi }-\mathcal{L}$，并写成期望形式：
$${\varphi }^{\ast }=\underset{\varphi }{\mathrm{argmax}}{\mathbb{E}}_{\mathbf{z}\sim p_z(\cdot )}\log D\left(G_{\varphi }(\mathbf{z})\right)$$
再次等价转化为：
$${\varphi }^{\ast }=\underset{\varphi }{\mathrm{argmin}}\mathcal{L}={\mathbb{E}}_{\mathbf{z}\sim p_z(\cdot )}\log \left[1-D\left(G_{\varphi }(\mathbf{z})\right)\right]$$
其中为生成网络 G 的参数集，可以利用梯度下降算法来优化参数。

13.2.3 统一目标函数

我们把判别网络的目标和生成网络的目标合并，写成min − max博弈形式：
$$\underset{\varphi }{\min }\underset{\theta }{\max }\mathcal{L}(D,G)={\mathbb{E}}_{x_r\sim p_r(\cdot )}\log D_{\theta }\left({\mathbf{x}}_r\right)+{\mathbb{E}}_{{\mathbf{x}}_f\sim p_g(\cdot )}\log \left(1-D_{\theta }\left({\mathbf{x}}_f\right)\right)$$
$$={\mathbb{E}}_{\mathbf{x}\sim p_{\mathbf{r}}(\mathbf{c})}\log D_{\mathbf{\theta }}(\mathbf{x})+{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\cdot )}\log \left(1-D_{\mathbf{\theta }}\left(G_{\mathbf{\varphi }}(\mathbf{z})\right)\right)$$

算法流程如下：

13.3 DCGAN 实战

本节我们来完成一个二次元动漫头像图片生成实战，参考 DCGAN 的网络结构，其中判别器 D 利用普通卷积层实现，生成器 G 利用转置卷积层实现，如图 13.6 所示。

13.3.1 动漫图片数据集

这里使用的是一组二次元动漫头像的数据集，共 51223 张图片，无标注信息，图片主体已裁剪、对齐并统一缩放到96 × 96大小，部分样片如图 13.7 所示。

数据集下载地址：https://github.com/chenyuntc/pytorch-book/tree/master/chapter07-AnimeGAN

对于自定义的数据集，需要自行完成数据的加载和预处理工作，我们这里聚焦在 GAN算法本身，后续自定义数据集一章会详细介绍如何加载自己的数据集，这里直接通过预编写好的make_anime_dataset函数返回已经处理好的数据集对象。代码如下：

img_path = glob.glob(r'C:\Users\z390\Downloads\faces\*.jpg')
# 构建数据集对象，返回数据集 Dataset 类和图片大小
dataset, img_shape, _ = make_anime_dataset(img_path, batch_size,resize=64)

其中 dataset 对象就是 tf.data.Dataset 类实例，已经完成了随机打散、预处理和批量化等操作，可以直接迭代获得样本批，img_shape 是预处理后的图片大小。

13.3.2 生成器

生成网络 G 由 5 个转置卷积层单元堆叠而成，实现特征图高宽的层层放大，特征图通道数的层层减少。首先将长度为 100 的隐藏向量通过 Reshape 操作调整为[, 1,1,100]的 4维张量，并依序通过转置卷积层，放大高宽维度，减少通道数维度，最后得到高宽为 64，通道数为 3 的彩色图片。每个卷积层中间插入 BN 层来提高训练稳定性，卷积层选择不使用偏置向量。生成器的类代码实现如下：

class Genetator(keras.Model):
    #生成器网络类
    def __init__(self):
        super(Genetator,self).__init__()
        filter=64
        #转置卷积层1，输出channel为filter*8,核大小4，步长1，不使用padding，不使用偏置
        self.conv1=layers.Conv2DTranspose(filter*8,4,1,'valid',use_bias=False)
        self.bn1=layers.BatchNormalization()
        #转置卷积层2
        self.conv2=layers.Conv2DTranspose(filter*4,4,2,'same',use_bias=False)
        self.bn2=layers.BatchNormalization()
        #转置卷积层3
        self.conv3=layers.Conv2DTranspose(filter*2,4,2,'same',use_bias=False)
        self.bn3=layers.BatchNormalization()
        #转置卷积层4
        self.conv4=layers.Conv2DTranspose(filter*1,4,2,'same',use_bias=False)
        self.bn4=layers.BatchNormalization()
        #转置卷积层5
        self.conv5=layers.Conv2DTranspose(3,4,2,'same',use_bias=False)

生成网络 G 的前向传播过程实现如下：

    def call(self,inputs,training=None):
        x=inputs#[z,100]
        # reshape成4D张量，方便后续转换卷积运算：(b,1,1,100)
        x=tf.reshape(x,(x.shape[0],1,1,x.shape[1]))
        x=tf.nn.relu(x)#激活函数
        #转置卷积-BN-激活函数：(b,4,4,512)
        x=tf.nn.relu(self.bn1(self.conv1(x),training=training))
        # 转置卷积-BN-激活函数：(b,8,8,256)
        x=tf.nn.relu(self.bn2(self.conv2(x),training=training))
        # 转置卷积-BN-激活函数：(b,16,16,128)
        x=tf.nn.relu(self.bn3(self.conv3(x), training=training))
        # 转置卷积-BN-激活函数：(b,32,32,64)
        x=tf.nn.relu(self.bn4(self.conv4(x), training=training))
        # 转置卷积-BN-激活函数：(b,64,64,3)
        x = self.conv5(x)
        x=tf.tanh(x)#输出x范围[-1~1],与预处理一致

        return x

生成网络的输出大小为[, 64,64,3]的图片张量，数值范围为[−1~1]。

13.3.3 判别器

判别网络 D 与普通的分类网络相同，接受大小为[, 64,64,3]的图片张量，连续通过 5个卷积层实现特征的层层提取，卷积层最终输出大小为[, 2,2,1024]，再通过池化层GlobalAveragePooling2D将特征大小转换为[, 1024]，最后通过一个全连接层获得二分类任务的概率。判别网络 D 类的代码实现如下：

class Discriminator(keras.Model):
    #判别器类
    def __init__(self):
        super(Discriminator,self).__init__()
        filter=64
        #卷积层1
        self.conv1=layers.Conv2D(filter,4,2,'valid',use_bias=False)
        self.bn1=layers.BatchNormalization()
        # 卷积层2
        self.conv2=layers.Conv2D(filter*2, 4, 2, 'valid', use_bias=False)
        self.bn2 = layers.BatchNormalization()
        # 卷积层3
        self.conv3 = layers.Conv2D(filter*4, 4, 2, 'valid', use_bias=False)
        self.bn3 = layers.BatchNormalization()
        # 卷积层4
        self.conv4 = layers.Conv2D(filter*8, 3, 1, 'valid', use_bias=False)
        self.bn4 = layers.BatchNormalization()
        # 卷积层5
        self.conv5= layers.Conv2D(filter*16, 3, 1, 'valid', use_bias=False)
        self.bn5 = layers.BatchNormalization()
        #全局池化层
        self.pool=layers.GlobalAveragePooling2D()
        #特征打平层
        self.flatten=layers.Flatten()
        #2分类全连接层
        self.fc=layers.Dense(1)

判别器 D 的前向计算过程实现如下：

    def call(self,inputs,training=None):
        #卷积-BN-激活函数：(b,31,31,64)
        x=tf.nn.leaky_relu(self.bn1(self.conv1(inputs),training=training))
        # 卷积-BN-激活函数：(b,14,14,128)
        x = tf.nn.leaky_relu(self.bn2(self.conv2(inputs), training=training))
        # 卷积-BN-激活函数：(b,6,6,256)
        x = tf.nn.leaky_relu(self.bn3(self.conv3(inputs), training=training))
        # 卷积-BN-激活函数：(b,4,4,512)
        x = tf.nn.leaky_relu(self.bn4(self.conv4(inputs), training=training))
        # 卷积-BN-激活函数：(b,2,2,1024)
        x = tf.nn.leaky_relu(self.bn5(self.conv5(inputs), training=training))
        # 卷积-BN-激活函数：(b,1024)
        x = self.pool(x)
        #打平
        x=self.flatten(x)
        #输出，[b,1024]=>[b,1]
        logits=self.fc(x)
        return logits

判别器的输出大小为[, 1]，类内部没有使用 Sigmoid 激活函数，通过 Sigmoid 激活函数后可获得个样本属于真实样本的概率。

13.3.4 训练与可视化

判别网络 根据上述公式，判别网络的训练目标是最大化ℒ(, )函数，使得真实样本预测为真的概率接近于 1，生成样本预测为真的概率接近于 0。我们将判断器的误差函数实现在 d_loss_fn 函数中，将所有真实样本标注为 1，所有生成样本标注为 0，并通过最小化对应的交叉熵损失函数来实现最大化ℒ(,)函数。d_loss_fn 函数实现如下：

def d_loss_fn(generator,discriminator,batch_z,batch_x,is_training):
    #计算判别器的误差函数
    #采样生成图片
    fake_image=generator(batch_z,is_training)
    #判定生成图片
    d_fake_logits=discriminator(fake_image,is_training)
    #判定真实图片
    d_real_logits=discriminator(batch_x,is_training)
    #真实图片与1之间的误差
    d_loss_real=celoss_ones(d_real_logits)
    #生成图片与0之间的误差
    d_loss_fake=celoss_zeros(d_fake_logits)
    #合并误差
    loss=d_loss_fake+d_loss_real
    
    return loss

其中 celoss_ones 函数计算当前预测概率与标签 1 之间的交叉熵损失，代码如下：

def celoss_ones(logits):
    #计算属于与标签为1的交叉熵
    y=tf.ones_like(logits)
    loss=keras.losses.binary_crossentropy(y,logits,from_logits=True)
    return tf.reduce_mean(loss)

celoss_zeros 函数计算当前预测概率与标签 0 之间的交叉熵损失，代码如下：

def celoss_zeros(logits):
    #计算属于与便签为0的交叉熵
    y=tf.zeros_like(logits)
    loss=keras.losses.binary_crossentropy(y,logits,from_logits=True)
    return tf.reduce_men(loss)

生成网络 的训练目标是最小化ℒ(, )目标函数，由于真实样本与生成器无关，因此误差函数只需要考虑最小化${\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\cdot )}\log \left(1-D_{\theta }\left(G_{\varphi }(\mathbf{z})\right)\right)$项即可。可以通过将生成的样本标注为 1，最小化此时的交叉熵误差。需要注意的是，在反向传播误差的过程中，判别器也参与了计算图的构建，但是此阶段只需要更新生成器网络参数，而不更新判别器的网络参数。

生成器的误差函数代码如下：

def g_loss_fn(generator,discriminator,batch_z,is_training):
    # 采样生成图片
    fake_image=generator(batch_z,is_training)
    #在训练生成网络时，需要迫使生成图片判定为真
    d_fake_logits=discriminator(fake_image,is_training)
    #计算生成图片与1之间的误差
    loss=celoss_ones(d_fake_logits)

    return loss

网络训练 在每个 Epoch，首先从先验分布$p_z(\cdot )$中随机采样隐藏向量，从真实数据集中随机采样真实图片，通过生成器和判别器计算判别器网络的损失，并优化判别器网络参数。在训练生成器时，需要借助于判别器来计算误差，但是只计算生成器的梯度信息并更新。这里设定判别器训练 = 5次后，生成器训练一次。

首先创建生成网络和判别网络，并分别创建对应的优化器。代码如下：

z_dim = 100  # 隐藏向量z的长度
learning_rate = 0.0002
is_training = True
generator=Genetator()#创建生成器
generator.build(input_shape=(4,z_dim))
discriminator=Discriminator()#创建判别器
discriminator.build(input_shape=(4,64,64,3))
#分别为生成器和判别器创建优化器
g_optimizer=keras.optimizers.Adam(learning_rate=learning_rate,beta_l=0.5)
d_optimizer=keras.optimizers.Adam(learning_rate=learning_rate,beta_l=0.5)

主训练部分代码实现如下：

epochs = 3000000  # 训练步数
batch_size = 64  # batch size
for epoch in range(epochs):
    #1.训练判别器
    for _ in range(5):
        #采样隐藏向量
        batch_z=tf.random.normal([batch_size,z_dim])#[64,100]
        batch_x=next(db_iter)#采样真实图片
        #判别器前向计算
        with tf.GradientTape() as tape:
            d_loss=d_loss_fn(generator,discriminator,batch_z,batch_x,is_training)
        grads=tape.gradient(d_loss,discriminator.training_variables)
        d_optimizer.apply_gradients(zip(grads,discriminator.trainable_variables))

    #2.训练生成器
    # 采样隐藏向量
    batch_z=tf.random.normal([batch_size,z_dim])
    batch_x=next(db_iter)
    #生成器前向计算
    with tf.GradientTape() as tape:
        g_loss=g_loss_fn(generator,discriminator,batch_z,is_training)
    grads=tape.gradient(g_loss,generator.trainable_varibales)
    g_optimizer.apply_gradients(zip(grads,generator.trainable_variables))  

每间隔 100 个 Epoch，进行一次图片生成测试。通过从先验分布中随机采样隐向量，送入生成器获得生成图片，并保存为文件。

如图 13.8 所示，展示了 DCGAN 模型在训练过程中保存的生成图片样例，可以观察到，大部分图片主体明确，色彩逼真，图片多样性较丰富，图片效果较为贴近数据集中真实的图片。同时也能发现仍有少量生成图片损坏，无法通过人眼辨识图片主体。

13.4 GAN 变种

在原始的 GAN 论文中，Ian Goodfellow 从理论层面分析了 GAN 网络的收敛性，并且在多个经典图片数据集上测试了图片生成的效果，如图 13.9 所示，其中图 13.9 (a)为MNIST 数据，图 13.9 (b)为 Toronto Face 数据集，图 13.9 ©、图 13.9 (d)为 CIFAR10 数据集。

可以看到，原始 GAN 模型在图片生成效果上并不突出，和 VAE 差别不明显，此时并没有展现出它强大的分布逼近能力。但是由于 GAN 在理论方面较新颖，实现方面也有很多可以改进的地方，大大地激发了学术界的研究兴趣。在接下来的数年里，GAN 的研究如火如荼的进行，并且也取得了实质性的进展。接下来我们将介绍几个意义比较重大的 GAN变种。

13.4.1 DCGAN

最初始的 GAN 网络主要基于全连接层实现生成器 G 和判别器 D 网络，由于图片的维度较高，网络参数量巨大，训练的效果并不优秀。DCGAN提出了使用转置卷积层实现的生成网络，普通卷积层来实现的判别网络，大大地降低了网络参数量，同时图片的生成效果也大幅提升，展现了 GAN 模型在图片生成效果上超越 VAE 模型的潜质。此外，DCGAN 作者还提出了一系列经验性的 GAN 网络训练技巧，这些技巧在 WGAN 提出之前被证实有益于网络的稳定训练。前面我们已经使用 DCGAN 模型完成了二次元动漫头像的图片生成实战。

13.4.2 InfoGAN

InfoGAN 尝试使用无监督的方式去学习输入的可解释隐向量的表示方法(Interpretable Representation)，即希望隐向量能够对应到数据的语义特征。比如对于MNIST 手写数字图片，我们可以认为数字的类别、字体大小和书写风格等是图片的隐藏变量，希望模型能够学习到这些分离的(Disentangled)可解释特征表示方法，从而可以通过人为控制隐变量来生成指定内容的样本。对于 CelebA 名人照片数据集，希望模型可以把发型、眼镜佩戴情况、面部表情等特征分隔开，从而生成指定形态的人脸图片。

分离的可解释特征有什么好处呢？它可以让神经网络的可解释性更强，比如包含了一些分离的可解释特征，那么我们可以通过仅仅改变这一个位置上面的特征来获得不同语义的生成数据，如图 13.10 所示，通过将“戴眼镜男士”与“不戴眼镜男士”的隐向量相减，并与“不戴眼镜女士”的隐向量相加，可以生成“戴眼镜女士”的生成图片。

13.4.3 CycleGAN

CycleGAN是华人朱俊彦提出的无监督方式进行图片风格相互转换的算法，由于算法清晰简单，实验效果完成的较好，这项工作受到了很多的赞誉。CycleGAN 基本的假设是，如果由图片 A 转换到图片 B，再从图片 B 转换到A′，那么A′应该和 A 是同一张图片。因此除了设立标准的 GAN 损失项外，CycleGAN 还增设了循环一致性损失(CycleConsistency Loss)，来保证A′尽可能与 A 逼近。CycleGAN 图片的转换效果如图 13.11 所示。

13.4.4 WGAN

GAN 的训练问题一直被诟病，很容易出现训练不收敛和模式崩塌的现象。WGAN从理论层面分析了原始的 GAN 使用 JS 散度存在的缺陷，并提出了可以使用 Wasserstein 距离来解决这个问题。在 WGAN-GP中，作者提出了通过添加梯度惩罚项，从工程层面很好的实现了 WGAN 算法，并且实验性证实了 WGAN 训练稳定的优点。

13.4.5 Equal GAN

从 GAN 的诞生至 2017 年底，GAN Zoo 已经收集超过了 214 种 GAN 网络变种。这些 GAN 的变种或多或少地提出了一些创新，然而 Google Brain 的几位研究员在论文中提供了另一个观点：没有证据表明我们测试的 GAN 变种算法一直持续地比最初始的 GAN要好。论文中对这些 GAN 变种进行了相对公平、全面的比较，在有足够计算资源的情况下，发现几乎所有的 GAN 变种都能达到相似的性能(FID 分数)。这项工作提醒业界是否这些 GAN 变种具有本质上的创新。

13.4.6 Self-Attention GAN

Attention 机制在自然语言处理(NLP)中间已经用得非常广泛了，Self-Attention GAN(SAGAN) 借鉴了 Attention 机制，提出了基于自注意力机制的 GAN 变种。SAGAN 把图片的逼真度指标：Inception score，从最好的 36.8 提升到 52.52，Frechet Inception distance，从 27.62 降到 18.65。从图片生成效果上来看，SAGAN 取得的突破是十分显著的，同时也启发业界对自注意力机制的关注。

13.4.7 BigGAN

在 SAGAN 的基础上，BigGAN尝试将 GAN 的训练扩展到大规模上去，利用正交正则化等技巧保证训练过程的稳定性。BigGAN 的意义在于启发人们，GAN 网络的训练同样可以从大数据、大算力等方面受益。BigGAN 图片生成效果达到了前所未有的高度：Inception score 记录提升到 166.5(提高了 52.52)；Frechet Inception Distance 下降到 7.4，降低了 18.65，如图 13.13 所示，图片的分辨率可达512 × 512，图片细节极其逼真。

13.5 纳什均衡

现在我们从理论层面进行分析，通过博弈学习的训练方式，生成器 G 和判别器 D 分别会达到什么平衡状态。具体地，我们将探索以下两个问题：

❑ 固定 G，D 会收敛到什么最优状态∗?
❑ 在 D 达到最优状态∗后，G 会收敛到什么状态？

首先我们通过${\mathbf{x}}_r\sim p_r(\cdot )$一维正态分布的例子给出一个直观的解释。如图 13.14 所示，黑色虚线曲线代表了真实数据的分布$p_r(\cdot )$，为某正态分布(, 2)，绿色实线代表了生成网络学习到的分布${\mathbf{x}}_f\sim p_g(\cdot )$，蓝色虚线代表了判别器的决策边界曲线，图 13.14 (a)、(b)、( c )、(d)分别代表了生成网络的学习轨迹。

在初始状态，如图 13.14(a)所示，$p_g(\cdot )$分布与$p_r(\cdot )$差异较大，判别器可以很轻松地学习到明确的决策边界，即图 13.14(a)中的蓝色虚线，将来自$p_g(\cdot )$的采样点判定为 0，$p_r(\cdot )$中的采样点判定为 1。随着生成网络的分布$p_g(\cdot )$越来越逼近真实分布$p_r(\cdot )$，判别器越来越困难将真假样本区分开，如图 13.14(b)( c )所示。最后，生成网络学习到的分布$p_g(\cdot )$= $p_r(\cdot )$时，此时从生成网络中采样的样本非常逼真，判别器无法区分，即判定为真假样本的概率均等，如图 13.14(d)所示。

这个例子直观地解释了 GAN 网络的训练过程。

13.5.1 判别器状态

现在来推导第一个问题。回顾 GAN 的损失函数：
$$\begin{array}{rl}\mathcal{L}(G,D)& ={\int }_x{p}_r(\mathbf{x})\log (D(\mathbf{x}))d\mathbf{x}+{\int }_{\mathbf{z}}{p}_{\mathbf{z}}(\mathbf{z})\log (1-D(g(\mathbf{z})))d\mathbf{z}\\ & ={\int }_{\mathbf{x}}{p}_r(\mathbf{x})\log (D(\mathbf{x}))+p_g(\mathbf{x})\log (1-D(\mathbf{x}))d\mathbf{x}\end{array}$$

对于判别器 D，优化的目标是最大化ℒ(,)函数，需要找出函数：
$$f_{\theta }=p_r(x)\log (D(x))+p_g(x)\log (1-D(x))$$

的最大值，其中为判别器的网络参数。

我们来考虑$f_{\theta }$更通用的函数的最大值情况：
$$f(x)=A\log x+B\log (1-x)$$

要求得函数()的最大值。考虑()的导数：
$$\begin{array}{rl}& \frac{\mathrm{d}f(x)}{\mathrm{d}x}=A\frac{1}{\ln 10}\frac{1}{x}-B\frac{1}{\ln 10}\frac{1}{1-x}\\ & =\frac{1}{\ln 10}\left(\frac{A}{x}-\frac{B}{1-x}\right)\\ & =\frac{1}{\ln 10}\frac{A-(A+B)x}{x(1-x)}\end{array}$$

令$\frac{\mathrm{d}f(x)}{\mathrm{d}x}=0$，我们可以求得()函数的极值点：
$$x=\frac{A}{A+B}$$

因此，可以得知，$f_{\theta }$函数的极值点同样为：
$$D_{\theta }=\frac{p_r(\mathbf{x})}{p_r(\mathbf{x})+p_g(\mathbf{x})}$$

也就是说，判别器网络$D_{\theta }$处于$D_{{\theta }^{\ast }}$状态时，$f_{\theta }$函数取得最大值，ℒ(, )函数也取得最大值。

现在回到最大化ℒ(,)的问题，ℒ(,)的最大值点在：
$$D^{\ast }=\frac{A}{A+B}=\frac{p_r(x)}{p_r(x)+p_g(x)}$$
时取得，此时也是的最优状态∗。

13.5.2 生成器状态

在推导第二个问题之前，我们先介绍一下与 KL 散度类似的另一个分布距离度量标准：JS 散度，它定义为 KL 散度的组合：
$$\begin{array}{c}{D}_{KL}(p\Vert q)={\int }_{x}p(x)\log \frac{p(x)}{q(x)}dx\\ D_{JS}(p\Vert q)=\frac{1}{2}{D}_{KL}\left(p\Vert \frac{p+q}{2}\right)+\frac{1}{2}{D}_{KL}\left(q\Vert \frac{p+q}{2}\right)\end{array}$$

JS 散度克服了 KL 散度不对称的缺陷。

当 D 达到最优状态∗时，我们来考虑此时$p_r$和$p_g$的 JS 散度：
$$D_{JS}\left(p_r\Vert p_g\right)=\frac{1}{2}{D}_{KL}\left(p_r\Vert \frac{p_r+p_g}{2}\right)+\frac{1}{2}{D}_{KL}\left(p_g\Vert \frac{p_r+p_g}{2}\right)$$
根据 KL 散度的定义展开为：
$$\begin{array}{rl}{D}_{JS}\left(p_r||p_g\right)& =\frac{1}{2}\left(\log 2+{\int }_x{p}_r(x)\log \frac{p_r(x)}{p_r+p_g(x)}dx\right)\\ & +\frac{1}{2}\left(\log 2+{\int }_x{p}_g(x)\log \frac{p_g(x)}{p_r+p_g(x)}dx\right)\end{array}$$
合并常数项可得：
$$D_{JS}\left(p_r\Vert p_g\right)=\frac{1}{2}(\log 2+\log 2)$$
$$+\frac{1}{2}\left({\int }_x{p}_r(x)\log \frac{p_r(x)}{p_r+p_g(x)}dx+{\int }_x{p}_g(x)\log \frac{p_g(x)}{p_r+p_g(x)}dx\right)$$
即：
$$\begin{array}{c}{D}_{JS}\left(p_r||p_g\right)=\frac{1}{2}(\log 4)\\ +\frac{1}{2}\left({\int }_x{p}_r(x)\log \frac{p_r(x)}{p_r+p_g(x)}dx+{\int }_x{p}_g(x)\log \frac{p_g(x)}{p_r+p_g(x)}dx\right)\end{array}$$

考虑在判别网络到达∗时，此时的损失函数为：
$$\begin{array}{l}\mathcal{L}\left(G,D^{\ast }\right)={\int }_x{p}_r(\mathbf{x})\log \left(D^{\ast }(\mathbf{x})\right)+p_g(\mathbf{x})\log \left(1-D^{\ast }(\mathbf{x})\right)d\mathbf{x}\\ ={\int }_{\mathbf{x}}{p}_r(\mathbf{x})\log \frac{p_r(\mathbf{x})}{p_r+p_g(\mathbf{x})}d\mathbf{x}+{\int }_{\mathbf{x}}{p}_g(\mathbf{x})\log \frac{p_g(\mathbf{x})}{p_r+p_g(\mathbf{x})}d\mathbf{x}\end{array}$$
因此在判别网络到达∗时，$D_{JS}\left(p_r\Vert p_g\right)$与$\mathcal{L}\left(G,D^{\ast }\right)$满足关系：
$$D_{JS}\left(p_r\Vert p_g\right)=\frac{1}{2}\left(\log 4+\mathcal{L}\left(G,D^{\ast }\right)\right)$$
即：
$$\mathcal{L}\left(G,D^{\ast }\right)=2D_{JS}\left(p_r\Vert p_g\right)-2\log 2$$
对于生成网络 G 而言，训练目标是${\min }_G\mathcal{L}(G,D)$ ，考虑到 JS 散度具有性质：
$$D_{JS}\left(p_r\Vert p_g\right)\ge 0$$
因此$\mathcal{L}\left(G,D^{\ast }\right)$取得最小值仅在$D_{JS}\left(p_r\Vert p_g\right)=0$时(此时$p_g$=$p_r$)，$\mathcal{L}\left(G,D^{\ast }\right)$取得最小值：
$$\mathcal{L}\left(G^{\ast },D^{\ast }\right)=-2\log 2$$
此时生成网络∗的状态是：
$$p_g=p_r$$
即∗的学到的分布$p_g$与真实分布$p_r$一致，网络达到平衡点，此时：
$$D^{\ast }=\frac{p_r(\mathbf{x})}{p_r(\mathbf{x})+p_g(\mathbf{x})}=0.5$$

13.5.3 纳什均衡点

通过上面的推导，我们可以总结出生成网络 G 最终将收敛到真实分布，即：
$$p_g=p_r$$
此时生成的样本与真实样本来自同一分布，真假难辨，在判别器中均有相同的概率判定为
真或假，即
$$D(\cdot )=0.5$$
此时损失函数为
$$\mathcal{L}\left(G^{\ast },D^{\ast }\right)=-2\log 2$$

13.6 GAN 训练难题

尽管从理论层面分析了 GAN 网络能够学习到数据的真实分布，但是在工程实现中，常常出现 GAN 网络训练困难的问题，主要体现在 GAN 模型对超参数较为敏感，需要精心挑选能使模型工作的超参数设定，同时也容易出现模式崩塌现象。

13.6.1 超参数敏感

超参数敏感是指网络的结构设定、学习率、初始化状态等超参数对网络的训练过程影响较大，微量的超参数调整将可能导致网络的训练结果截然不同。如图 13.15 所示，图(a)为 GAN 模型良好训练得到的生成样本，图(b)中的网络由于没有采用 Batch Normalization层等设置，导致 GAN 网络训练不稳定，无法收敛，生成的样本与真实样本差距非常大。

为了能较好地训练 GAN 网络，DCGAN 论文作者提出了不使用 Pooling 层、多使用Batch Normalization 层、不使用全连接层、生成网络中激活函数应使用 ReLU、最后一层使用tanh激活函数、判别网络激活函数应使用 LeakyLeLU 等一系列经验性的训练技巧。但是这些技巧仅能在一定程度上避免出现训练不稳定的现象，并没有从理论层面解释为什么会出现训练困难、以及如果解决训练不稳定的问题。

13.6.2 模式崩塌

模式崩塌(Mode Collapse)是指模型生成的样本单一，多样性很差的现象。由于判别器只能鉴别单个样本是否采样自真实分布，并没有对样本多样性进行显式约束，导致生成模型可能倾向于生成真实分布的部分区间中的少量高质量样本，以此来在判别器中获得较高的概率值，而不会学习到全部的真实分布。模式崩塌现象在 GAN 中比较常见，如图 13.16所示，在训练过程中，通过可视化生成网络的样本可以观察到，生成的图片种类非常单一，生成网络总是倾向于生成某种单一风格的样本图片，以此骗过判别器。

另一个直观地理解模式崩塌的例子如图 13.17 所示，第一行为未出现模式崩塌现象的生成网络的训练过程，最后一列为真实分布，即 2D 高斯混合模型；第二行为出现模式崩塌现象的生成网络的训练过程，最后一列为真实分布。可以看到真实的分布由 8 个高斯模型混合而成，出现模式崩塌后，生成网络总是倾向于逼近真实分布的某个狭窄区间，如图13.17 第 2 行前 6 列所示，从此区间采样的样本往往能够在判别器中较大概率判断为真实样本，从而骗过判别器。但是这种现象并不是我们希望看到的，我们希望生成网络能够逼近真实的分布，而不是真实分布中的某部分。

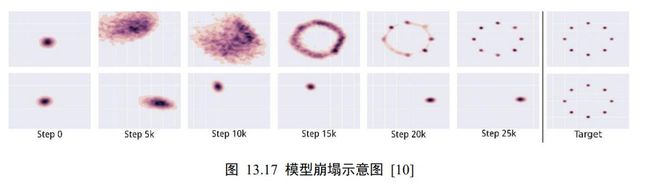
那么怎么解决 GAN 训练的难题，让 GAN 可以像普通的神经网络一样训练较为稳定呢？WGAN 模型给出了一种解决方案。

13.7 WGAN 原理

WGAN 算法从理论层面分析了 GAN 训练不稳定的原因，并提出了有效的解决方法。那么是什么原因导致了 GAN 训练如此不稳定呢？WGAN 提出是因为 JS 散度在不重叠的分布和上的梯度曲面是恒定为 0 的。如图 13.19 所示，当分布和不重叠时，JS 散度的梯度值始终为 0，从而导致此时 GAN 的训练出现梯度弥散现象，参数长时间得不到更新，网络无法收敛。

接下来我们将详细阐述 JS 散度的缺陷以及怎么解决此缺陷。

13.7.1 JS 散度的缺陷

为了避免过多的理论推导，我们这里通过一个简单的分布实例来解释 JS 散度的缺陷。考虑完全不重叠( ≠ 0)的两个分布和，其中分布为：
$$\forall (x,y)\in p,x=0,y\sim \mathrm{U}(0,1)$$
分布为：
$$\forall (x,y)\in q,x=\theta ,y\sim \mathrm{U}(0,1)$$
其中 ∈ ，当 = 0时，分布和重叠，两者相等；当 ≠ 0时，分布和不重叠。

我们来分析上述分布和之间的 JS 散度随的变化情况。根据 KL 散度与 JS 散度的定义，计算 = 0时的 JS 散度(||)：
$$D_{KL}(p\Vert q)=\sum _{x=0,y\sim U(0,1)}1\cdot \log \frac{1}{0}=+\infty$$
$$D_{KL}(q\Vert p)=\sum _{x=\theta ,y\sim \mathrm{U}(0,1)}1\cdot \log \frac{1}{0}=+\infty$$
$$D_{JS}(p\Vert q)=\frac{1}{2}\left(\sum _{x=0,y\sim U(0,1)}1\cdot \log \frac{1}{1/2}+\sum _{x=0,y\sim U(0,1)}1\cdot \log \frac{1}{1/2}\right)=\log 2$$
当 = 0时，两个分布完全重叠，此时的 JS 散度和 KL 散度都取得最小值，即 0：
$$D_{KL}(p\Vert q)=D_{KL}(q\Vert p)=D_{JS}(p\Vert q)=0$$
从上面的推导，我们可以得到$|D_{JS}(p\Vert q)$随的变化趋势：
$$D_{JS}(p\Vert q)=\{\begin{array}{cl}\log 2& \theta \ne 0\\ 0& \theta =0\end{array}$$
也就是说，当两个分布完全不重叠时，无论分布之间的距离远近，JS 散度为恒定值log 2，此时 JS 散度将无法产生有效的梯度信息；当两个分布出现重叠时，JS 散度才会平滑变动，产生有效梯度信息；当完全重合后，JS 散度取得最小值 0。如图 13.19 中所示，红色的曲线分割两个正态分布，由于两个分布没有重叠，生成样本位置处的梯度值始终为 0，无法更新生成网络的参数，从而出现网络训练困难的现象。

因此，JS 散度在分布和不重叠时是无法平滑地衡量分布之间的距离，从而导致此位置上无法产生有效梯度信息，出现 GAN 训练不稳定的情况。要解决此问题，需要使用一种更好的分布距离衡量标准，使得它即使在分布和不重叠时，也能平滑反映分布之间的真实距离变化。

13.7.2 EM 距离

WGAN 论文发现了 JS 散度导致 GAN 训练不稳定的问题，并引入了一种新的分布距离度量方法：Wasserstein 距离，也叫推土机距离(Earth-Mover Distance，简称 EM 距离)，它表示了从一个分布变换到另一个分布的最小代价，定义为：
$$W(p,q)=\underset{\gamma \sim \Pi (p,q)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$$
其中∏(, )是分布和组合起来的所有可能的联合分布的集合，对于每个可能的联合分布 ∼ ∏(, )，计算距离‖ − ‖的期望(,)∼[‖ − ‖]，其中(, )采样自联合分布。不同的联合分布有不同的期望(,)∼[‖ − ‖]，这些期望中的下确界即定义为分布和的Wasserstein 距离。其中inf{∙}表示集合的下确界，例如{|1 < < 3, ∈ }的下确界为 1。

继续考虑图 13.18 中的例子，我们直接给出分布和之间的 EM 距离的表达式：
$$W(p,q)=|\theta |$$
绘制出 JS 散度和 EM 距离的曲线，如图 13.20 所示，可以看到，JS 散度在 = 0处不连续，其他位置导数均为 0，而 EM 距离总能够产生有效的导数信息，因此 EM 距离相对于JS 散度更适合指导 GAN 网络的训练。

13.7.3 WGAN-GP

考虑到几乎不可能遍历所有的联合分布去计算距离‖ − ‖的期望(,)∼[‖ − ‖]，因此直接计算生成网络分布$p_g$与真实数据分布$p_r$的$W\left(p_r,p_g\right)$距离是不现实的，WGAN 作者基于 Kantorovich-Rubinstein 对偶性将直接求$W\left(p_r,p_g\right)$转换为求：
$$W\left(p_r,p_g\right)=\frac{1}{K}\underset{\Vert f{\Vert }_L\le K}{\sup }{\mathbb{E}}_{x\sim p_r}[f(x)]-{\mathbb{E}}_{x\sim p_g}[f(x)]$$
其中{∙}表示集合的上确界，|||| ≤ 表示函数: → 满足 K-阶 Lipschitz 连续性，即满足
$$\left|f\left(x_1\right)-f\left(x_2\right)\right|\le K\cdot \left|x_1-x_2\right|$$
于是，我们使用判别网络$D_{\theta }(x)$参数化()函数，在$D_{\theta }$满足 1 阶-Lipschitz 约束的条件下，即 = 1，此时：
$$W\left(p_r,p_g\right)=\underset{{\Vert D_{\theta }\Vert }_L\le 1}{\sup }{\mathbb{E}}_{x\sim p_r}\left[D_{\theta }(\mathbf{x})\right]-{\mathbb{E}}_{\mathbf{x}\sim p_g}\left[D_{\theta }(\mathbf{x})\right]$$
因此求解$W\left(p_r,p_g\right)$的问题可以转化为：
$$\underset{\theta }{\max }{\mathbb{E}}_{x\sim p_r}\left[D_{\theta }(\mathbf{x})\right]-{\mathbb{E}}_{\mathbf{x}\sim p_g}\left[D_{\theta }(\mathbf{x})\right]$$
这就是判别器 D的优化目标。判别网络函数$D_{\theta }(x)$需要满足 1 阶-Lipschitz 约束：
$${\nabla }_{x}D(\hat{\mathbf{x}})\le I$$
在 WGAN-GP 论文中，作者提出采用增加梯度惩罚项(Gradient Penalty)方法来迫使判别网络满足 1 阶-Lipschitz 函数约束，同时作者发现将梯度值约束在 1 周围时工程效果更好，因此梯度惩罚项定义为：
$$\mathrm{G}\mathrm{P}\triangleq {\mathbb{E}}_{\hat{x}\sim P_{\hat{x}}}\left[{\left({\Vert {\nabla }_{\hat{x}}D(\hat{x})\Vert }_2-1\right)}^2\right]$$
因此 WGAN 的判别器 D 的训练目标为：
$$\underset{\theta }{\max }\mathcal{L}(G,D)=\underset{EM{\mathcal{L}}_{\mathbb{R}}}{{\mathbb{E}}_{x_r\sim p_r}\left[D\left({\mathbf{x}}_r\right)\right]-{\mathbb{E}}_{x_f\sim p_g}\left[D\left({\mathbf{x}}_f\right)\right]}\underset{GP\mathbb{Z},\mathbb{U}\mathcal{H}}{-\lambda {\mathbb{E}}_{{\hat{\mathbf{x}}}_{{\mathcal{P}}_{\tilde{\mathbf{x}}}}}\left[{\left({\Vert {\nabla }_{\hat{\mathbf{x}}}D(\hat{\mathbf{x}})\Vert }_2-1\right)}^2\right]}$$
其中̂来自于与的线性差值：
$$\hat{x}=t{\mathbf{x}}_r+(1-t){\mathbf{x}}_f,t\in [0,1]$$
判别器 D 的目标是最小化上述的误差ℒ(,)，即迫使生成器 G 的分布$p_g$与真实分布$p_r$之间 EM 距离${\mathbb{E}}_{x_r\sim p_r}\left[D\left({\mathbf{x}}_r\right)\right]-{\mathbb{E}}_{{\mathbf{x}}_f\sim p_g}\left[D\left({\mathbf{x}}_f\right)\right]$项尽可能大,${\Vert {\nabla }_{x}D(\mathbf{x})\Vert }_2$逼近于 1。

WGAN 的生成器 G 的训练目标为：
$$\underset{\varphi }{\min }\mathcal{L}(G,D)=\underset{EM{\mathbb{E}}_{\mathbb{E}}}{{\mathbb{E}}_{x_r\sim p_r}\left[D\left({\mathbf{x}}_r\right)\right]-{\mathbb{E}}_{{\mathbf{x}}_f\sim p_g}\left[D\left({\mathbf{x}}_f\right)\right]}$$

即使得生成器的分布$p_g$与真实分布$p_r$之间的 EM 距离越小越好。考虑到${\mathbb{E}}_{x_r\sim p_r}\left[D\left({\mathbf{x}}_r\right)\right]$一项与生成器无关，因此生成器的训练目标简写为：
$$\begin{array}{c}{\min }_{\varphi }\mathcal{L}(G,D)=-{\mathbb{E}}_{x_f\sim p_g}\left[D\left(x_f\right)\right]\\ =-{\mathbb{E}}_{z\sim p_z(\cdot )}[D(G(z))]\end{array}$$
从实现来看，判别网络 D 的输出不需要添加 Sigmoid 激活函数，这是因为原始版本的判别器的功能是作为二分类网络，添加 Sigmoid 函数获得类别的概率；而 WGAN 中判别器作为 EM 距离的度量网络，其目标是衡量生成网络的分布和真实分布之间的 EM 距离，属于实数空间，因此不需要添加 Sigmoid 激活函数。在误差函数计算时，WGAN 也没有 log 函数存在。在训练 WGAN 时，WGAN 作者推荐使用 RMSProp 或 SGD 等不带动量的优化器。

WGAN 从理论层面发现了原始 GAN 容易出现训练不稳定的原因，并给出了一种新的距离度量标准和工程实现解决方案，取得了较好的效果。WGAN 还在一定程度上缓解了模式崩塌的问题，使用 WGAN 的模型不容易出现模式崩塌的现象。需要注意的是，WGAN一般并不能提升模型的生成效果，仅仅是保证了模型训练的稳定性。当然，保证模型能够稳定地训练也是取得良好效果的前提。如图13.21 所示，原始版本的 DCGAN 在不使用BN 层等设定时出现了训练不稳定的现象，在同样设定下，使用 WGAN 来训练判别器可以避免此现象，如图 13.22 所示。

13.8 WGAN-GP 实战

WGAN-GP 模型可以在原来 GAN 代码实现的基础上仅做少量修改。WGAN-GP 模型的判别器 D 的输出不再是样本类别的概率，输出不需要加 Sigmoid 激活函数。同时添加梯度惩罚项，实现如下：

def gradient_penalty(discriminator, batch_x, fake_image):
    # 梯度惩罚项计算函数
    batchsz = batch_x.shape[0]
    # 每个样本均随机采样 t,用于插值
    t = tf.random.uniform([batchsz, 1, 1, 1])
    # 自动扩展为 x 的形状，[b, 1, 1, 1] => [b, h, w, c]
    t = tf.broadcast_to(t, batch_x.shape)
    # 在真假图片之间做线性插值
    interplate = t * batch_x + (1 - t) * fake_image
   # 在梯度环境中计算 D 对插值样本的梯度
   with tf.GradientTape() as tape:
       tape.watch([interplate]) # 加入梯度观察列表
       d_interplote_logits = discriminator(interplate)
   grads = tape.gradient(d_interplote_logits, interplate)
   # 计算每个样本的梯度的范数:[b, h, w, c] => [b, -1]
   grads = tf.reshape(grads, [grads.shape[0], -1])
   gp = tf.norm(grads, axis=1) #[b]
   # 计算梯度惩罚项
   gp = tf.reduce_mean( (gp-1.)**2 )
   return gp

WGAN 判别器的损失函数计算与 GAN 不一样，WGAN 是直接最大化真实样本的输出值，最小化生成样本的输出值，并没有交叉熵计算的过程。代码实现如下：

def d_loss_fn(generator, discriminator, batch_z, batch_x, is_training):
    # 计算 D 的损失函数
    fake_image = generator(batch_z, is_training) # 假样本
    d_fake_logits = discriminator(fake_image, is_training) # 假样本的输出
    d_real_logits = discriminator(batch_x, is_training) # 真样本的输出
    # 计算梯度惩罚项
    gp = gradient_penalty(discriminator, batch_x, fake_image)
    # WGAN-GP D 损失函数的定义，这里并不是计算交叉熵，而是直接最大化正样本的输出
    # 最小化假样本的输出和梯度惩罚项
    loss = tf.reduce_mean(d_fake_logits) - tf.reduce_mean(d_real_logits) + 10. * gp
    return loss, gp

WGAN 生成器 G 的损失函数是只需要最大化生成样本在判别器 D 的输出值即可，同样没有交叉熵的计算步骤。代码实现如下：

def g_loss_fn(generator, discriminator, batch_z, is_training):
   # 生成器的损失函数
   fake_image = generator(batch_z, is_training)
   d_fake_logits = discriminator(fake_image, is_training)
   # WGAN-GP G 损失函数，最大化假样本的输出值
   loss = - tf.reduce_mean(d_fake_logits)
   return loss

WGAN 的主训练逻辑基本相同，与原始的 GAN 相比，判别器 D 的作用是作为一个EM 距离的计量器存在，因此判别器越准确，对生成器越有利，可以在训练一个 Step 时训练判别器 D 多次，训练生成器 G 一次，从而获得较为精准的 EM 距离估计。

参考文献

1.https://github.com/chenyuntc/pytorch-book
2.那么多GAN哪个好？谷歌大脑泼来冷水：都和原版差不多 | 论文