阿里天池新人赛——二手车价格预测（特征工程）

特征工程

引入

数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限。

特征工程目的

最大限度地从原始数据中提取特征以供算法和模型使用，因为高质量的特征有助于提高模型整体的性能和准确性，所以特征工程在整个项目中有着举足轻重的位置。

内容

• 数据预处理
  1. 异常处理
     箱线图分析删除异常值、BOX-COX转换（处理有偏）、长尾截断。
  2. 特征的归一化/标准化
     数据标准化和归一化、针对幂律分布，采用公式$log(\frac{1+x}{1+median})$
  3. 缺失值处理
     等频分桶、等距分桶、Best-KS分桶、卡方分布
  4. 缺失值处理：
     不处理（类似XGBoost树模型）、删除、补全、分箱
• 特征构造
  1. 构造统计量特征，如count、sum、std等等
  2. 时间特征，如相对时间和绝对时间，节假日等
  3. 地理信息，如分箱、分布编码等
  4. 非线性变换，如log、平方、根号等
  5. 特征组合、特征交叉
  6. 灵活处理
• 特征筛选
  1. 过滤式(filter)
  2. 包裹式（wrapper）
  3. 嵌入式
• 降维
  1. PCA/LDA/LCA;
  2. 特征选择也是一种降维

实现代码

归一化、标准化

归一化和标准化详见
特征缩放是数据要做的最重要的转换之一。除了个别情况，当输入的数值属性量度不同，不同的特征指标有的不一样的量度和单位，这样就会影响到数据分析的结果，以至于机器学习算法的性能都不会好，此时就需要对数据进行归一化或标准化的处理。

• 归一化：将数据缩放到区间[0,1]
  $$X^{\prime }=\frac{x-x_{min}}{x_{max}-x_{min}}$$

from sklearn import preprocessing
import numpy as np
x = np.array([[10,2,3],
              [4,5,6],
              [7,8,9]])
##对每一列进行归一化
min_max_scaler = preprocessing.MinMaxScaler()
x_minmax = min_max_scaler.fit_transform(x)
print(x_minmax)
#[[1.  0.  0. ]
# [0.  0.5 0.5]
#[0.5 1.  1. ]]

• 标准化：去除数据的单位限制，将其转化为无量纲的纯数值，通过对原始数据进行变换把数据变换到均值为0,方差为1范围内。
  $$X^{\prime }=\frac{x-mean}{\sigma }$$

from sklearn.preprocessing import StandardScaler
std = StandardScaler()
data = std.fit_transform([[1., -1., 3.],
                          [2., 4., 2.],
                          [4., 6., -1.]])
print(data)
#[[-1.06904497 -1.35873244  0.98058068]
# [-0.26726124  0.33968311  0.39223227]
# [ 1.33630621  1.01904933 -1.37281295]]

导入基础数据科学库和绘图库

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from operator import itemgetter
%matplotlib inline

operator.itemgetter函数
operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为一些序号（即需要获取的数据在对象中的序号)
例子：

a = [1,2,3] 
b=operator.itemgetter(1)//定义函数b，获取对象的第1个域的值
print(b(a))
## 输出 ：  2

获取数据并总览数据

Train_data=pd.read_csv('./used_car_train_20200313/used_car_train_20200313.csv',sep=' ')
Test_data=pd.read_csv('./used_car_testA_20200313/used_car_testA_20200313.csv',sep=' ')
#数据集大小
print(Train_data.shape)
print(Test_data.shape)
#数据集列名、数量、数值类型
print(Train_data.info())
print(Test_data.info())

异常处理

箱线图删除异常值：
使用箱线图，加入一个参数scale，调整我们删除异常值时的一个阈值，即调整箱线图中上限下限，超过或者低于这个阈值时，则删除。

# 这里我包装了一个异常值处理的代码，可以随便调用。
def outliers_proc(data, col_name, scale=3):
    """
    用于清洗异常值，默认用 box_plot（scale=3）进行清洗
    :param data: 接收 pandas 数据格式
    :param col_name: pandas 列名
    :param scale: 尺度
    :return:
    """

    def box_plot_outliers(data_ser, box_scale):
        """
        利用箱线图去除异常值
        :param data_ser: 接收 pandas.Series 数据格式
        :param box_scale: 箱线图尺度，
        :return:
        """
        iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
        val_low = data_ser.quantile(0.25) - iqr
        val_up = data_ser.quantile(0.75) + iqr
        rule_low = (data_ser < val_low)
        rule_up = (data_ser > val_up)
        return (rule_low, rule_up), (val_low, val_up)

    data_n = data.copy()
    data_series = data_n[col_name]
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
    print("Delete number is: {}".format(len(index)))
    data_n = data_n.drop(index)
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: {}".format(data_n.shape[0]))
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())
    
    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n
#我们可以删除一些异常数据，以power为例，
#test数据不能删，test数据是要去预测的
Train_data=outliers_proc(Train_data,'power',scale=3)

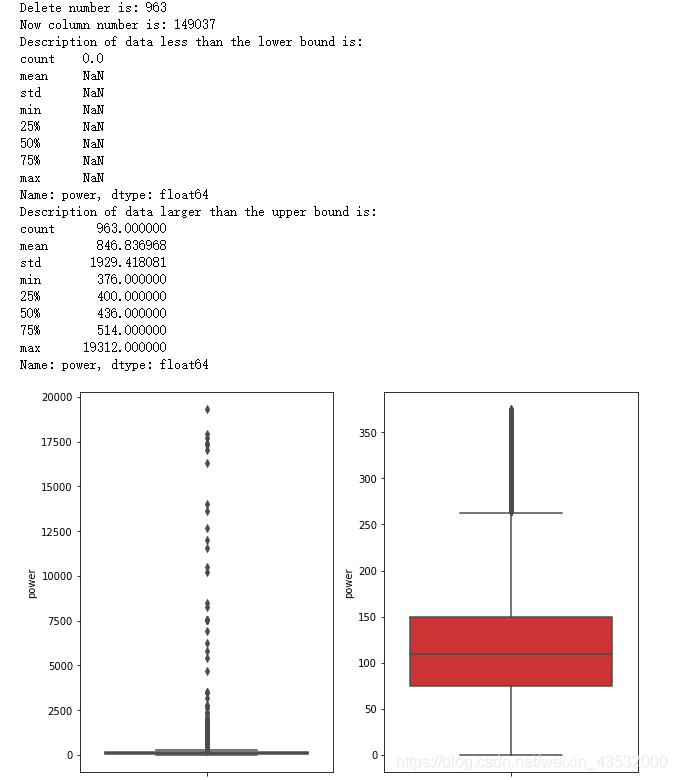
box-cox变换（处理有偏分布）：
在数据预处理时，对某些特征做$Y=log(1+X)$的操作，可以将特征分布正态化,使数据更符合后面的数据挖掘对数据分布的假设。
Box-Cox变换：$Y=log(1+x)$用来降低特征的Skewness，即处理特征有偏分布，从而达到接近正态分布和稳定的方差。

特征构造

特征构造意味着从现有的数据中构造额外特征

# 训练集和测试集放在一起，方便构造特征
Train_data['train']=1
Test_data['train']=0
data = pd.concat([Train_data, Test_data], ignore_index=True)

根据特征’creatDate’和‘regDate’构建新特征车辆的使用时间‘used_time’

# 使用时间：data['creatDate'] - data['regDate']，反应汽车使用时间，一般来说价格与使用时间成反比
# 不过要注意，数据里有时间出错的格式，所以我们需要 errors='coerce'
data['used_time'] = (pd.to_datetime(data['creatDate'], format='%Y%m%d', errors='coerce') - 
                            pd.to_datetime(data['regDate'], format='%Y%m%d', errors='coerce')).dt.days

# 看一下空数据，有 15k 个样本的时间是有问题的，我们可以选择删除，也可以选择放着。
# 但是这里不建议删除，因为删除缺失数据占总样本量过大，7.5%
# 我们可以先放着，因为如果我们 XGBoost 之类的决策树，其本身就能处理缺失值，所以可以不用管；
data['used_time'].isnull().sum()
#15072

由邮政编码中提取出新的特征:城市

# 从邮编中提取城市信息，相当于加入了先验知识
data['city'] = data['regionCode'].apply(lambda x : str(x)[:-3])
data = data

构造统计量特征

# 计算某品牌的销售统计量，还可以计算其他特征的统计量
# 这里要以 train 的数据计算统计量
Train_gb = Train_data.groupby("brand")
all_info = {}
for kind, kind_data in Train_gb:
    info = {}
    kind_data = kind_data[kind_data['price'] > 0]
    info['brand_amount'] = len(kind_data)
    info['brand_price_max'] = kind_data.price.max()
    info['brand_price_median'] = kind_data.price.median()
    info['brand_price_min'] = kind_data.price.min()
    info['brand_price_sum'] = kind_data.price.sum()
    info['brand_price_std'] = kind_data.price.std()
    info['brand_price_average'] = round(kind_data.price.sum() / (len(kind_data) + 1), 2)
    all_info[kind] = info
brand_fe = pd.DataFrame(all_info).T.reset_index().rename(columns={"index": "brand"})
data = data.merge(brand_fe, how='left', on='brand')

数据分箱：
建立分类模型时，需要对连续变量离散化，特征离散化后，模型会更稳定，降低了模型过拟合的风险。比如在建立申请评分卡模型时用logsitic作为基模型就需要对连续变量进行离散化，离散化通常采用分箱法。
例如：将年龄划分区间：(0-18)未成年、（18-50）、等等。

# 数据分桶 以 power 为例
# 这时候我们的缺失值也进桶了，
# 为什么要做数据分箱呢，原因有很多，= =
# 1. 离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
# 2. 离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；
# 3. LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
# 4. 离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；
# 5. 特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化

# 当然还有很多原因，LightGBM 在改进 XGBoost 时就增加了数据分桶，增强了模型的泛化性

bin = [i*10 for i in range(31)]
data['power_bin'] = pd.cut(data['power'], bin, labels=False)
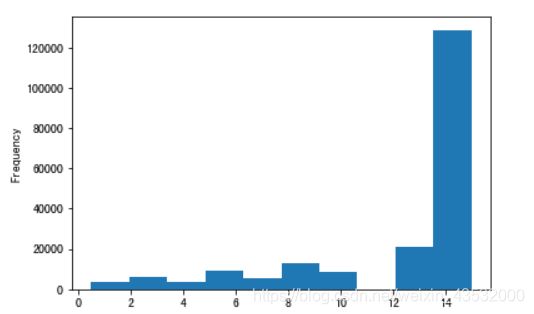
data[['power_bin', 'power']].head()

# 删除不需要的数据
data = data.drop(['creatDate', 'regDate', 'regionCode'], axis=1)
# 目前的数据其实已经可以给树模型使用了，所以我们导出一下
data.to_csv('data_for_tree.csv', index=0)

由于不同模型对数据集的要求不同，因此我们可以再构造一份数据给LR NN之类的模型使用。
Tree Mode l不需要对特征进行归一化 不太需要 one-hot 编码

# 我们看下数据分布：
data['power'].plot.hist()

# 我们刚刚已经对 train 进行异常值处理了，但是现在还有这么奇怪的分布是因为 test 中的 power 异常值，
# 所以我们其实刚刚 train 中的 power 异常值不删为好，可以用长尾分布截断来代替
Train_data['power'].plot.hist()

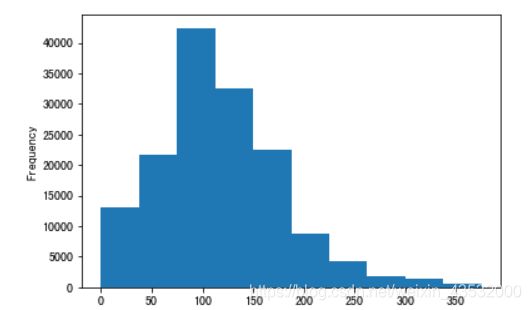
对其取log的原因，因为data[‘power’]是有偏分布

# 我们对其取 log，在做归一化
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
data['power'] = np.log(data['power'] + 1) 
data['power'] = ((data['power'] - np.min(data['power'])) / (np.max(data['power']) - np.min(data['power'])))
data['power'].plot.hist()

# km 的比较正常，应该是已经做过分桶了
data['kilometer'].plot.hist()

直接归一化

data['kilometer'] = ((data['kilometer'] - np.min(data['kilometer'])) / 
                        (np.max(data['kilometer']) - np.min(data['kilometer'])))
# 除此之外 还有我们刚刚构造的统计量特征：
# 'brand_amount', 'brand_price_average', 'brand_price_max',
# 'brand_price_median', 'brand_price_min', 'brand_price_std',
# 'brand_price_sum'
# 这里不再一一举例分析了，直接做变换，
def max_min(x):
    return (x - np.min(x)) / (np.max(x) - np.min(x))

data['brand_amount'] = ((data['brand_amount'] - np.min(data['brand_amount'])) / 
                        (np.max(data['brand_amount']) - np.min(data['brand_amount'])))
data['brand_price_average'] = ((data['brand_price_average'] - np.min(data['brand_price_average'])) / 
                               (np.max(data['brand_price_average']) - np.min(data['brand_price_average'])))
data['brand_price_max'] = ((data['brand_price_max'] - np.min(data['brand_price_max'])) / 
                           (np.max(data['brand_price_max']) - np.min(data['brand_price_max'])))
data['brand_price_median'] = ((data['brand_price_median'] - np.min(data['brand_price_median'])) /
                              (np.max(data['brand_price_median']) - np.min(data['brand_price_median'])))
data['brand_price_min'] = ((data['brand_price_min'] - np.min(data['brand_price_min'])) / 
                           (np.max(data['brand_price_min']) - np.min(data['brand_price_min'])))
data['brand_price_std'] = ((data['brand_price_std'] - np.min(data['brand_price_std'])) / 
                           (np.max(data['brand_price_std']) - np.min(data['brand_price_std'])))
data['brand_price_sum'] = ((data['brand_price_sum'] - np.min(data['brand_price_sum'])) / 
                           (np.max(data['brand_price_sum']) - np.min(data['brand_price_sum'])))

对类别特征进行one-hot

# 对类别特征进行 OneEncoder
data = pd.get_dummies(data, columns=['model', 'brand', 'bodyType', 'fuelType',
                                     'gearbox', 'notRepairedDamage', 'power_bin'])
 # 这份数据可以给 LR 用
data.to_csv('data_for_lr.csv', index=0)
                                     

特征筛选

过滤式
按照某种规则对数据集进行特征选择，然后再训练学习器，特征选择过程与后续学习器无关，这相当于先用特征选择过程对初始特征进行“过滤”，再用过滤后的特征来训练模型
方差选择、相关系数法、卡方检验法

# 相关性分析
print(data['power'].corr(data['price'], method='spearman'))
print(data['kilometer'].corr(data['price'], method='spearman'))
print(data['brand_amount'].corr(data['price'], method='spearman'))
print(data['brand_price_average'].corr(data['price'], method='spearman'))
print(data['brand_price_max'].corr(data['price'], method='spearman'))
print(data['brand_price_median'].corr(data['price'], method='spearman'))
#0.572828519605
#-0.408256970162
#0.0581566100256
#0.383490957606
#0.259066833881
#0.386910423934

# 当然也可以直接看图
data_numeric = data[['power', 'kilometer', 'brand_amount', 'brand_price_average', 
                     'brand_price_max', 'brand_price_median']]
correlation = data_numeric.corr()

f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True,  vmax=0.8)

包裹式
从初始特征集合中不断的选择特征子集，训练学习器，根据学习器的性能来对子集进行评价，直到选择出最佳的子集

# k_feature 太大会很难跑，没服务器，所以提前 interrupt 了
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.linear_model import LinearRegression
sfs = SFS(LinearRegression(),
           k_features=10,
           forward=True,
           floating=False,
           scoring = 'r2',
           cv = 0)
x = data.drop(['price'], axis=1)
x = x.fillna(0)
y = data['price']
sfs.fit(x, y)
sfs.k_feature_names_ 

# 画出来，可以看到边际效益
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
import matplotlib.pyplot as plt
fig1 = plot_sfs(sfs.get_metric_dict(), kind='std_dev')
plt.grid()
plt.show()

嵌入式
嵌入式特征选择是将特征选择过程与学习器训练过程融为一体，两者在同一个优化过程中完成，即在学习器训练过程中自动地进行了特征选择。