【论文阅读】【综述】从Optical Flow到Scene Flow
文章目录
- Optical Flow
- FlowNet(2015ICCV)
- FlowNet2.0(2017CVPR)
- PWCNet(2018CVPR)
- MaskFlowNet(2020CVPR)
- Sene Flow
- Point-based
- PointFlowNet(2019CVPR)
- FlowNet3D(2019CVPR)
- FlowNet3D++(2020WACV)
- HPLFlowNet(2019CVPR)
- PointPWC-Net(2019arxiv)
- Just Go with the Flow(2020CVPR)
- Voxel-based
- MotionNet (2020CVPR)
Scene Flow可以理解为3D的光流,数据换成了点云,Flow是用xyz三个坐标表示。与目标检测相似,想要了解Scene Flow的发展,就得先了解Optical Flow的方法。我也是刚刚开始看这个领域,所以总结的不到位,欢迎各位看官批评指正。
我的关注点在于Scene Flow,所以Optical Flow的很多方法就没有放上来。只是放了一些对Scene Flow有启发的文章。
Optical Flow
FlowNet(2015ICCV)
早期的代表性方法,2015年resnet才被提出来。
该方法提出了两个网络,分别是FlowNetC和FlowNetS,如下图所示。
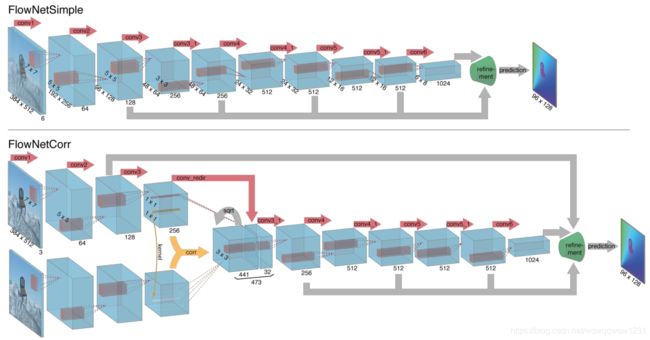
FlowNetS非常简单,就是把两张图片堆叠在一起,然后用分割的网络去预测。
FlowNetC则复杂一些,提出了两个feature map的correlation的概念。后续研究中,将其发展为cost volume。两个feature map的correlation的计算如下:
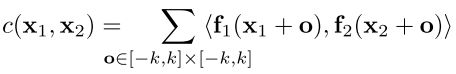
x 2 \bf{x}_2 x2取自于 x 1 \bf{x}_1 x1的一定矩形邻域内。取值时,文章中讲到:

可以看到,k取0,也就是每个算feature map1中每个像素的correlation时只与它自己有关。d则取得很大,是为了增大flow可以预测的范围。
FlowNet2.0(2017CVPR)
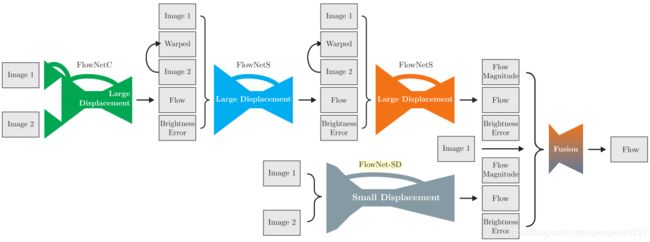
FlowNet2.0在网络架构上,将多个FlowNet串联起来,达到更好的效果。FlowNet-SD也可以看作为trick。除了在网络架构上做的创新,FlowNet2.0还探讨了如何训练的问题。
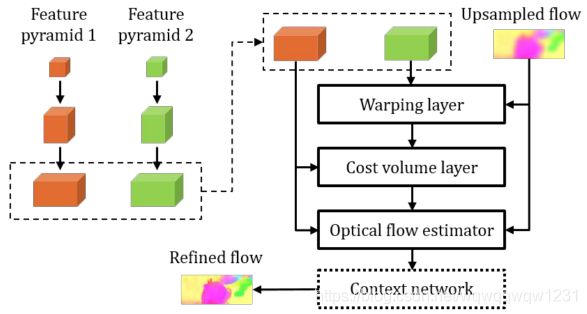
PWCNet(2018CVPR)
- 将从上一层获得flow进行upsample
- 通过flow,将feature map2的feature warp到feature map1,
- 计算cost volume,方式与FlowNet一样
- 然后通过cost volume得到这一层的volume
- 在顶层加入Context network
对比PWC-Net与FlowNet,可以发现,区别基本在于FlowNet只计算一次cost volume,而PWC-Net则计算很多次。warp的操作在FlowNet中也有。
MaskFlowNet(2020CVPR)
MaskFlowNet是目前比较新的改进,在KITTI上的效果也很好。主要是针对在前景移动了之后,背景中会有一些被遮挡的区域的问题。针对该问题,设计了在预测flow的同时,也预测被遮挡的的子任务。
相比于PWC-Net,先将feature map2 warp然后再计算cost volume,如下图:
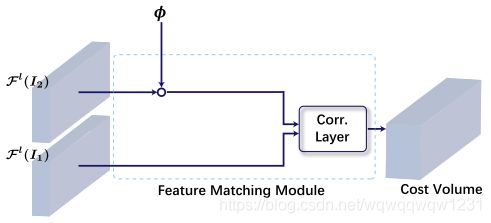
MaskFlowNet提出,对于warp后的feature map2(大小为[B, C, H, W]),先乘以预测的occlusion mask θ \theta θ (大小为[B, 1, H, W]),然后加上额外的特征 μ \mu μ(大小为[B, C, W, H])。得到如下结构:
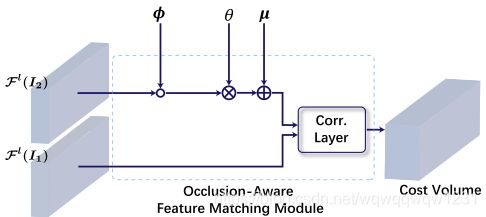
" μ \mu μ acts as a trade-off term that facilitates the learning of occlusions, as it provides extra information at the masked areas."
最后再加入Deformable Conv,将warp时使用插值变为Deform. Conv.,如下图

这就得到了AsymOFMM模块,然后多个模块的堆叠如下:

由此,借鉴FlowNet2.0中将网络堆叠的方法,提高flow的预测精度,得到MaskFlowNet:
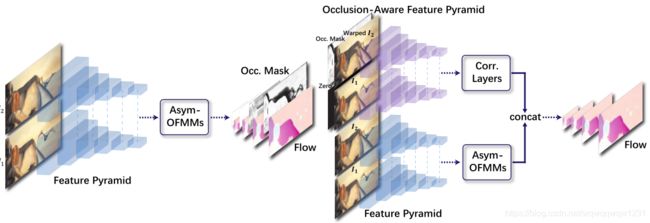
在ablation study中可以看到:
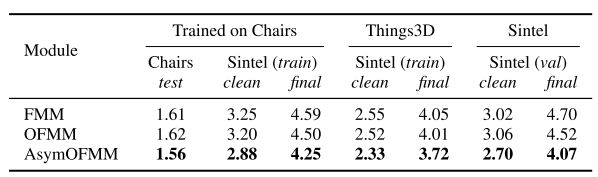
FMM对应PWC-Net中的模块,OFMM对应不加Deform. Conv.的模块。可以看到,其实Asym,也就是Deform. Conv.的提升非常大。
Sene Flow
Point-based
PointFlowNet(2019CVPR)
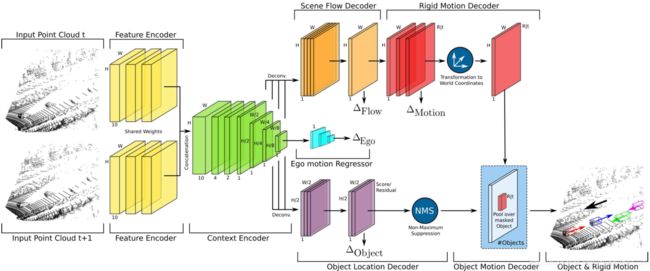
本方法也不是单纯的做Scene Flow,是把object detection结合起来。可以看到,做Scene Flow的部分其实就是FlowNetS
FlowNet3D(2019CVPR)
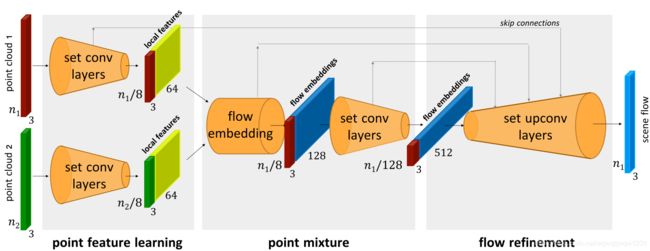
前面提取特征的主干网络是PointNet++,flow embedding部分如下:

其实就是把SA层变成了一个点云在另外一个点云中做group。相比于这相当于实现了FlowNetC中的correlation部分,就是feature map1中的每个点与feature map2中相关点求取correlation。但使用的MLP实现的。恢复原始点云的数量的过程upconv也是由SA实现的。
FlowNet3D++(2020WACV)
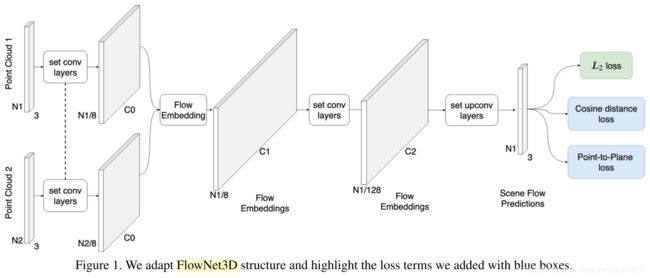
就是在FlowNet3D的基础上加了两个loss。一个配准常用的,一个是惩罚角度的。
HPLFlowNet(2019CVPR)
图也不知道该放啥。但具体架构其实和FlowNet3D差不多,只不过所有的主干换了。SA换成了DownBCL,upconv换成了UpBCL。correlation是用CorrBCL做的,但具体的公式如下:
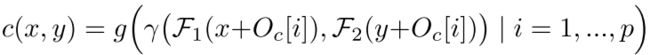
可以看到和FlowNet中的correlation也很像,文中说, γ \gamma γ使用concat做。这样子来说,其实实现更简单。
PointPWC-Net(2019arxiv)

从右图可以看到,这还就真是Point版的PWC-Net呗。那cost volume怎么算?
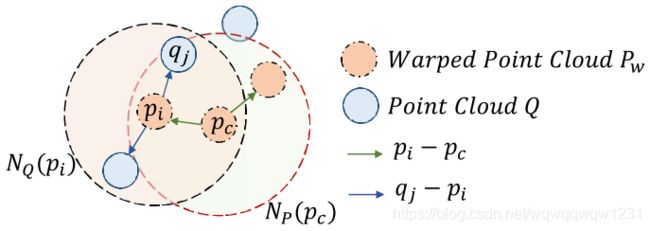
文中提出了一种patch to patch的方法。但其实也好理解。对于 P \bf{P} P中的一个点 p c p_c pc,那就在 P \bf{P} P中找到 p c p_c pc邻域内的所有点,对其中的每个点 p i p_i pi在 Q \bf{Q} Q中找邻域内所有点计算 p i p_i pi的cost,最后将所有的 p i p_i pi的cost相加得到 p c p_c pc的cost。有点RandLA那个味道A
Just Go with the Flow(2020CVPR)
Just Go with the Flow: Self-Supervised Scene Flow Estimation
本文并不是提出了新的网络,而是提出了自监督训练的方式。使用的网络是FlowNet3D。
自监督训练包含两个loss,一个是最近点的loss:
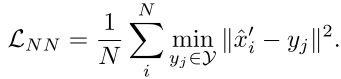
过程如下为:有两帧点云 X \bf{X} X和 Y \bf{Y} Y,有一个用于计算flow的网络g,1)通过 g ( X , Y ) g(\bf{X},\bf{Y}) g(X,Y)计算flow,并将第一帧warp到第二帧中,得到 X ^ ′ \hat{\bf{X}}' X^′。2)在Y中找 X ^ ′ \hat{\bf{X}}' X^′中每个点 x ^ ′ \hat{x}' x^′最近的点 y y y,然后计算两者位置差。
也就是其实使用最近点代替真值。
另一个是Anchored Cycle Consistency Loss:

过程如下:有两帧点云 X \bf{X} X和 Y \bf{Y} Y,有一个用于计算flow的网络g
1)通过 g ( X , Y ) g(\bf{X},\bf{Y}) g(X,Y)计算flow,并将第一帧warp到第二帧中,得到 X ^ ′ \hat{\bf{X}}' X^′。
2)在Y中找 X ^ ′ \hat{\bf{X}}' X^′中每个点 x ^ ′ \hat{x}' x^′最近的点 y y y,计算 x ‾ ′ = λ x ^ ′ + ( 1 − λ ) y \overline{x}'=\lambda\hat{x}'+(1-\lambda)y x′=λx^′+(1−λ)y得到 X ‾ ′ \overline{\bf{X}}' X′ 。
3)通过 g ( X ‾ ′ , X ) g(\overline{\bf{X}}',\bf{X}) g(X′,X),将 X ‾ ′ \overline{\bf{X}}' X′ 变换回第一帧得到 X ^ ′ ′ \hat{\bf{X}}'' X^′′。
Voxel-based
MotionNet (2020CVPR)

简单来说,俯视图中用FlowNetS。复杂点就是加了Spatio-temporal的东西在里面,但其实我觉得和Attention的思路就很像。