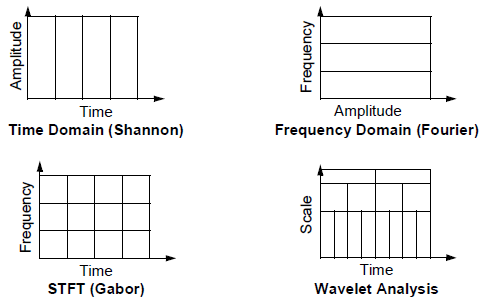
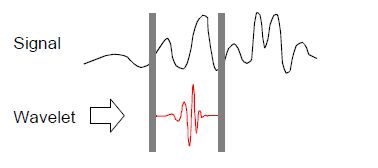
小波变换（wavelet transform）的通俗解释（二）
上篇文章已经说得很详细了，这边文章作为补充。
首先是一个宏观的例子：
相信大家都看过油画。 对于特别巨幅的油画， 不知道有没有过体会， 油画是只可远观而不可亵玩？ 当你在足够远的距离观察油画时， 油画所表达的内容是有层次且内容丰富的， 但是当你靠近油画甚至贴在油画上看时， 你只能看到一个个的小色块， 而此时这些小色块此时变成毫无意义的无规则排列。 我们假设油画中的每个小色块都对应某一信号中的某个瞬时时间，那么无数个小色块就拼凑成了整幅画， 相当于无数个瞬时时间片段组成了整个信号。那么，当我们想看看在这个信号的某个时间发生了什么的时候， 我们不得不试图靠近这幅画。
假设一个信号所包含的全部频率信息包含在一副无边无际的油画之中， 辣么， 当你和油画的距离为无穷远的时候你能够毫不费力的看清楚这幅画的全貌，（相当于傅立叶变换，可获得此信号的全部频率信息）， 但是你却无法看清楚这幅画的细节（无法得知此信号在某个时刻的瞬时频率）。 当你慢慢走向这幅画的时候（给傅立叶变换加窗）， 你走得越近（窗长越短）， 细节越清楚（信号的时间分辨率越来越高）， 也就是每个小色块都越来越清晰， 但每个色块所包含的信息量（频率信息）也越来越少，这就是著名的海森堡测不准原理（你永远无法得知一个信号之中任一时刻的准确频率信息， 即瞬时频率）， 也就是说你永远不可能在距离油画0 cm的位置观测出油画所画的内容。
如果，以上我的假设你都认同的话，辣么加窗傅立叶变换相当于你选择了一个固定的距离观察这幅油画，当距离近时（窗长减少）， 油画的细节更加清楚， 但是油画所表达的信息量随之减少。
这时候就有人提出来了，这个问题还不容易吗？ 油画在有的地方细节多，我们就离近一点看嘛（增大变换尺度，增加时间分辨率）；有的地方细节少，我们就离得稍微远一点看嘛（减小变化尺度，缩减时间分辨率），这样，在细节和内容的信息量上都能兼顾，能够更全面的欣赏这幅油画，这就是所谓的小波变换啦！其实这个原理非常简单， 题主可以想象我们看一副大型油画时，通常都是先离远点看看全貌， 然而对于一些细节丰富的地方，我们会走近观察。
最后总结： 傅立叶变换就相当于： 你只能在远距离观察油画； 加窗傅立叶变换相当于： 你只能在固定的距离观察油画； 而小波变换相当于，你可以在任意的距离观察油画。
作者：兔宝
链接：https://www.zhihu.com/question/22864189/answer/136518602
然后是另外一个解释，偏重于“为什么”，而不是“怎么做”。
——————————————————————————————————
信号分析已经有一些非常重要的工具了。 傅立叶分析是最著名的一个。 它将时间域的信号分解为不同频率的正旋信号。 另一种思路去分析傅立叶分析就是将时间域的信号分解为频率域的信号。
对于大多数信号而言， 傅立叶分析绝对是非常有用的，因为频率分析在大多数情况下都非常重要。 那么为什么我们还需要其他分析方法呢?
原因是因为傅立叶分析有一个非常严重的缺点。 在将信号从时间域变换到频率域去的时候，时间信息丢失了。 当我们在用傅立叶变化去分析一个具体信号的时候， 知道哪一个频率的信号在哪一个时间点出现的还是非常重要的。
如果一个信号并不随着时间变化太多， 那么我们称它为平稳信号。 那么知道哪一个频率的信号在哪一个时间点出现的就不那么重要了。 可是如果现实生活中我们研究的大多数信号都是非平稳信号，他们都许多非常短暂变化的特性： 漂移， 趋势， 突然变化， 开始和事件。 这些特点对于我们信号分析的特点， 傅立叶分析并不适合去做这种分析。
短时间傅立叶分析
为了克服这些缺点， Dennis Gabor (1946) 采用的傅立叶分析去分析一小部分时间域信号，这个技术叫做窗化一个信号，Gabor’s adaption， 称为短时间傅立叶转换， 将一个信号映射为关于时间和频率的一个二维函数。
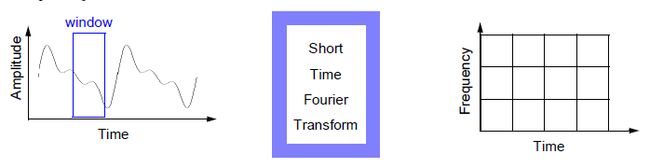
短时间傅立叶转换是一个时间和频率合作产生的信号。它主动提供了一些信息在时间和频率上一个信号产生。当然你可以获得这些信息通过一些有限的精度， 这些精度都是通过窗函数来决定的。
然后短时间傅立叶转换在短时间获得时间和频率的信息是有用的， 缺点是一旦你选择了特定尺寸的窗函数， 那么窗函数就对所有的频率都适用， 许多信号需要一个更灵活的方式， 我们可以选择窗的尺寸去决定时间或者频率
methodology
小波分析
小波分析代表下一个逻辑步骤： 一个窗函数在不同的区域内，小波分析准许用一个长的时间间隔当我们需要更精确的低频信息， 以及我们需要一个小的区域当我们需要更高频率的信息的时候
下面是一个基于时间对比， 频率对比， 以及短时间傅立叶分析的对比：
小波可以做什么呢？
一个最主要的优点是可以做局部的分析， 换句话说，就是可以分析一个局部的大信号。
比如说， 一个正旋信号有一个局部的不连续的点， 一个点是如此的小，以至于肉眼都看不到。 这样的信号在现实生活中可以很容易的产生了， 可能是能量传输断点，或者噪声开关。
一个傅立叶变换来分析这个信号，并没有什么特别的， 可以用小波分析来分析这个信号，就可以看出时间域的奇异点
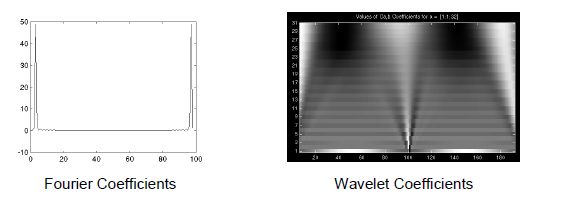
小波分析可以做一些其他分析方法不太能实现的功能， 比如变化趋势， 分解点， 更高维上的不连续点，自相似点。 更深远一点说，因为他提供了一个不同分析信号的视角
什么是小波分析 ？
现在我们已经知道了小波分析是很有用的， 那么什么是小波分析呢？ 以及什么是小波呢 ？
小波就是在有限距离上有均值为零值点的波形。
相比于正旋波， 这是傅立叶变化的基， 正旋波没有有限的距离， 他们从无穷小扩展到无穷大。 正旋波是光滑的和可以预测的， 小波是不规律的和非对称的。
傅立叶分析将一个信号分解为无数个不同频率的正旋信号的组合。 类似的， 小波分析将一个原始信号分解为移位过和压缩过的母小波的组合。
连续小波变化
从数学角度来说， 傅立叶分析可以被傅立叶变换表示出来：
这是将时间域的f(t) 和一个复杂的指数作一个倍乘（ 回想以下从欧拉法则， 一个复杂的指数形式可以分解为 实部和虚部 的正旋波形式： ）
傅立叶变换的结果就是得到傅立叶系数， 这是不同频率的正旋波在正交分解原始信号得到的对应分量。（如图）
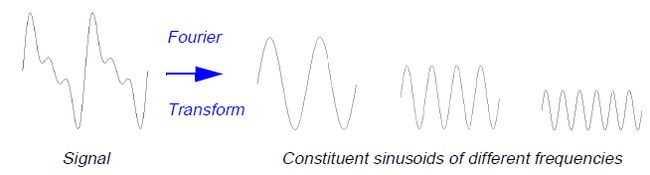
类似的， 小波分解，就是定义为原始时间域上的信号通过正交分解为不同转移过的，缩放过的小波组合。
这个变换的结果就是得到许多小波系数, C这些小波关于范围和位置的函数。
倍乘每个系数和对应的缩放过的和位移的小波，组成了这些原始的小波的组合
我们已经知道小波分析可以得到一系列关于时间－范围的小波信号的组合。
下面我们看一下什么是缩放。
缩放一个小波意味着伸展和压缩小波。
假设缩放参数为a, 拿正旋波来说：
那么这个缩放对于小波也是适用的。缩放因子越小， 小波越被压缩。
位移：
位移一个小波，意味着在小波峰值住作一个延时
五个简单的步骤的做连续小波变换：
连续小波变换
１． 取一个小波， 把它和信号的开始点做比较。
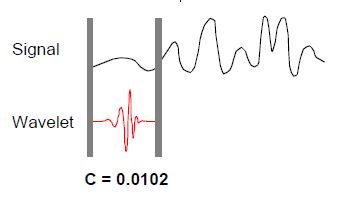
２． 计算一个数，c, 代表小波和这个区域内的信号有多接近， c越近，相似度越
高。这完全取决于你选择的小波形状
３． 位移小波， 重复１２ ，直到你完全运算完整个信号。
４． 缩小或者伸展真整个小波， 重复１，２，３
5． 重复整个操作直到１，２，３，４ 全部做完
转载自知乎：https://www.zhihu.com/question/22864189
用户“bellaxia”的回答。