Delaunay三角剖分及matlab实例
鉴于Delaunay三角剖分在点云拟合方面有不错的应用,现对该算法的原理进行简单的汇总~
----------------------------原理部分------------------------
点集的三角剖分(Triangulation),对数值分析(如有限元分析)以及图形学来说,都是极为重要的预处理技术。尤其是Delaunay三角剖分,关于点集的很多种几何图都和Delaunay三角剖分相关,如Voronoi图,EMST树等。Delaunay三角剖分有最大化最小角“最接近于规则化的“的三角网和唯一性(任意四点不能共圆)两个特点。Delaunay三角剖分是变现三维形状的基础。可以通过这个物体的投影来建立二维视觉图,并用二维Delaunay三角剖分来分析识别该物体,或者将它与实物相比较。Delaunay剖分是连接计算机视觉与计算机图形学的桥梁。以下内容参考:http://www.cnblogs.com/RenLiQQ/archive/2008/02/06/1065399.html
1、三角剖分与Delaunay剖分的定义
如何把一个离散几何剖分成不均匀的三角形网格,这就是离散点的三角剖分问题,散点集的三角剖分,对数值分析以及图形学来说,都是极为重要的一项处理技术。该问题图示如下:![]()
1.1 三角剖分定义
【定义】三角剖分:假设V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段,E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件:1、除了端点,平面图中的边不包含点集中的任何点。
2、没有相交边。//边和边没有交叉点
3、平面图中所有的面都是三角面,且所有三角面的合集是散点集V的凸包。
//凸包的概念:用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有的点。
1.2 Delaunay三角剖分的定义
在实际中运用的最多的三角剖分是Delaunay三角剖分,它是一种特殊的三角剖分。先从Delaunay边说起:【定义】Delaunay边:假设E中的一条边e(两个端点为a,b),e若满足下列条件,则称之为Delaunay边:存在一个圆经过a,b亮点,圆内(注意是园内,圆上最多三点共圆)不含点集V中任何其他的点,这一特性又称空圆特性。
【定义】Delaunay三角剖分:如果点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。
1.3 Delaunay三角剖分的准则
要满足Delaunay三角剖分的定义,必须符合两个重要的准则:1、空圆特性:Delaunay三角网是唯一的(任意四点不能共圆),在Delaunay三角形网中任一三角形的外接圆范围内不会有其它点存在。如下图所示:
![]()
2、最大化最小角特性:在散点集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大。从这个意义上讲,Delaunay三角网是“最接近于规则化的”三角网。具体的说是在两个相邻的三角形构成凸四边形的对角线,在相互交换后,两个内角的最小角不再增大。如下图所示:![]()
1.4 Delaunay三角剖分的特性
以下是Delaunay剖分所具备的优异特性:1、最接近:以最接近的 三点形成三角形,且各线段(三角行的边)皆不相交。
2、唯一性:不论从区域何处开始构建,最终都将得到一致的结果。
3、最优性:任意两个相邻三角形构成的凸四边形的对角线如果可以互换,那么两个三角形六个内角中最小角度不会变化。
4、最规则:如果将三角网中的每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大。
5、区域性:新增、删除、移动某一个顶点只会影响邻近的三角形。
6、具有凸边形的外壳:三角网最外层的边界形成一个凸多边形的外壳。
1.5局部最优化处理
理论上为了构造Delaunay三角网,Lawson提出的局部优化过程LOP(Local Optimization Procedure),一般三角网经过LOP处理,即可确保为Delaunay三角网,其基本做法如下所示:1、将两个具有共同边的三角形合成一个多边形。
2、以最大空圆准则作检查,看其第四个顶点是否在三角形的外接圆内。
3、如果在,修正对角线即将对角线对调,即完成局部优化过程的处理。
LOP处理过程如下图所示:
![]()
1.6三维空间情形
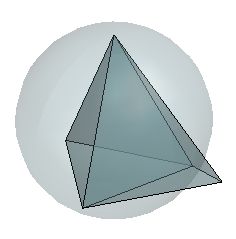
Delaunay三角网格的性质可以推广到高维。一个三维点集的三角剖分是由四面体构成。下图显示了一个由两个四面体构成的简单三维Delaunay三角剖分。一个四面体的外接球来说明空接球准则。
2.Delaunay剖分的算法
Delaunay剖分是一种三角剖分的标准,实现它有多种算法。2.1.Lawson算法
逐点插入的Lawson算法是Lawson在1977年提出的,该算法思路简单,易于编程实现。基本原理为:首先建立一个大的三角形或多边形,把所有数据点包围起来,向其中插入一点,该点与包含它的三角形三个顶点相连,形成三个新的三角形,然后逐个对它们进行空外接圆检测,同时用Lawson设计的局部优化过程LOP进行优化,即通过交换对角线的方法来保证所形成的三角网为Delaunay三角网。上述基于散点的构网算法理论严密、唯一性好,网格满足空圆特性,较为理想。由其逐点插入的构网过程可知,遇到非Delaunay边时,通过删除调整,可以构造形成新的Delaunay边。在完成构网后,增加新点时,无需对所有的点进行重新构网,只需对新点的影响三角形范围进行局部联网,且局部联网的方法简单易行。同样,点的删除、移动也可快速动态地进行。但在实际应用当中,这种构网算法当点集较大时构网速度也较慢,如果点集范围是非凸区域或者存在内环,则会产生非法三角形。
2.2.Bowyer-Watson算法 (推荐)
目前采用逐点插入方式生成的Delaunay三角网的算法主要基于Bowyer-Watson算法,Bowyer-Watson算法的主要步骤如下:1、构造一个超级三角形,包含所有散点,放入三角形链表。
2、将点集中的散点依次插入,在三角形链表中找出其外接圆包含插入点的三角形(称为该点的影响三角形),删除影响三角形的公共边,将插入点同影响三角形的全部顶点连接起来,从而完成一个点在Delaunay三角形链表中的插入。
3、根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入Delaunay三角形链表。
4、循环执行上述第2步,直到所有散点插入完毕。
这一算法的关键的第2步图示如下:
![]()
2.3伪代码表述
input: 顶点列表(vertices) //vertices为外部生成的随机或乱序顶点列表
output:已确定的三角形列表(triangles)
初始化顶点列表
创建索引列表(indices = new Array(vertices.length)) //indices数组中的值为0,1,2,3,......,vertices.length-1
基于vertices中的顶点x坐标对indices进行sort //sort后的indices值顺序为顶点坐标x从小到大排序(也可对y坐标,本例中针对x坐标)
确定超级三角形
将超级三角形保存至未确定三角形列表(temp triangles)
将超级三角形push到triangles列表
遍历基于indices顺序的vertices中每一个点 //基于indices后,则顶点则是由x从小到大出现
初始化边缓存数组(edge buffer)
遍历temp triangles中的每一个三角形
计算该三角形的圆心和半径
如果该点在外接圆的右侧
则该三角形为Delaunay三角形,保存到triangles
并在temp里去除掉
跳过
如果该点在外接圆外(即也不是外接圆右侧)
则该三角形为不确定 //后面会在问题中讨论
跳过
如果该点在外接圆内
则该三角形不为Delaunay三角形
将三边保存至edge buffer
在temp中去除掉该三角形
对edge buffer进行去重
将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中
将triangles与temp triangles进行合并
除去与超级三角形有关的三角形
end以下摘自:http://www.cnblogs.com/zhiyishou/p/4430017.html
用图来解释伪代码过程,先用三点来做实例:
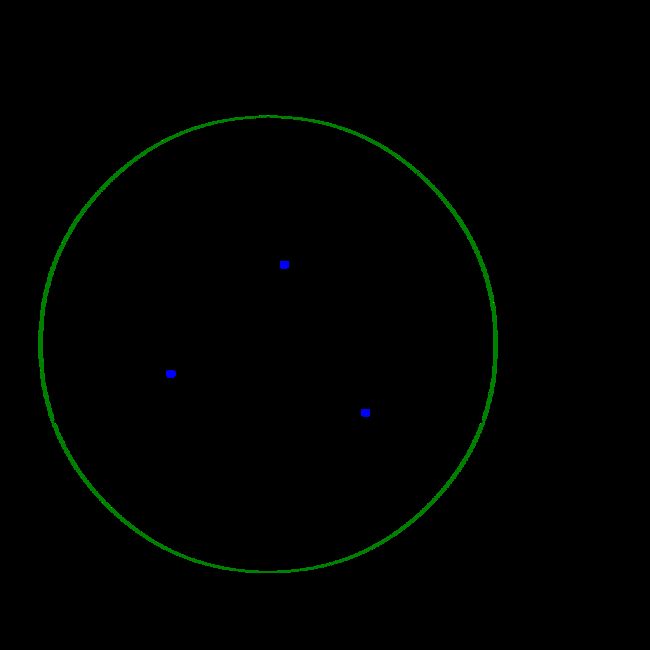
如图,随机的三个点
根据离散点的最大分布来求得随机一个超级三角形(超级三角形意味着该三角形包含了点集中所有的点),方法是根据相似三角形定理求得与矩形一半的小矩形的对角三角形,扩大一倍后则扩大后的直角三角形斜边经过点(Xmax,Ymin),但是为了将所有的点包含在超级三角形内,在右下角对该三角形的顶点进行了横和高的扩展,并要保证这个扩展三角形底大于高,才能实现包含。这样求得的超级三角形不会特别大使得计算复杂,而且过程也简单,并将超级三角形放入temp triangles中。
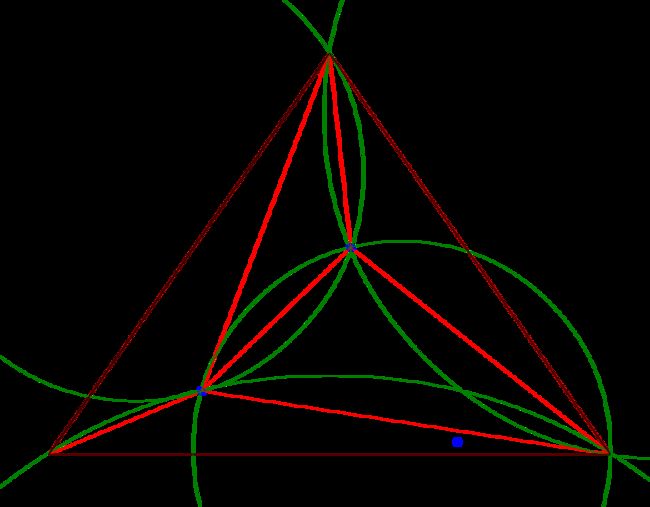
接下来就像是伪代码中描述的那样,对temp triangle中的的三角形遍历画外接圆,这时先对左边的第一个点进行判断,其在圆内,所以该三角形不为Delaunay三角形,将其三边保存至edge buffer中,temp triangle中删除该三角形。
将该点与edge buffer中的每一个边相连,组成三个三角形,加入到temp triangles中,
再将重复对temp triangles的遍历并画外接圆,这时使用的是第二个点来进行判断
- 该点在三角形1外接圆右侧,则表示左侧三角形为Delaunay三角形,将该三角形保存至triangles中
- 该点在三角形2外接圆外侧,为不确定三角形,所以跳过(后面会讲到为什么要跳过该三角形),但并不在temp triangles中删除
- 该点在三角形3外接圆内侧,则这时向清空后的edge buffer加入该三角形的三条边,并用该点写edge buffer中的三角边进行组合,组合成了三个三角形并加入到temp triangles中
再次对temp triangles进行遍历,这里该数组里则含有四个三角形,一个是上次检查跳过的含有第一个点的三角形和新根据第二个点生成的三个三角形
- 该点在三角形1外接圆右侧,则该三角形为Delaunay三角形,保存至triangles中,并在temp triangles中删除
- 该点在三角形2外接圆外侧,跳过
- 该点在三角形3外接圆内侧,将该三边保存至temp buffer中,并在temp triangles中删除
- 该点在三角形4外接圆内侧,将该三边保存至temp buffer中,并在temp triangles中删除
这时,temp buffer 中有六条边,triangles中有两个三角形,temp triangles中有1个三角形,对temp buffer中的六条边进行去重,得到五条边,将该点与这五条边组合成五个三角形并加入到temp triagnles 中,这时temp triangles中有6个三角形
由于三个点已经遍历结束,到了不会再对第三个点形成的三角形做外接圆,这时则将triangles与temp trianlges合并,合并后的数组表示包含已经确定的Delaunay三角形和剩下的三角形。这时除去合并后数组中的和超级三角形三个点有关的所有三角形,即进行数组坐标的限定,则得到了最后的结果:
----------------------------代码部分------------------------
实例1:(Matlab)
clear all;clc;close all;
%load seamount
[x,y,z]=peaks;
plot3(x,y,z);
%plot(x,y,'.','markersize',10)
xlabel('x'), ylabel('y')
grid on
tri = delaunay(x,y);
hold on, triplot(tri,x,y), hold off
figure
hidden on
trimesh(tri,x,y,z)
xlabel('x'),ylabel('y'),zlabel('Depth z');
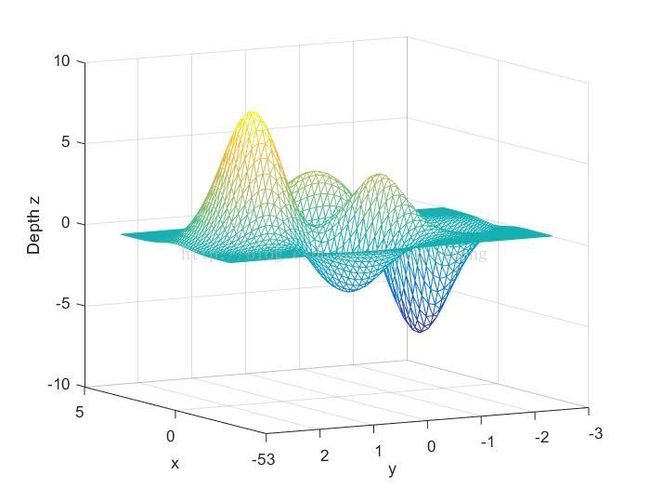
左图为peaks函数的三维图形,有图为使用dalaunay三角剖分得到的三维模型,对比。
另外,在http://blog.csdn.net/newthinker_wei/article/details/45598769这篇博文里有使用opencv进行dalaunay三角剖分的讲述。
参考:
https://en.wikipedia.org/wiki/Delaunay_triangulation
http://www.cnblogs.com/RenLiQQ/archive/2008/02/06/1065399.html
http://www.linuxidc.com/Linux/2014-04/100131.htm
http://blog.csdn.net/newthinker_wei/article/details/45598769
http://cn.mathworks.com/help/matlab/math/delaunay-triangulation.html