python 实现单因素方差分析（1）

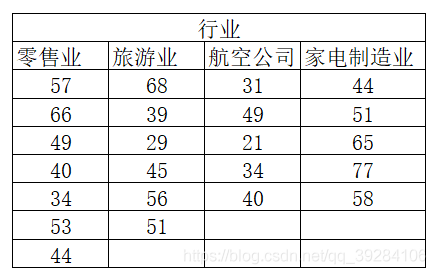
案例：

分析行业对被投诉次数是否有显著影响（）

提出假设：

由于变量行业有4个水平，分别是零售业、旅游业、航空公司和家电制造业，那么为了检验这4个水平（每个水平代表一个总体）的均值是否相等，需要提出如下的假设：

       行业对被投诉次数没有显著影响

 不完全相等  行业对被投诉次数有显著影响

# 导入相关包
import pandas as pd
import numpy as np
import math
import scipy
from scipy import stats 

# 自定义函数

def SST(Y):
    sst = sum(np.power(Y - np.mean(Y), 2))
    return sst

def SSA(data, x_name, y_name):
    total_avg = np.mean(data[y_name])
    df = data.groupby([x_name]).agg(['mean', 'count'])
    df = df[y_name]
    ssa = sum(df["count"]*(np.power(df["mean"] - total_avg, 2)))
    return ssa

def SSE(data, x_name, y_name):
    df = data.groupby([x_name]).agg(['mean'])
    df = df[y_name]
    dict_ = dict(df["mean"])
    data_ = data[[x_name, y_name]]
    data_["add_mean"] = data_[x_name].map(lambda x: dict_[x])
    sse = sum(np.power(data_[y_name] - data_["add_mean"], 2))
    return sse

def one_way_anova(data, x_name, y_name, alpha=0.05):
    n = len(data)                     # 总观测值数
    k = len(data[x_name].unique())    # 变量水平个数
    
    sst = SST(data[y_name])           # 总平方和
    ssa = SSA(data, x_name, y_name)   # 组间平方和
    sse = SSE(data, x_name, y_name)   # 组内平方和
    
    msa = ssa / (k-1)  # 组间均方 或 组间方差
    mse = sse / (n-k)  # 组内均方 或 组内方差
    F = msa / mse      # 检验统计量F
    pf = scipy.stats.f.sf(F, k-1, n-k)  
    Fa = scipy.stats.f.isf(alpha, dfn=k-1, dfd=n-k)   # F临界值
    
    r_square = ssa / sst  # 自变量与因变量的关系强度表示
    
    table = pd.DataFrame({'差异源':['组间', '组内', '总和'],
                          '平方和SS':[ssa, sse, sst],
                          '自由度df':[k-1, n-k, n-1],
                          '均方MS':[msa, mse, '_'],
                          'F值':[F, '_', '_'],
                          'P值':[pf, '_', '_'],
                          'F临界值':[Fa, '_', '_'],
                          'R^2':[r_square, '_', '_']})
    
    return table

# 导入数据
df = pd.read_excel("E:\\xx业务数据.xlsx", sheet_name='source_02')
df.rename(columns={'行业':'X', '被投诉次数':'Y'}, inplace=True)

# 输出方差分析结果
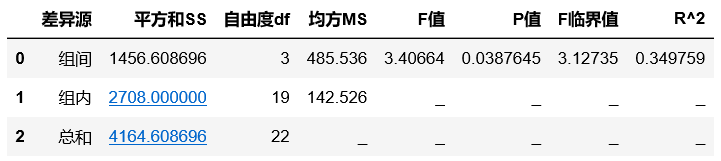
one_way_anova(df, 'X', 'Y', alpha=0.05)

根据以上单因素方差分析结果解释如下：

（1）行业：P-value=0.0387645 <  (或 F值=3.40664>F临界值=3.12735），拒绝原假设。表明行业对被投诉次数有显著影响。