JAVA程序设计：设计跳表（LeetCode：1206）

不使用任何库函数，设计一个跳表。

跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90]，然后增加 80、45 到跳表中，以下图的方式操作：

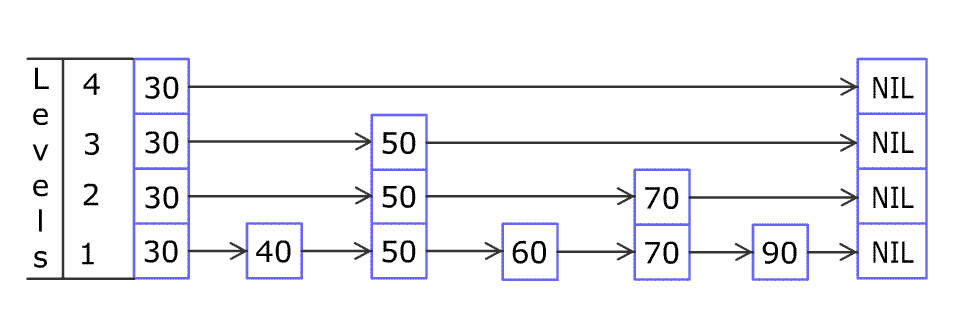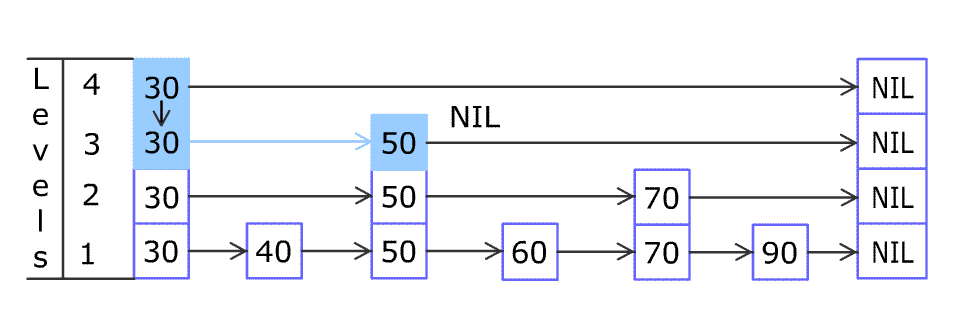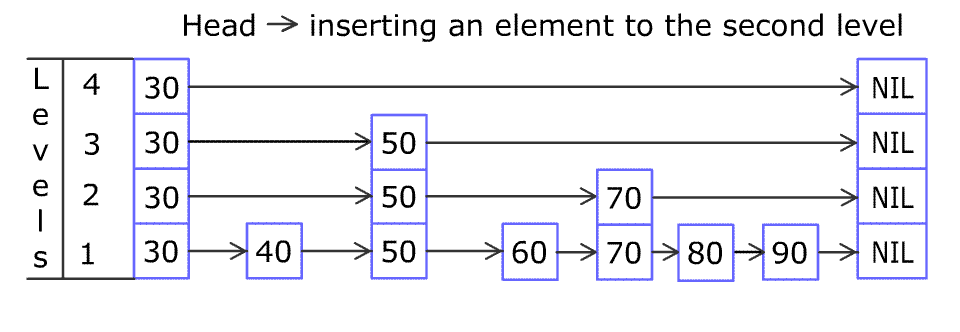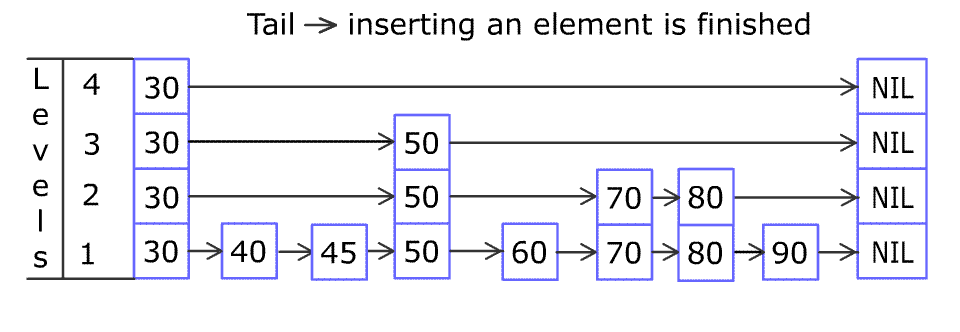
Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

在本题中，你的设计应该要包含这些函数：

bool search(int target) : 返回target是否存在于跳表中。
void add(int num): 插入一个元素到跳表。
bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。
了解更多 : https://en.wikipedia.org/wiki/Skip_list

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

样例:

Skiplist skiplist = new Skiplist();

skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除
约束条件:

0 <= num, target <= 20000
最多调用 50000 次 search, add, 以及 erase操作。

方法一：用数组+set实现快速插入，删除以及查询操作，并且能够做到比跳表更优，不过违背了本题的初衷。

class Skiplist {

    int[] nums;
    Set st;

    public Skiplist() {
        nums = new int[20005];
        st = new HashSet<>();
    }

    public boolean search(int target) {
        return st.contains(target);
    }

    public void add(int num) {
        st.add(num);
        nums[num]++;
    }

    public boolean erase(int num) {
        if (nums[num] == 0)
            return false;
        nums[num]--;
        if (nums[num] == 0)
            st.remove(num);
        return true;
    }
}

方法二：我们采用链表实现，每个节点分别存储节点的值、该链上下一个节点以及下一层链表的对应节点。

class Skiplist {

    class node {
        int val;
        node next, down;

        public node(int val, node next, node down) {
            this.val = val;
            this.next = next;
            this.down = down;
        }
    }

    private node head;

    public Skiplist() {
        head = new node(-1, null, null);
    }

    public boolean search(int target) {
        node now = head;
        while (now != null) {
            while (now.next != null && now.next.val < target)
                now = now.next;
            if (now.next == null || now.next.val > target)
                now = now.down;
            else
                return true;
        }
        return false;
    }

    public void add(int num) {
        List list = new ArrayList<>();
        node now = head;
        while (now != null) {
            while (now.next != null && now.next.val < num)
                now = now.next;
            list.add(now);
            now = now.down;
        }

        node downNode = null;
        boolean insertUp = true;
        int index = list.size() - 1;

        while (insertUp && index >= 0) {
            node curInsert = list.get(index);
            list.remove(index--);
            curInsert.next = new node(num, curInsert.next, downNode);
            downNode = curInsert.next;
            int randint = (int) (1 + Math.random() * (10 - 1 + 1));
            //产生1-10的随机数（只要是偶数长度范围内的随机数即可）
            insertUp = (randint % 2 == 0 ? true : false);//50%的概率在上层插值
        }
        if (insertUp)
            head = new node(-1, new node(num, null, downNode), head);
    }

    public boolean erase(int num) {
        node now = head;
        boolean seen = false;
        while (now != null) {
            while (now.next != null && now.next.val < num)
                now = now.next;
            if (now.next == null || now.next.val > num)
                now = now.down;
            else {
                seen = true;
                now.next = now.next.next;
                now = now.down;
            }
        }
        return seen;
    }
}