FPGA图像处理基础----cordic算法原理以及实现(1)
Cordic算法的基本原理
在FPGA中实现开根号正余弦这种操作是比较难实现的。FPGA的特性决定了其较难处理浮点类型的数据。但是通过Cordic算法可以使得FPGA能够来处理这种开根号和正余弦的计算。
使用坐标的旋转能够比较直观地表现出这一算法的实现原理。我也是在参考了两位前辈的博客,再结合《基于FPGA的数字图像处理》这本书上的知识,来理解和学习这一算法。
这两位的博客写的通俗易懂。
1.基于FPGA的Cordic算法实现
2.CORDIC算法的FPGA实现
1. 旋转模式下的Cordic过程
在下图中有两个点P1(X1,Y1),P0(X0,Y0),两着到圆心的距离相同,若P0想要通过选择得到P1。假设P0和P1之间的夹角为θ,P1与x轴正半轴夹角为ɑ,为方便计算,假定P0,P1到原点的距离为1;可以有如下表达式:
x0 = cos( θ + ɑ) = cosθcosɑ - sinθsinɑ
y0 = sin( θ + ɑ) = cosθsinɑ + sinθcosɑ
x1 = cosɑ
y1 = sinɑ
可以得到:
x0 = cosθ * x1 - sinθ * y1
y0 = cosθ * y1 + sinθ * x1
上面的关系式就是下图中所示的矩阵表达坐标旋转的公式。矩阵的知识,早已忘记,但是这个旋转还是能够很明显看出来的。
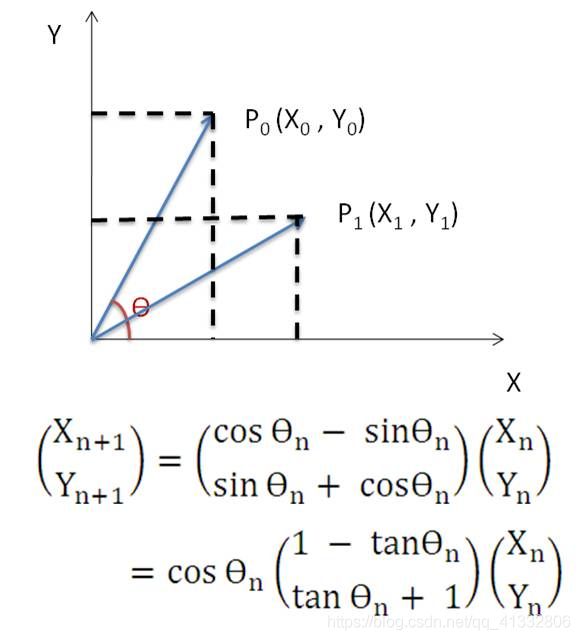
上面的式子,表示的是,经过n此旋转后,(X0,Y0)最终旋转到了(X1,Y1)。接下来就是Cordic算法最有意思的地方了,让上面的tanθn在每次旋转的时候都对应一个固定的值tanθn = 2^(-n);
这样在每次旋转过程中,对应那一次的旋转的角度都是一个固定的值。其值的大小等于arctan(2^(-n));
链接1的博客中,可以看到每次移动角度如下:
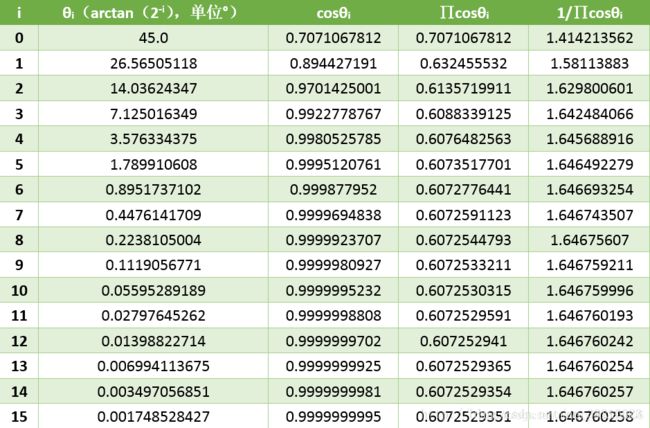
从θn的迭代公式中可以看到,其有一个符号位Sn,这个Sn用来表示要旋转的方向。举个简单的例子,若P0处于X轴正半轴上,要沿着单位圆移动到与x轴正半轴夹角位30°的地方,那么它的迭代过程是这样的。
n=0: 第一次旋转Sn = 1,逆时针旋转arctan(2^(0));旋转到的角度大于30°
n=1: 第二次旋转Sn = -1, 顺时针旋转arctan(2^(-1)); 旋转到的角度小于30°
n=2: 第三次旋转Sn = 1, 逆时针旋转arctan(2^(-2));旋转到的角度大于30°
。。。
经过多次迭代过后,可以从上面的表格中看到,多次迭代后的旋转迭代角度已经非常接近0了,说明多次迭代后,离目标点十分接近,在误差允许范围内,就可以认为当前已经旋转到了目标点的位置。
下图中的θn就是就是每次迭代过程中需要旋转的角度。
Sn代表每次迭代旋转过程中的旋转方向。
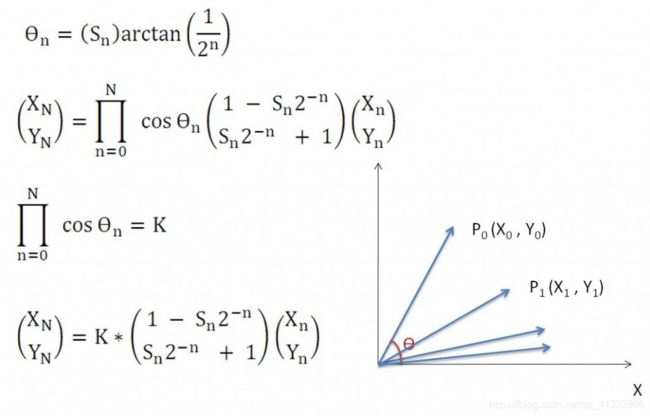
因为每次旋转的角度是确定的,因此对于确定迭代次数的旋转过程,其前面cosθn的累积也是一个固定的常数,这个累计可以用K表示,称作模长校正因子。由此,可以得到如下的迭代关系式。从而将复杂的运算,转换成了FPGA便于实现的移位和加法运算。
Xn+1 = Xn - Sn* Yn* 2^(-n)
Yn+1 = Yn + Sn* Xn* 2^(-n)
Zn+1 = Zn – Sn * arctan(2^(-n))
2. 基于Cordic求任意坐标的模长和角度
在前面介绍了Cordic实现的基本原理,在图像处理,比如进行Sobel算子处理时,需要求取两个方向上梯度的平方根和梯度的方向。此时才作用Cordic就能够比较简单的实现求平方根和角度的运算。
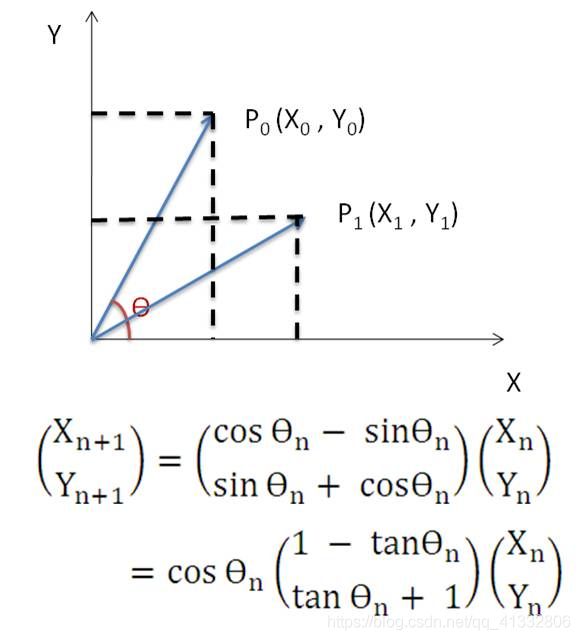
假设输入的坐标位P0经过迭代旋转后,旋转到了X轴正半轴,那么此时,得到的P1的横坐标就是求得的平方根的值,得到的角度,取绝对值就是该点在极坐标的下角度。从上面的表格图中可以看到,使用Cordic算法时,能旋转的最大的角度大致处于[-97°,97°]之间。因此在处理任意角度时,可以将其移动到第一象限,求得模长和角度后,再还原到原来的象限中即可。在旋转过程中,可以根据Yn的大小来确定旋转的方向,若Yn>=0则Sn = 1,若Yn < 0则Sn = -1;
3. Cordic求模和角度Veriog实现
3.1 预处理模块
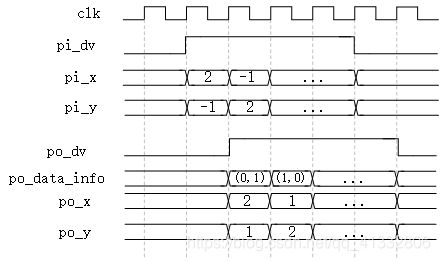
预处理模块完成的是,将给定的输入的坐标,映射到第一象限中,并使用寄存器保存输入坐标的象限信息,便于在Cordic运算完成之后,恢复象限信息。
`timescale 1ns / 1ps
module cordic_pre(
input wire clk ,
input wire rst ,
input wire pi_dv ,
input wire [15:0] pi_x ,//输入横坐标
input wire [15:0] pi_y ,//输入纵坐标
output wire po_dv ,
output wire [15:0] po_x ,//输出横坐标
output wire [15:0] po_y ,//输出纵坐标
output wire [1:0] data_info //保存坐标的象限信息
);
reg [15:0] abs_x ;//x,y绝对值
reg [15:0] abs_y ;
reg [1:0] quadrant_r ;
reg po_dv_r ;
assign po_x = abs_x;
assign po_y = abs_y;
assign data_info = quadrant_r;
assign po_dv = po_dv_r;
//==========================================
//保存象限信息,并且将坐标转移到第一象限
//1 clk
//==========================================
always @(posedge clk) begin
if (rst==1'b1) begin
quadrant_r <= 'd0;
abs_x <= 'd0;
abs_y <= 'd0;
end
else if(pi_dv == 1'b1)begin
case({pi_x[15], pi_y[15]})
//第一象限
2'b00 : begin
quadrant_r <= 2'b00;
abs_x <= pi_x;
abs_y <= pi_y;
end
//第四象限
2'b01 : begin
quadrant_r <= 2'b01;
abs_x <= pi_x;
abs_y <= ~pi_y + 1'b1;
end
//第二象限
2'b10 : begin
quadrant_r <= 2'b10;
abs_x <= ~pi_x + 1'b1;
abs_y <= pi_y;
end
//第三象限
2'b11 : begin
quadrant_r <= 2'b11;
abs_x <= ~pi_x + 1'b1;
abs_y <= ~pi_y + 1'b1;
end
endcase
end
else begin
quadrant_r <= 2'b00;
abs_x <= 'd0;
abs_y <= 'd0;
end
end
always @(posedge clk) begin
if (rst == 1'b1) begin
po_dv_r <= 2'b00;
end
else begin
po_dv_r <= pi_dv;
end
end
endmodule
3.2 迭代处理单元
3.2.1 单个迭代处理单元
在迭代处理的过程中,可以将角度进行量化,也即将2π映射到一个区间当中,映射区间越大,响应的精度也就越高,占用的资源也就越多。在本人实现过程中,参照《基于FPGA的数字图像处理》这本书,将2π映射到2^(20)这个区间当中。
因为每次迭代需要旋转的角度是固定的,因此可以使用ram提前将映射完成后的数据存储起来。
`timescale 1ns / 1ps
module cordic_unit(
input wire clk ,
input wire rst ,
input wire pi_dv ,
input wire [19:0] pi_z ,//输入初始角度
input wire [19:0] pi_x ,//输入横坐标(归一化后的位宽)
input wire [19:0] pi_y ,//输入纵坐标(归一化后的位宽)
input wire [1:0] pi_data_info ,//保存坐标的象限信息
output wire po_dv ,
output wire [19:0] po_z ,//输出角度
output wire [19:0] po_x ,//输出横坐标(归一化后的位宽)
output wire [19:0] po_y ,//输出纵坐标(归一化后的位宽)
output wire [1:0] po_data_info //保存坐标的象限信息
);
//==========================================
//parameter define
//==========================================
parameter ITERATION_IDX = 0 ;//迭代次数
//==========================================
//internal signals
//==========================================
reg signed [19:0] delta_z ;//角度变化量
reg signed [19:0] delta_x ;//x坐标变化量
reg signed [19:0] delta_y ;//y坐标变化量
reg symbol ;//旋转方向
reg [19:0] pi_x_dd ;//延时一拍以便和变化量相加
reg [19:0] pi_y_dd ;
reg [19:0] pi_z_dd ;
reg [19:0] po_x_r ;//延时一拍以便和变化量相加
reg [19:0] po_y_r ;
reg [19:0] po_z_r ;
reg [1:0] po_dv_r ;
reg [3:0] po_data_info_r ;
assign po_x = po_x_r;
assign po_y = po_y_r;
assign po_z = po_z_r;
assign po_dv = po_dv_r[1];
assign po_data_info = po_data_info_r[3:2];
//==========================================
// 迭代角度查找表,一共迭代16次认位此时已经满足
// 最小误差要求,角度是经过归一化的,归一化方式:2π = 2^20;
// 将2π映射到[0,2^20 -1]
// arctan(1/(2^0)) = 0x20000
// arctan(1/(2^1)) = 0x12E40
// ......
// arctan(1/(2^15)) = 0x05
// arctan(1/(2^16)) = 0x03
// arctan(1/(2^17)) = 0x01
//==========================================
wire [19: 0] arctan_lut[0: 17];
assign arctan_lut[0] = 20'h20000;
assign arctan_lut[1] = 20'h12E40;
assign arctan_lut[2] = 20'h09FB4;
assign arctan_lut[3] = 20'h05111;
assign arctan_lut[4] = 20'h028B1;
assign arctan_lut[5] = 20'h0145D;
assign arctan_lut[6] = 20'h00A2F;
assign arctan_lut[7] = 20'h00518;
assign arctan_lut[8] = 20'h0028C;
assign arctan_lut[9] = 20'h00146;
assign arctan_lut[10] = 20'h000A3;
assign arctan_lut[11] = 20'h00051;
assign arctan_lut[12] = 20'h00029;
assign arctan_lut[13] = 20'h00014;
assign arctan_lut[14] = 20'h0000A;
assign arctan_lut[15] = 20'h00005;
assign arctan_lut[16] = 20'h00003;
assign arctan_lut[17] = 20'h00001;
//==========================================
//迭代公式:Sn为旋转的方向,需要根据当前纵坐标来判断:
// Yn >= 0当前还未旋转到 X轴, 需要顺时针旋转 Sn = 1;
// Yn < 0 当前旋转到第四象限, 需要逆时针旋转 Sn = -1;
// (Yn >= 0) ? (Sn = -1) : (Sn = 1)
// X(n + 1) = Xn - Sn * 2^(-n) * Yn
// Y(n + 1) = Yn + Sn * 2^(-n) * Xn
// Z(n + 1) = Xn - Sn * arctan(2^(-n))
//
//delta_x = 2^(-n) * Yn
//delta_y = 2^(-n) * Xn
//symbol = (Yn > 0) ? 1 : 0;
//==========================================
//--------------第0次迭代--------------------
//delta_x 是X方向上变化的值,
//delta_y 是y方向上变化的值,
//迭代以流水线方式进行,以面积换取速度
generate
if (ITERATION_IDX == 'd0) begin : non_shift
always @(posedge clk) begin
if (rst==1'b1) begin
delta_x <= 'd0;
delta_y <= 'd0;
symbol <= 1'b0;
end
else if(pi_dv == 1'b1)begin
delta_x <= pi_y;
delta_y <= pi_x;
symbol <= 1'b1;
end
else begin
delta_x <= 'd0;
delta_y <= 'd0;
symbol <= 1'b0;
end
end
end
endgenerate
//----------------第1~15次迭代------------------
generate
if (ITERATION_IDX != 'd0) begin
always @(posedge clk) begin
if (rst==1'b1) begin
delta_x <= 'd0;
delta_y <= 'd0;
symbol <= 1'b0;
end
//根据当前坐标,确定变化量的值,并且给出旋转方向
//带符号的移位操作
else begin
case({pi_x[19], pi_y[19]})
2'b00 : begin
delta_x <= {{ITERATION_IDX{1'b0}}, pi_y[19 : ITERATION_IDX]};
delta_y <= {{ITERATION_IDX{1'b0}}, pi_x[19 : ITERATION_IDX]};
symbol <= 1'b1;
end
2'b01 : begin
delta_x <= {{ITERATION_IDX{1'b1}}, pi_y[19 : ITERATION_IDX]};
delta_y <= {{ITERATION_IDX{1'b0}}, pi_x[19 : ITERATION_IDX]};
symbol <= 1'b0;
end
2'b10 : begin
delta_x <= {{ITERATION_IDX{1'b0}}, pi_y[19 : ITERATION_IDX]};
delta_y <= {{ITERATION_IDX{1'b1}}, pi_x[19 : ITERATION_IDX]};
symbol <= 1'b1;
end
2'b11 : begin
delta_x <= {{ITERATION_IDX{1'b1}}, pi_y[19 : ITERATION_IDX]};
delta_y <= {{ITERATION_IDX{1'b1}}, pi_x[19 : ITERATION_IDX]};
symbol <= 1'b0;
end
endcase
end
end
end
endgenerate
//==========================================
//每次迭代角度变化量,每次迭代的角度大小是固定的,
//迭代时需要注意角度变化的方向(顺时针,逆时针)
//旋转方向需要根据当前点的纵坐标的符号来判断
//==========================================
always @(posedge clk) begin
if (rst==1'b1) begin
delta_z <= 'd0;
end
else begin
delta_z <= arctan_lut[ITERATION_IDX];
end
end
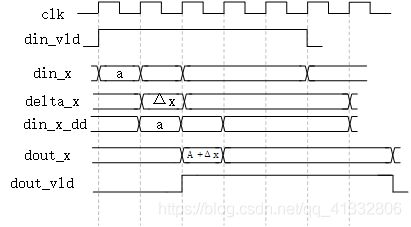
//----------------输入数据延时------------------
always @(posedge clk) begin
if (rst==1'b1) begin
pi_x_dd <= 'd0;
pi_y_dd <= 'd0;
pi_z_dd <= 'd0;
end
else begin
pi_x_dd <= pi_x;
pi_y_dd <= pi_y;
pi_z_dd <= pi_z;
end
end
//==========================================
// X(n + 1) = Xn - Sn * 2^(-n) * Yn
// Y(n + 1) = Yn + Sn * 2^(-n) * Xn
// Z(n + 1) = Xn - Sn * arctan(2^(-n))
//==========================================
//----------------计算输出和------------------
//1 clk
always @(posedge clk) begin
if (rst==1'b1) begin
po_x_r <= 'd0;
po_y_r <= 'd0;
po_z_r <= 'd0;
end
else begin
if (symbol == 1'b1) begin//Yn > 0; sn = -1
po_x_r <= pi_x_dd + delta_x;
po_y_r <= pi_y_dd - delta_y;
po_z_r <= pi_z_dd + delta_z;
end
else if (symbol == 1'b0) begin // sn = 1
po_x_r <= pi_x_dd - delta_x;
po_y_r <= pi_y_dd + delta_y;
po_z_r <= pi_z_dd - delta_z;
end
end
end
//----------------输出数据延时------------------
always @(posedge clk) begin
if (rst==1'b1) begin
po_dv_r <= 'd0;
po_data_info_r <= 'd0;
end
else begin
po_dv_r <= {po_dv_r[0], pi_dv};
po_data_info_r <= {po_data_info_r[1:0], pi_data_info};
end
end
endmodule
3.2.2 迭代处理核
完成了单个迭代处理单元后,需要进行16次迭代就相当于将上面的电路复制16份就可以了。
`timescale 1ns / 1ps
module cordic_core(
input wire clk ,
input wire rst ,
input wire pi_dv ,
input wire [19:0] pi_z ,//输入初始角度
input wire [19:0] pi_x ,//输入横坐标(归一化后的位宽)
input wire [19:0] pi_y ,//输入纵坐标(归一化后的位宽)
input wire [1:0] pi_data_info ,//保存坐标的象限信息
output wire po_dv ,
output wire [19:0] po_z ,//输出角度
output wire [19:0] po_x ,//输出横坐标(归一化后的位宽)
output wire [19:0] po_y ,//输出纵坐标(归一化后的位宽)
output wire [1:0] po_data_info //保存坐标的象限信息
);
//==========================================
//parameter define
//==========================================
parameter ITERATION_MAX = 16; //迭代最大次数
//==========================================
//internal signals
//==========================================
wire [19:0] din_x [16:0];
wire [19:0] din_y [16:0];
wire [19:0] din_z [16:0];
wire din_dv [16:0];
wire [1:0] din_data_info [16: 0];
generate
genvar i;
for (i = 0; i < ITERATION_MAX; i = i + 1)
begin:iteratior
cordic_unit #(
.ITERATION_IDX(i)
) inst_cordic_unit (
.clk (clk),
.rst (rst),
.pi_dv (din_dv[i]),
.pi_z (din_z[i]),
.pi_x (din_x[i]),
.pi_y (din_y[i]),
.pi_data_info (din_data_info[i]),
.po_dv (din_dv[i + 1]),
.po_z (din_z[i + 1]),
.po_x (din_x[i + 1]),
.po_y (din_y[i + 1]),
.po_data_info (din_data_info[i + 1])
);
end
endgenerate
assign din_dv[0] = pi_dv;
assign din_x[0] = pi_x ;
assign din_y[0] = pi_y;
assign din_z[0] = pi_z ;
assign din_data_info[0] = pi_data_info;
assign po_dv = din_dv[16];
assign po_x = din_x[16];
assign po_y = din_y[16];
//由于在第一象限中向x轴正方向旋转,因此得到的角度是负数
//需要求得角度的绝对值
assign po_z = ~din_z[16] + 1'b1;
assign po_data_info = din_data_info[16];
endmodule
3.4 相位信息复原模块

在迭代处理完成之后,可以认位当前已经移动到目标位置,此时,需要根据输入坐标存储好的相位信息,对原始数据的角度信息进行复原。同时在该模块中,还要对迭代模块中求得的模长进行校正,需要乘以一个模长校正因子。关于模长校正因子,对于16次迭代来所,其值约为0.60725 ≌ (1/2 + 1/8 - 1/64 - 1/512) - ((1/2 + 1/8 - 1/64 - 1/512)/4096);因此在进行模长校正时,也可以通过简单的移位和加法来完成。
`timescale 1ns / 1ps
module cordic_post(
input wire clk ,
input wire rst ,
input wire pi_dv ,
input wire [19:0] pi_z ,//输入初始角度
input wire [19:0] pi_x ,//输入横坐标(归一化后的位宽)
input wire [19:0] pi_y ,//输入纵坐标(归一化后的位宽)
input wire [1:0] pi_data_info ,//保存坐标的象限信息
output wire po_dv ,
output wire [19:0] po_angle ,//输出角度
output wire [19:0] po_amp //输出模长
);
//==========================================
//parameter define
//==========================================
//----------------角度常量,用于求得最终的角度信息------------------
localparam CONST_DOUBLE_PI = 20'h00000;//2π
localparam CONST_PI = 20'h80000;//π
localparam CONST_HALF_PI = 20'h40000;//π/2
//==========================================
//计算模长
//对于迭代16次的模长校正因子∏cosθ ≌ 0.607253
//采用流水线的方式,来进行长校正
//总共5个clk
//==========================================
//----------------输入数据右移------------------
//1 clk
reg [19:0] gain_tmp_r0 ;// >> 1
reg [19:0] gain_tmp_r1 ;// >> 3
reg [19:0] gain_tmp_r2 ;// >> 6
reg [19:0] gain_tmp_r3 ;// >> 9
always @(posedge clk) begin
if (rst==1'b1) begin
gain_tmp_r0 <= 'd0;
gain_tmp_r1 <= 'd0;
gain_tmp_r2 <= 'd0;
gain_tmp_r3 <= 'd0;
end
else begin
gain_tmp_r0 <= pi_x >> 1;
gain_tmp_r1 <= pi_x >> 3;
gain_tmp_r2 <= pi_x >> 6;
gain_tmp_r3 <= pi_x >> 9;
end
end
//----------------进行一次加法------------------
// tmp_r0 + tmp_r1;
// tmp_r2 + tmp_r3;
// 1 clk
reg [19:0] add_gain_r0 ;// gain_tmp_r0 + gain_tmp_r1
reg [19:0] add_gain_r1 ;// gain_tmp_r1 + gain_tmp_r2
always @(posedge clk) begin
if (rst==1'b1) begin
add_gain_r0 <= 'd0;
add_gain_r1 <= 'd0;
end
else begin
add_gain_r0 <= gain_tmp_r0 + gain_tmp_r1;
add_gain_r1 <= gain_tmp_r2 + gain_tmp_r3;
end
end
//----------------进行一次减法------------------
// add_gain_r0 - add_gain_r1
// 1 clk
reg [19:0] diff_gain_r0 ; // add_gain_r0 - add_gain_r1
reg [19:0] diff_gain_r0_dd ;
always @(posedge clk) begin
if (rst==1'b1) begin
diff_gain_r0 <= 'd0;
diff_gain_r0_dd <= 'd0;
end
else begin
diff_gain_r0 <= add_gain_r0 - add_gain_r1;
diff_gain_r0_dd <= diff_gain_r0;
end
end
//----------------进行一次移位------------------
// diff_gain_r0 >> 12
//1 clk
reg [19:0] gain_tmp_r4 ;// >> 12
always @(posedge clk) begin
if (rst==1'b1) begin
gain_tmp_r4 <= 'd0;
end
else begin
gain_tmp_r4 <= diff_gain_r0 >> 12;
end
end
//----------------得到输出结果------------------
//进行一次减法
// 1 clk
reg [19:0] diff_gain_r1 ;
always @(posedge clk) begin
if (rst==1'b1) begin
diff_gain_r1 <= 'd0;
end
else begin
diff_gain_r1 <= diff_gain_r0_dd - gain_tmp_r4;
end
end
//==========================================
//恢复角度,根据得到的象限信息恢复出原来的角度
//==========================================
// 1. 根据输入角度,判断当前角度是否处于第一象限
// 1 clk
reg [19:0] angle_abs ;
reg [1:0] data_info_dd0;
always @(posedge clk) begin
if (rst==1'b1) begin
angle_abs <= 'd0;
data_info_dd0 <= 'd0;
end
else if (pi_z[19] == 1'b1) begin
angle_abs <= ~pi_z + 1'b1;
data_info_dd0 <= pi_data_info;
end
else begin
angle_abs <= pi_z;
data_info_dd0 <= pi_data_info;
end
end
//2. 根据原始坐标的象限信息符号,确定角度
//1 clk
reg [19:0] angle_tmp;
always @(posedge clk) begin
if (rst==1'b1) begin
angle_tmp <= 'd0;
end
else begin
case(data_info_dd0)
//第一象限
2'b00 : begin
angle_tmp <= angle_abs;
end
//第4象限
2'b01 : begin
angle_tmp <= CONST_DOUBLE_PI - angle_abs;
end
//第二象限
2'b10 : begin
angle_tmp <= CONST_PI - angle_abs;
end
//第三象限
2'b11 : begin
angle_tmp <= CONST_PI + angle_abs;
end
endcase
end
end
//----------------po_dv_r, po_angle_r------------------
//po_dv_r 相较于输入,有5 clk的Latency
//po_angle_r 相较于angle-r 有 3 clk的Latency
reg [4:0] po_dv_r;
reg [59:0] po_angle_r ;
always @(posedge clk) begin
if (rst==1'b1) begin
po_dv_r <= 'd0;
po_angle_r <= 'd0;
end
else begin
po_dv_r <= {po_dv_r[3:0], pi_dv};
po_angle_r <= {po_angle_r[39:0],angle_tmp};
end
end
assign po_dv = po_dv_r[4];
assign po_angle = po_angle_r[59:40];
assign po_amp = diff_gain_r1;
endmodule
4 仿真结果
从测试结果来看,在上述Cordic实现的过程中的Latency为38,从数据输入到输出,共有38个时钟周期的延时

在仿真的时候,输入了几个测试点(112, 16), (-112,16), (-112, -16), (112, 16), (1, 3), (2, 2), (10, 10)
module tb_cordic_top (); /* this is automatically generated */
reg clk;
reg rst;
reg pi_dv;
reg [15:0] pi_x;
reg [15:0] pi_y;
wire [19:0] po_angle;
wire [19:0] po_amp;
wire po_dv;
integer i ;
cordic_top inst_cordic_top
(
.clk (clk),
.rst (rst),
.pi_dv (pi_dv),
.pi_x (pi_x),
.pi_y (pi_y),
.po_angle (po_angle),
.po_amp (po_amp),
.po_dv (po_dv)
);
// clock
initial begin
clk = 0;
forever #(5) clk = ~clk;
end
// reset
initial begin
rst = 1;
repeat (50) @(posedge clk);
rst = 0;
end
initial begin
pi_dv = 0;
pi_x = 0;
pi_y = 0;
@(negedge rst);
repeat(100) @(posedge clk);
gen_test_data();
end
task gen_test_data();
begin
repeat(10)@(posedge clk);
pi_dv = 1;
for(i = 0; i < 10; i = i + 1)begin
pi_x = 112;
pi_y = 16;
@(posedge clk);
pi_x = -112;
pi_y = 16;
@(posedge clk);
pi_x = -112;
pi_y = -16;
@(posedge clk);
pi_x = 112;
pi_y = -16;
@(posedge clk);
pi_x = 1;
pi_y = 3;
@(posedge clk);
pi_x = 2;
pi_y = 2;
@(posedge clk);
pi_x = 10;
pi_y = 10;
@(posedge clk);
end
pi_dv = 0;
end
endtask
endmodule
由于测试前几个测试点是照着《基于FPGA的数字图像处理》这本书上的,可以看到结果和书上一致,因此,确定Cordic工作正确,并且前4个点是各个象限中都有。
需要注意的是,输出的角度和模长都是经过量化后的,其中,输出的模长有4为小数位,经过验证,可以发现,当输入坐标越大时,实验得到的误差也就越小。

可以看到对于输入点(2,2),其输出结果是幅度20’h0002E,其中有4位小数位,可以计算出其值大为2.875,而2√2约为2.82842,输出的角度的量化值为20’h20068这与45°角的量化结果基本一致。
对于输入点(10, 10),其输出角度的量化值为20’h20068也基本等于45°。输出模长为20’h000e4,其值为14.375,而10√2约为14.1421。
总结
总的来说,Cordic算法的巧妙之处就是通过每次旋转固定的角度,不断迭代来达到目标旋转点的位置处。从而使使得FPGA不易实现的三角运算,变成了FPGA最擅长实现的移位,加法运算。
参考:《基于FPGA的数字图像处理》
1.基于FPGA的Cordic算法实现
2.CORDIC算法的FPGA实现