『区间DP』Polygon

题目描述

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.

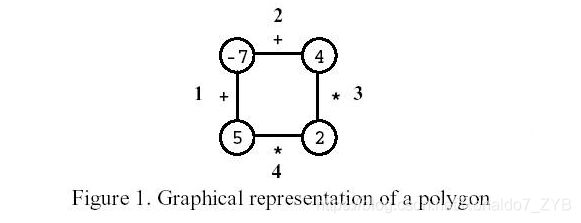
On the first move, one of the edges is removed. Subsequent moves involve the following steps:

1.pick an edge E and the two vertices V1 and V2 that are linked by E; and

2.replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.

The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

多边形游戏是一个单人玩的游戏，开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值，每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号 游戏第1步，将一条边删除 随后n-1步按以下方式操作 (1)选择一条边E以及由E连接着的2个顶点V1和V2 (2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点 最后，所有边都被删除，游戏结束。游戏的得分就是所剩顶点上的整数值

题解

这道题去掉一条边，只要将长度延长一倍，求每一个$[i,i+n-1](i\le n)$的答案即可。

如果数据仅仅为整数，我们可以直接进行区间DP，设$f[i][j]$表示区间$[i,j]$的最大值。

但是这里存在负数，很难进行最基本的状态转移，但是我们最大值和区间最大值和最小值息息相关。

例如，区间最大值有可能为：最大值+最大值；最小值 * 最小值；最大值 * 最大值。

区间最小值可能是：最大值 * 最小值；最小值+最小值；最大值 * 最大值；最小值 * 最小值。

解释一下最大值*最大值：$[-3,-2,-1]and[-6,-5,-4]$

代码如下：

#include 

#define int long long
#define Min(a,b,c,d,e) min(min(a,b),min(c,min(d,e))) 
#define Max(a,b,c) max(max(a,b),c)

using namespace std;
const int N = 200;

int n;
int a[N], op[N], f[N][N][2];

signed main(void)
{
	freopen("Polygon.in","r",stdin);
	freopen("Polygon.out","w",stdout);
	cin >> n;
	for (int i=1;i<=n;++i) 
	{
		char c;
		cin >> c >> a[i];
		op[i] = c == 'x' ? 1 : 0;
		//1 乘法 0 加法 
		a[i+n] = a[i], op[i+n] = op[i];
		f[i][i][0] = f[i+n][i+n][0] = f[i][i][1] = f[i+n][i+n][1] = a[i];
	}
	for (int len=2;len<=n;++len)
	    for (int i=1;i<=2*n-len+1;++i)
	    {
	        int j = i+len-1;
	        f[i][j][1] = -LONG_LONG_MAX, f[i][j][0] = LONG_LONG_MAX;
	        for (int k=i;k<j;++k) 
	        {
	        	if (op[k+1] == 1)
	        	{
	        		f[i][j][1] = Max(f[i][k][0]*f[k+1][j][0], f[i][k][1]*f[k+1][j][1], f[i][j][1]);
	        		f[i][j][0] = Min(f[i][k][0]*f[k+1][j][1], f[i][k][1]*f[k+1][j][0], f[i][k][0]*f[k+1][j][0], f[i][k][1]*f[k+1][j][1], f[i][j][0]);
	        	}
	        	if (op[k+1] == 0)
	        	{
	        		f[i][j][1] = max(f[i][k][1]+f[k+1][j][1],f[i][j][1]);
	        		f[i][j][0] = min(f[i][k][0]+f[k+1][j][0],f[i][j][0]);
	        	}
	        }
	    } 
	int ans = -LONG_LONG_MAX;
	for (int i=1;i<=n;++i) ans = max(ans, f[i][i+n-1][1]);
	cout<< ans << endl;
	for (int i=1;i<=n;++i) 
		if (f[i][i+n-1][1] == ans) cout<<i<<' ';cout<<endl;
	return 0;
}