状压dp小结

前言：博主是个很弱很弱的初学者，有错误欢迎大佬指出！

从铺砖块说起

Pro.现有n$\ast$m的一块地板，需要用1*2的砖块去铺满，中间不能留有空隙。问这样方案有多少种
Sol.这题应该每个人都做过吧qwq，这里用它引入介绍三种写法。

[下面的(i,j)竖放都是指覆盖(i,j)和(i-1,j)，为了方便直接写为竖放]

最普通的

因为在处理第(i+1)层时与前(i-1)层均已无关，所以很容易想到dp[i][j]表示处理到第i层，前(i-1)层已填满，第i层状态为j，其中j二进制下为1的第k位表示(i-1,k)竖放
转移为 $2^m$ 枚举i层填法，若合法则dp[i+1][k]+=dp[i][j]
初值dp[0][(1< 复杂度$O(n\ast n\ast 4^m)$

优化转移——去掉一些不合法状态的转移

容易发现上面的方法会有很多种不合法的转移
因为当(i-1,k)选择竖放时，(i,k)不可能再竖放。即二进制下(i-1)层状态为1的位，第i层的状态只能为0.
那么若只转到满足该条件的状态（注意这样也不一定合法，还是要判是否填满），设i层0的个数为k，则i层–>(i+1)层可能的转移数为$C_m^k\ast 2^k$
总转移数$\sum C_m^k\ast 2^k=(1+2{)}^m=3^m$
时间复杂度$O(n\ast n\ast 3^m)$

改变方向——从每个点的填法入手

如果继续沿用上面的状态，那么转移大概无法继续优化了吧qwq
我们考虑从每个点的填法入手，可以发现处理到(i,j)时，(i,j)的填法与(i-1,j)和(i,j-1)有关，而为了保证填满，我们还要记录这两点之间的所有点。

如图，太阳为处理到的点，钩为记录在状态内的点
那么dp[i][j][k]表示处理到(i,j)，k为(i,j)前m个点的状态(0,1意义不变)
设(i-1,j)为k中最低位，(i,j)的下一格为(x,y)，则转移为
1.$(i,j)$竖放 //且为了填满，此情况下只能竖放

if !(k&1) dp[x][y][(k>>1)+(1<<m-1)]+=dp[i][j][k] 

2.$(i,j)$横放 //注意若(i,j)为某一行第一格，不能横放

if !(k&(1<<m-1)) dp[x][y][((k^(1<<m-1))>>1)+(1<<m-1)]+=dp[i][j][k]

3.$(i,j)$不放

dp[x][y][k>>1]+=dp[i][j][k]

初值dp[1][1][(1< //假装第0层全为1初始化会方便很多呢
时间复杂度$O(n\ast m\ast 2^m)$

Code

//wy adorkable
#include
#include
#include
using namespace std;
inline int read()
{
	char ch=getchar(),last='!'; int ans=0;
	while (ch<'0'||ch>'9') last=ch,ch=getchar();
	while (ch<='9'&&ch>='0') ans=(ans<<3)+(ans<<1)+ch-48,ch=getchar();
	return (last=='-')?-ans:ans;
}
long long dp[15][15][10005];
int main()
{
	while (1)
	{
		int n=read(),m=read();
		if (n==0&&m==0) return 0;
		if (m==1){printf("%d\n",(n&1)?0:1); continue;}
		memset(dp,0,sizeof(dp));
		dp[1][1][(1<<m)-1]=1;
		for (int i=1; i<=n; i++)
			for (int j=1; j<=m; j++)
				for (int k=0; k<(1<<m); k++)
					if (dp[i][j][k])
					{
						int x=i,y=j+1;
						if (y==m+1) x++,y=1;
						//printf("dp[%d][%d][%d]=%d\n",i,j,k,dp[i][j][k]);
						if (!(k&1)) dp[x][y][(k>>1)+(1<<m-1)]+=dp[i][j][k];//,printf("1 --->dp[%d][%d][%d]=%d\n",x,y,(k>>1)+(1<>1)+(1<
						else 
						{
							if (j!=1&&!(k&(1<<m-1))) dp[x][y][((k^(1<<m-1))>>1)+(1<<m-1)]+=dp[i][j][k];//,printf("2 --->dp[%d][%d][%d]=%d\n",x,y,((k^(1<>1)+(1<>1)+(1<
							dp[x][y][k>>1]+=dp[i][j][k]; //printf("3 --->dp[%d][%d][%d]=%d\n",x,y,k>>1,dp[x][y][k>>1]);
						}     
						//puts("");
					}
		printf("%lld\n",dp[n+1][1][(1<<m)-1]);
	}
	return 0;
}

例题

例一 「NOIP2017」宝藏

LOJ#2318.「NOIP2017」宝藏

Pro.

选择并AK起点x。

若u已被AK，打通(u,v)可以使得v也被AK，代价为w(u,v)*已AK点构成的起点x至u路径的点数（包含x,u）

求使得所有点被AK的最小代价。

//由于adorkable语文过差，题面看起来很抽象，不过反正是NOIP题嘛应该都看过（逃

Sol.

容易发现题目其实是要求出一棵树使得所有点联通且边权和最小，因为边权和深度有关，
所以令dp[i][j]表示已选的点状态为i，当前深度为j。

转移$dp[k][j+1]=min(dp[k][j+1],dp[i][j]+j\ast \sum w(u,v))$。

若x在k中被选，i中未被选，那么x必须由i中某点的出边连接，所以答案一定合法。

若u在当前深度j被选而边(u,v)还未被打通但最终会被打通，那么v一定在深度(j+1)被选最优，所以答案不会偏大。

但是这样复杂度为$O(4^n\ast n^3)$

考虑优化。

可以发现若x在i中被选，在k中也一定被选，即k为x超集，那么时间复杂度优化为了$O(3^n\ast n^3)$（证明见上第二种方法

状态看起来不大容易继续优化了，但转移——计算选一些点的代价显然可以预处理

f[i][j]表示一个已选连通块i加入一个点j的代价 $O(2^n\ast n\ast m)$ //注意加入的点只能是某已选点出边直接连接的

g[i][j]表示一个已选连通块i选择一些点变为j的代价 $g[i][j]=\sum f[i][x]$ $O(3^n\ast n)$

那么$dp[k][j+1]=min(dp[k][j+1],dp[i][j]+g[i][k]\ast j)$; 就好辣

总复杂度$O(3^n\ast n)$

Code

//wy adorkable
#include
#include
#include
using namespace std;
inline int read()
{
	char ch=getchar(),last='!'; int ans=0;
	while (ch<'0'||ch>'9') last=ch,ch=getchar();
	while (ch<='9'&&ch>='0') ans=(ans<<3)+(ans<<1)+ch-48,ch=getchar();
	return (last=='-')?-ans:ans;
}
inline void chkmin(int &x,int y){x=(x>y)?y:x;}
inline void chkminll(long long &x,long long y){x=(x>y)?y:x;}
const int N=4505,M=2005;
int num,vet[M],val[M],nex[M],head[N];
int n,m,All,f[N][15];
long long ans,g[N][N],dp[N][15];
void add(int u,int v,int l)
{
	num++;
	vet[num]=v; val[num]=l; nex[num]=head[u]; head[u]=num;
}
int main()
{
	n=read(),m=read(),All=1<<n;
	num=0;
	for (int i=0; i<=n; i++) head[i]=-1;
	for (int i=1; i<=m; ++i)
	{
		int u=read()-1,v=read()-1,l=read();
		add(u,v,l); add(v,u,l);
	}
	//f-点到块 只能选直接出边
	for (int i=0; i<All; ++i)
		for (int j=0; j<n; ++j) f[i][j]=1e9;
	for (int i=0; i<All; ++i)
		for (int j=0; j<n; ++j)
			if ((i>>j)&1) 
				for (int e=head[j]; ~e; e=nex[e])
				{
					int v=vet[e];
					if (!((i>>v)&1)) chkmin(f[i][v],val[e]);
				}
	/*
	puts("f");
	for (int i=0; i
	//g-块到块
	for (int i=0; i<All; ++i)
		for (int j=i; j<All; j=(j+1)|i)
		{
			g[i][j]=0;
			for (int k=0; k<n; ++k) 
				if ((j>>k)&1&&!((i>>k)&1)) g[i][j]=g[i][j]+f[i][k];
		}
	/*
	puts("g");
	for (int i=0; i
	//dp[i][j]-打通了i状态，深度为j的最小代价
	for (int i=0; i<All; ++i)
		for (int j=0; j<=n; ++j) dp[i][j]=1ll<<60;
	ans=1ll<<60;
	for (int i=0; i<n; ++i) dp[1<<i][1]=0;
	for (int i=0; i<All; ++i)
		for (int j=1; j<n; ++j)
			for (int k=i; k<All; k=(k+1)|i) chkminll(dp[k][j+1],dp[i][j]+g[i][k]*j);
	for (int i=1; i<=n; i++) chkminll(ans,dp[All-1][i]);
	printf("%lld\n",ans); 
	return 0;
}

例二「CodePlus 2018 3 月赛」白金元首与莫斯科

LOJ6301.「CodePlus 2018 3 月赛」白金元首与莫斯科

Pro.

有一个$n\ast m$的格子，一些为空地一些为障碍，用$1\ast 2$的格子覆盖空地，可以不完全覆盖，求每个空地分别为障碍时覆盖方案数。

Sol.

有了前面的基础这题是不是就非常显然辣 /w\
首先不完全覆盖统计答案的时候会比较麻烦，那么其实不被覆盖的格子和障碍我们都可以想象成他们是被$1\ast 1$个格子填满了。但每个空地分别变为障碍怎么做呢，挺容易想到正着dp一遍倒着dp一遍吧，合并(i,j)的时候合法状态为(i-1,j)，(i+1,j)被覆盖，其余上下对应的格子状态一样(因为现在只能用跨线竖放的$1\ast 2$格子覆盖)

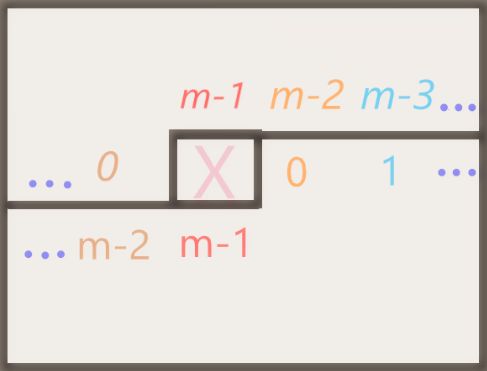
如图，X为当前变为障碍的空地，同色点状态相同，斜体为正着dp的状态，红色都为已覆盖
再大概地写一下dp过程好了
dp[i][j][k]表示处理到(i,j)，前m个点状态为k（以(i,j)的前一个为最高位，(i-1,j)为最低位）
(i,j)—>(x,y)
1.$(i,j)$竖放

dp[x][y][(k>>1)+(1<<m-1)]+=dp[i][j][k];

2.$(i,j)$横放

dp[x][y][((k^(1<<m-1))>>1)+(1<<m-1)]+=dp[i][j][k];

3.$(i,j)$不填

dp[x][y][k>>1]+=dp[i][j][k];

4.$(i,j)$填1*1

dp[x][y][(k>>1)+(1<<m-1)]+=dp[i][j][k];

然后要注意的是(i,j)是障碍的时候必须执行(4)，(i-1,j)为0时必须执行(1)，若矛盾则为不合法状态

Code

//wy adorkable
#include
#include
#include
using namespace std;
inline int read()
{
	char ch=getchar(),last='!'; int ans=0;
	while (ch<'0'||ch>'9') last=ch,ch=getchar();
	while (ch<='9'&&ch>='0') ans=(ans<<3)+(ans<<1)+ch-48,ch=getchar();
	return (last=='-')?-ans:ans;
}
const int N=20,P=1e9+7;
int a[N][N],f[(1<<17)+5],f1[N][N][(1<<17)+5],f2[N][N][(1<<17)+5];
inline void mo(int &x,int y){x=(x+y>=P)?(x+y-P):(x+y);}
int main()
{
	int n=read(),m=read();
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++) a[i][j]=read();
	f1[1][1][(1<<m)-1]=1;
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
			for (int k=0; k<(1<<m); k++)
				if (f1[i][j][k])
				{
					if (a[i][j]&&!(k&1)) continue;
					int x=i,y=j+1; if (y>m) x++,y=1;
					if (a[i][j]||!(k&1)){mo(f1[x][y][(k>>1)+(1<<m-1)],f1[i][j][k]); continue;}
					mo(f1[x][y][k>>1],f1[i][j][k]); mo(f1[x][y][(k>>1)+(1<<m-1)],f1[i][j][k]); 
					if (!(k&(1<<m-1))&&j!=1) mo(f1[x][y][((k^(1<<m-1))>>1)+(1<<m-1)],f1[i][j][k]);
				}
	f2[n][m][(1<<m)-1]=1;
	for (int i=n; i>=1; i--)
		for (int j=m; j>=1; j--)
			for (int k=0; k<(1<<m); k++)
				if (f2[i][j][k])
				{
					if (a[i][j]&&!(k&1)) continue;
					int x=i,y=j-1; if (y==0) x--,y=m;
					if (a[i][j]||!(k&1)){mo(f2[x][y][(k>>1)+(1<<m-1)],f2[i][j][k]);continue;}
					mo(f2[x][y][k>>1],f2[i][j][k]); mo(f2[x][y][(k>>1)+(1<<m-1)],f2[i][j][k]);
					if (!(k&(1<<m-1))&&j!=m) mo(f2[x][y][((k^(1<<m-1))>>1)+(1<<m-1)],f2[i][j][k]);
				}
	for (int i=0; i<(1<<m-1); i++)
	{
		int t1=(i<<1)+1; f[t1]=1;
		for (int j=0; j<m-1; j++) f[t1]=(t1&(1<<j+1))?(f[t1]+(1<<m-2-j+1)):f[t1];
	}
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++)
		{
			int ans=0;	
			if (!a[i][j]) 
				for (int k=0; k<(1<<m-1); k++) mo(ans,(long long)f1[i][j][(k<<1)+1]*f2[i][j][f[(k<<1)+1]]%P);
			printf("%d",ans);
			if (j==m) puts(""); else printf(" ");
		}
	return 0;
}