【ssl1338】人员分配【二分图】【最大匹配（模板）】【匈牙利算法】

Description

设有M个工人x1, x2, …, xm，和N项工作y1, y2, …, yn，规定每个工人至多做一项工作，而每项工作至多分配一名工人去做。由于种种原因，每个工人只能胜任其中的一项或几项工作。问应怎样分配才能使尽可能多的工人分配到他胜任的工作。这个问题称为人员分配问题。

Input

第一行两个整数m，n分别为工人数和工作数。
接下来一个整数s，为二分图的边数。
接下来s行，每行两个数ai,bi表示第ai个工人能胜任第bi份工作

Output

一个整数，表示最多能让多少个工人派到自己的胜任的工作上。

Sample Input

3 3
4
1 2
2 1
3 3
1 3

Sample Output

3

Hint

规模：
1<=m,n<=100
1<=s<=10000

分析&算法

求最大匹配的一种喜闻乐见 显而易见的算法是：先找出全部匹配，然后保留匹配数最多的。但是这个算法的复杂度为边数的指数级函数。因此，需要寻求一种更加高效的算法。

通过查找增广路，可以实现最大匹配。

由增广路的定义可以推出下述三个结论：

1. P的路径长度必定为奇数，第一条边和最后一条边都不属于M。
2. P经过取反操作可以得到一个更大的匹配M’。
3. M为G的最大匹配当且仅当不存在相对于M的增广路径。
   

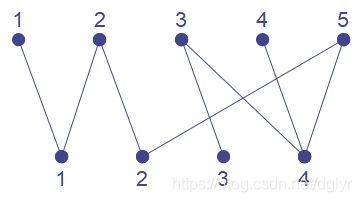
二分图就长上图这样。

算法轮廓：
(1)置M为空
(2)找出一条增广路径P，通过取反操作获得更大的匹配M’代替M
(3)重复(2)操作直到找不出增广路径为止

再说回这道题，就是匈牙利算法模板。

只要从每个点求增广路，往尽量多的点连一条链。如果碰到不行的就结束或者回溯。

增广路与匈牙利算法的专业解释如下：

增广路的定义(也称增广轨或交错轨)：
若P是图G中一条连通两个未匹配顶点的路径，并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。

求最大匹配常用匈牙利算法，它的基本思想是：对于已知的匹配M，从X中的任一选定的M非饱和点出发，用标号法寻找M增广链。如果找到M增广链，则M就可以得到增广；否则从X中另一个M非饱和点出发，继续寻找M增广链。
重复这个过程直到G中不存在增广链结束，此时的匹配就是G的最大匹配。这个算法通常称为匈牙利算法，因为这里介绍的寻找增广链的标号方法是由匈牙科学者Egerváry最早提出来的。

$Update:$这里附上很通俗易懂的匈牙利算法模拟：匈牙利算法

这道题我用了邻接矩阵和**邻接表(链式前向星)**两种方法存储。其实本质上是一样的，但是邻接表效率高一点。

上代码

邻接矩阵

#include
#include
#include
#include
typedef long long ll;
using namespace std;

int n,m,s,a[201][201],link[201],cover[201]; 

bool find(int x)
{
	for(int i=1;i<=m;i++)
	{
		if(a[x][i]==1&&cover[i]==0)
		{
			cover[i]=1;//记录走过 
			int q=link[i];//记录连边 
			link[i]=x; 
			if(q==0||find(q))//继续往下搜索 
			{
				return true;
			}
			link[i]=q;//回溯 
		}
	}
	return false;
}

int main()
{
    cin>>n>>m;
    cin>>s;
    for(int i=1;i<=s;i++)
    {
    	int x,y;
    	cin>>x>>y;
    	a[x][y]=1;//连边 
    }
    for(int i=1;i<=n;i++)
    {
    	memset(cover,0,sizeof(cover));
    	find(i);//每个点都搜一遍 
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
    	if(link[i]!=0) ans++;//统计已经匹配的答案 
    }
    cout<<ans;
	return 0;
}

邻接表（链式前向星）

#include
#include
#include
#include
typedef long long ll;
using namespace std;

int n,m,s,tot,ans,link[201],cover[201],hd[10001];

struct node
{
	int to,next;
}a[10001];

void add(int x,int y)
{
	a[++tot]=(node){y,hd[x]};
	hd[x]=tot;
}

bool find(int x)
{
	for(int i=hd[x];i>0;i=a[i].next)
	{
		int j=a[i].to;
		if(cover[j]==0)
		{
			cover[j]=1;
			int q=link[j];
			link[j]=x;
			if(q==0||find(q))
			{
				return true;
			}
			link[j]=q;
		}
	}
	return false;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
    	int x,y;
    	cin>>x>>y;
    	add(x,y);
    }
    for(int i=1;i<=n;i++)
    {
    	memset(cover,0,sizeof(cover));
    	find(i);
    }
    for(int i=1;i<=n;i++)
    {
    	if(link[i]!=0)
    	{
    		ans++;
    	}
    }
    cout<<ans;
	return 0;
}