计算机算法设计与分析--动态规划(二)
一、动态规划算法与分治法的区别
动态规划算法与分治法类似,其基本思想也是将待求解的问题分解成若干个子问题。但是,很多问题经分解得到的子问题往往不能互相独立。在用分治法求解时,有些问题被重复计算了多次。动态规划算法,对每一个子问题只解一次,而后将其解保存在一个表格中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果,从而获得较高的解题效率。
二、动态规划基本步骤
- 找出最优解的性质,并刻划其子结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解。
三、动态规划算法的基本要素
1、最优子结构性质
原问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
2、问题的重叠性质。
递归算法求解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。这种性质称为子问题的重叠性质。
3、备忘录方法。
备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
四、典型问题
1、完全加括号的矩阵连乘积
问题:给定n个矩阵A1、A2、…、An, 其中Ai与Ai+1是可乘的,i=1、2、…、n。
考察这n个矩阵的连乘积A1A2…An。
分析:将矩阵连乘积简记为A[i:j],这里i≤j。
(1)考察计算A[i:j]的最优计算次序:
设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,i≤k![]() 。
。
A[i:j]的计算量等于矩阵链A[i:k]的计算量加上矩阵链A[k+1:j]的计算量,再加上矩阵A[i:k]和矩阵A[k+1:j]相乘的计算量。
如果计算矩阵链A[i:j]的次序是最优的,那么必须计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。即,矩阵连乘积问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
(2)设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]。
当i=j时,A[i:j]=Ai,因此,m[i,i]=0,i=1,2,…,n
由于A[i:j]的计算量等于矩阵链A[i:k]的计算量加上矩阵链A[k+1:j]的计算量,再加上矩阵A[i:k]和矩阵A[k+1:j]相乘的计算量。
并且,矩阵链A[i:k]的最少计算量为m[i,k],矩阵链A[k+1:j]的最少计算量为m[k+1,j],矩阵A[i:k]和矩阵A[k+1:j]相乘的计算量为pi-1pkpj。
所以,当i

(3)掌握MatrixChain函数和Traceback函数
void MatrixChain(int p[num],int n,int m[num][num],int s[num][num])
{
for (int i = 1; i <= n; i++) m[i][i] = 0;
for (int r = 2; r <= n; r++)
for (int i = 1; i <= n - r+1; i++) {
int j=i+r-1;
m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k < j; k++) {
int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}
}
}
}
void Traceback(int i, int j,int s[num][num])
{
if(i==j)return;
Traceback(i,s[i][j],s);
Traceback(s[i][j]+1,j,s);
cout<<"Multiply A"<<i<<","<<s[i][j];
cout<<"and A"<<(s[i][j]+1)<<","<<j<<endl;
}
2、最长公共子序列
实现动态规划算法求给定2个序列X={x1, x2, …, xm}和Y={y1, y2, …, yn},找出X和Y的最长公共子序列。
(1)求两个序列的最长公共子序列
给定序列X={x1, x2, …, xm},则另一序列Z={z1, z2, …, zk}是X的子序列是指存在一个严格递增下标序列{i1, i2, …, ik}使得对于所有j=1,2,…,k有:zj=xij。例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。
给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。
(2)分析过程:
给定2个序列X={x1, x2, …, xm}和Y={y1, y2, …, yn},找出X和Y的最长公共子序列。
设序列Xm={x1, x2, …, xm}和Yn={y1, y2, …, yn}的最长公共子序列为Zk={z1, z2, …, zk} ,则
A. 若xm=yn,则zk=xm=yn,且Zk-1是Xm-1和Yn-1的最长公共子序列。即,求出Xm-1和Yn-1的最长公共子序列Zk-1={z1, z2, …, zk-1}之后,在Zk-1的后边加上zk,得到Zk= Z={z1, z2, …, zk},它就是X和Y的最长公共子序列。
B.若xm≠yn且zk≠xm,则Zk是Xm-1和Yn的最长公共子序列。
C.若xm≠yn且zk≠yn,则Zk是Xm和Yn-1的最长公共子序列。
注意:Xm=X={x1, x2, …, xm},Yn=Y={y1, y2, …, yn},Zk= Z={z1, z2, …, zk}
Xm-1={x1, x2, …, xm-1},Yn-1={y1, y2, …, yn-1},Zk-1={z1, z2, …, zk-1}
(3)建立递归关系
由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用c[i][j]记录最长公共子序列的长度。其中,Xi={x1, x2, …, xi};Yj={y1, y2, …, yj}。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。故此时C[i][j]=0。其它情况下,由最优子结构性质可建立递归关系如下:
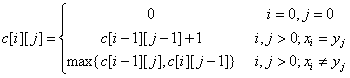
(4)掌握LCSLength 函数和LCS函数
void LCSLength(int m,int n,char x[],char y[],int c[N+1][N+1],int b[N+1][N+1])
{
int i,j;
for(i=0;i<=m;i++) c[i][0]=0;
for(i=0;i<=n;i++) c[0][i]=0;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
{
if (x[i-1]==y[j-1])
//A.若xm=yn,则zk=xm=yn,且Zk-1是Xm-1和Yn-1的最长公共子序列。
{
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1; //这是情况A
}
else if (c[i-1][j]>=c[i][j-1])
//B.若xm≠yn且zk≠xm,则Z是Xm-1和Y的最长公共子序列。
{
c[i][j]=c[i-1][j];
b[i][j]=2; //这是情况B
}
else
//C.若xm≠yn且zk≠yn,则Z是X和Yn-1的最长公共子序列。
{
c[i][j]=c[i][j-1];
b[i][j]=3; //这是情况C
}
}
}
void LCS(int i,int j,char x[],int b[N+1][N+1])
{
if (i==0 || j==0) return;
if (b[i][j]==1)
{
LCS(i-1,j-1,x,b);
cout<<x[i-1];
}
else if (b[i][j]==2)
LCS(i-1,j,x,b);
else
LCS(i,j-1,x,b);
}
3、凸多边形最优三角剖分问题
(1)问题
用多边形顶点的逆时针序列表示凸多边形,即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。
若vi与vj是多边形上不相邻的2个顶点,则线段vivj称为多边形的一条弦。弦将多边形分割成2个多边形{vi,vi+1,…,vj}和{vj,vj+1,…vi}。多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。
给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得即该三角剖分中诸三角形上权之和为最小。
(3)凸多边形的最优三角剖分问题有最优子结构性质:
事实上,若凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分T包含三角形v0vkvn,1≤k≤n-1,则T的权为3个部分权的和:三角形v0vkvn的权,子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。可以断言,由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。
(4)递推关系
事实上,若凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分T包含三角形v0vkvn,1≤k≤n-1,则T的权为3个部分权的和:三角形v0vkvn的权,子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。可以断言,由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。
设凸多边形{vi-1,vi,…,vj}的最优三角剖分的权为t[i][j],则原问题凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分的权为t[1][n-1]。
当i=j时,凸多边形退化为{vi-1 },t[i][j]=0。
当i
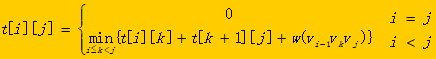
(3)掌握MinWeightTriangulation函数
void MinWeightTriangulation(int n,int t[num][num],int s[num][num])
{
for (int i = 1; i <= n; i++) t[i][i] = 0; //主对角线值为0
for (int r = 2; r <= n; r++)
for (int i = 1; i <= n-r+1; i++) {
int j=i+r-1;
t[i][j] = t[i+1][j]+ w(i-1,i,j);
s[i][j] = i;
for (int k = i+1; k < i+r-1; k++) { //扫描所有的剖分
int u = t[i][k] + t[k+1][j] + w(i-1,k,j); //求三部分的权之和
if (u < t[i][j]) { t[i][j] = u; s[i][j] = k;} //把最小的权存入t[i][j]
}
}
}
4、流水作业调度问题
(2)流水作业调度问题的Johnson算法
第一步:把作业的集合N={1,2,…,n}分为两个子集:N1和N2,令
第二步:将N1中作业依ai的非减序排序;将N2中作业依bi的非增序排序;
第三步:N1中作业接N2中作业构成满足Johnson算法的最优调度。
(3)掌握flowshop函数
void flowshop(int *a, int *b, int n, Job *N)
{
int i;
//由数组a、b建立数组N
for (i=0;i<n;i++)
{
N[i]=*(new Job(i+1,a[i],b[i]));
}
//建立数组N1、N2
Job *N1=new Job[n];
Job *N2=new Job[n];
//第一步:作业分组:把在机器1上处理时间小于在机器2上处理时间左右放到第一组N1,其它作业放到第二组N2。
int N1_num=0,N2_num=0;
for(i=0;i<n;i++)
{
if(N[i].getm1()<N[i].getm2())
{
N1[N1_num]=N[i];
N1_num++;
}
else
{
N2[N2_num]=N[i];
N2_num++;
}
}
//第二步:对数组N1、N2排序,对N1:按在机器1上加工时间的非减序(递增序)排序,对N2:按在机器2上加工时间的非增序(递减序)排序
sort1(N1,N1_num);
sort2(N2,N2_num);
//第三步:N1中作业接N2中作业合并到N
for(i=0;i<N1_num;i++)
{
N[i]=N1[i];
}
for(i=0;i<N2_num;i++)
{
N[N1_num+i]=N2[i];
}
delete N1,N2;
}
5、0-1背包问题(注意这是用动态规划算法解决0-1背包问题)
(1)问题:给定n种物品和一背包。物品i的重量是wi,其价值为vi,i=1、2、…、n。背包的容量为C。
问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
0-1背包问题是一个特殊的整数规划问题。 ![]()
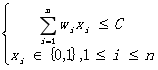
(2)分析:设所给0-1背包问题的子问题:从编号为i、i+1、…、n的物品中选择装入容量为j的背包的最优值(装入背包的物品价值和最大)为m(i,j),则 ![]()
上式是递推方程。
第一行表示第i个物品的重量小于背包的剩余容量j,这时候,物品i可以不装入背包(最优值),和装入背包(最优值![]() )。
)。
第二行表示第i个物品的重量大于背包的剩余容量j,这时候,物品i不能装入背包,只能继续考虑其余物品,从物品i+1开始考虑。
第n个物品的最优值是:
![]()
这是递推公式的边界条件。
(3)掌握Knapsack函数和Traceback函数
void Knapsack(int v[],int w[],int c,int n,int m[][mnum])
{
//cout<<"Knampsack"<
//填第n行
//注意m矩阵第n行表示第n个物品,第j列表示背包剩余容量j。
int jMax=min(w[n]-1,c);
for(int j=0;j<=jMax;j++)m[n][j]=0;
//第j列(背包剩余容量j)小于第n个物品重量,第n个物品不能装入背包。
for(j=w[n];j<=c;j++)m[n][j]=v[n];
//第j列(背包剩余容量j)大于第n个物品重量,第n个物品能装入背包。
//填第n-1行至第1行
for(int i=n-1;i>1;i--)
{
jMax=min(w[i]-1,c);
for(int j=0;j<=jMax;j++)m[i][j]=m[i+1][j];
//第j列(背包剩余容量j)小于第i个物品重量,第i个物品不能装入背包。
for(j=w[i];j<=c;j++)m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
//第j列(背包剩余容量j)大于第i个物品重量,第i个物品可以装入背包,也可以不装入背包,
//选择价值大的操作。
}
//考虑第1个物品
m[1][c]=m[2][c];//第1个物品不装入背包。
if(c>=w[1])m[1][c]=max(m[2][c],m[2][c-w[1]]+v[1]);
//比较第1个物品装入与不装入背包,选择价值大的操作。
}
void Traceback(int m[][mnum],int w[],int c,int n,int x[])
{
for(int i=1;i<n;i++)
{
if(m[i][c]==m[i+1][c]) x[i]=0;//第i个物品没有装入背包
else {x[i]=1;c-=w[i];}// 第i个物品装入背包
}
x[n]=(m[n][c])?1:0; //第n个物品装入背包
}