解读《视觉SLAM十四讲》,带你一步一步入门视觉SLAM—— 第 7 讲 视觉里程计1 ( 中 )
上一篇博客《解读《视觉SLAM十四讲》,带你一步一步入门视觉SLAM—— 第 7 讲视觉里程计1 ( 上 )》,我解读了特征点,讲述了关键点的提取和描述子的计算,以及特征点的匹配。经过匹配之后就会获得很多匹配点对。那么怎么从匹配的点对中获得相机的运动关系呢?
解读
对极约束
作者首先通过三点共面关系,推导出了对极约束。实际上这个推导过程还有一种更加简洁的方法,首先将书中对极几何约束示意图简化成如下形式:
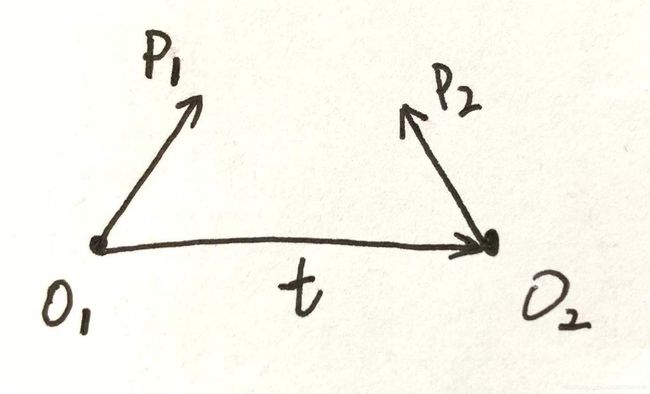
由于 O 1 p 1 , O 1 O 2 , O 2 p 2 O_1p_1,O_1O_2,O_2p_2 O1p1,O1O2,O2p2三者共面,所以可以得出下式:
O 1 p 1 ⃗ ⋅ ( O 1 O 2 ⃗ × O 2 p 2 ⃗ ) = 0 (0) \vec {O_1p_1} \cdot(\vec{O_1O_2} \times \vec{O_2p_2}) = 0 \tag 0 O1p1⋅(O1O2×O2p2)=0(0)上式采用书中的变量替换,则
p 1 ⋅ ( t ⋀ R p 2 ) = 0 (1) \boldsymbol p_1 \cdot(\boldsymbol t^{\bigwedge} \boldsymbol R \boldsymbol p_2) = 0 \tag1 p1⋅(t⋀Rp2)=0(1)注释:这里的 R p 2 \boldsymbol R \boldsymbol p_2 Rp2就是在 O 1 O_1 O1坐标系下表示 O 2 p 2 ⃗ \vec{O_2p_2} O2p2
是不是更好理解了,一个等式就得到了对极约束,通过一对匹配成功的特征点,我们可以得到一个对极约束,通过对极约束我们获得了非常重要的一个矩阵:本质矩阵 E = t ⋀ R \boldsymbol E =\boldsymbol t^{\bigwedge} \boldsymbol R E=t⋀R。
本质矩阵
本质矩阵有三个值得我们关注的地方:
- 1 对本质矩阵 E \boldsymbol E E乘以任意非零常数后,对极约束依然满足;
- 2 本质矩阵的奇异值必定是 [ σ , σ , 0 ] [\sigma,\sigma,0] [σ,σ,0];
- 3 本质矩阵实际上只有5个自由度。
五个自由度只需要五对匹配点就可以解出来本质矩阵,但是由于一些数学问题和便利性,常常采用8对点(这里的数学问题,我也不是很理解,大家可以参考相关文献[1][2])
根据对极约束,可以写出一对点的对极约束等式
[ u 1 , v 2 , 1 ] [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] [ u 2 v 2 1 ] = 0 (2) [u_1, v_2,1] \left[ \begin{matrix}e_1 & e_2 & e_3 \\ e_4 & e_5 & e_6 \\ e_7 & e_8 & e_9 \end{matrix} \right] \left[ \begin{matrix}u_2 \\ v_2 \\1\end{matrix} \right] = 0 \tag2 [u1,v2,1]⎣⎡e1e4e7e2e5e8e3e6e9⎦⎤⎣⎡u2v21⎦⎤=0(2)
根据八点法,只要有八组这样的方程,就可以解出对极约束中的本质矩阵 E E E。
八个方程,就算是满秩,解出9个变量,好像也是不太可能的,但是别忘记了,本质矩阵实际只有5个自由度。
根据八点法求得本质矩阵之后,通过SVD奇异值分解,可以得到 t , R \boldsymbol t,\boldsymbol R t,R,
《十四讲》中只是给了SVD分解的结论,至于中间过程,可以参考这篇博客《SVD分解(奇异值分解)求旋转矩阵》,求解出来的 t , R \boldsymbol t,\boldsymbol R t,R可以组成四种可能,此时需要通过正深度剔除另外三种情况。
单应矩阵
本质矩阵考虑的是空间中的任意组成的点集,但是实际在SLAM中有一些是特殊场景,比方说走廊或者墙面,所有的点都落在一个平面上了,此时如果还继续按照本质矩阵来求相机运动,就会导致退化问题,基础矩阵的自由度就会下降,此时多余出来的矩阵就由噪声来决定。所以为了解决这种问题,常常是同时计算本质矩阵和单应矩阵,然后选择重投影误差比较小的那个。
对于单应矩阵,书中首先根据平面表示公式:
n T P + d = 0 (3) \boldsymbol n^{T}P+d=0 \tag 3 nTP+d=0(3)实际上这个公式就是将我们高中的表示方法(4)式,采用向量的方法表示了:
A x + B y + C z + D = 0 (4) Ax+By+Cz+D=0 \tag 4 Ax+By+Cz+D=0(4)经过简单的推导(详细过程参考书本)就得到了,平面上的点在两个相机成像平面上的关系:
p 2 = K ( R − t n T d ) K − 1 p 1 (5) \boldsymbol p_2 = \boldsymbol K(\boldsymbol R- \frac{\boldsymbol t \boldsymbol n^{T}}{d})\boldsymbol K^{-1} \boldsymbol p_1 \tag5 p2=K(R−dtnT)K−1p1(5)将中间部分记为 H H H, H H H就叫做 单应矩阵,于是
p 2 = H p 1 (6) \boldsymbol p_2 = \boldsymbol H \boldsymbol p_1 \tag 6 p2=Hp1(6)对于单应矩阵的求解和本质矩阵是一样的套路,单应矩阵只需要四对匹配点就能求解得到,然后可以使用分解的方法求出 R \boldsymbol R R和 t \boldsymbol t t。分解之后同样也会面临四组解,也要通过一些约束进行排除。
尺度不确定性
在对极约束中,我们得到了本质矩阵 E = t ⋀ R \boldsymbol E =\boldsymbol t^{\bigwedge} \boldsymbol R E=t⋀R,试想一下如果我们给本质矩阵的 t \boldsymbol t t乘以一个常数 k k k, E = k t ⋀ R \boldsymbol E =k\boldsymbol t^{\bigwedge} \boldsymbol R E=kt⋀R,对极约束的关系依然成立。反过来讲,也就是当我们分解求 t , R \boldsymbol t,\boldsymbol R t,R时,就无法确定 t \boldsymbol t t的真实大小。
参考文献
R. I. Hartley, “In defense of the eight-point algorithm,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 6, pp. 580-593, June 1997. ↩︎
H.C. Longuet-Higgins,A computer algorithm for reconstructing a scene from two projections,Editor(s): Martin A. Fischler, Oscar Firschein,Readings in Computer Vision,Morgan Kaufmann,1987, ↩︎