1344 Knights 最大匹配

题目

We are given a chess-board of size nn, from which some fields have been removed. The task is to determine the maximum number of knights that can be placed on the remaining fields of the board in such a way that none of them check each other.
　　一张大小为nn的国际象棋棋盘，上面有一些格子被拿走了，棋盘规模n不超过200。马的攻击方向如下图，其中S处为马位置，标有X的点为该马的攻击点。

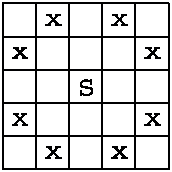
Fig.1: A knight placed on the field S checks fields marked with x.
Write a program, that:
reads the description of a chess-board with some fields removed, from the input file kni. in,
determines the maximum number of knights that can be placed on the chess-board in such a way that none of them check each other,
writes the result to the output file kni.out.
你的任务是确定在这个棋盘上放置尽可能多的马，并使他们不互相攻击。

题解

使用黑白染色法，把相邻的格子染成不同的颜色，可以发现，黑色格子只能攻击到白色格子而不能攻击到黑色格子
那么黑色格子和白色格子就可以看作是二分图的两部分，根据攻击规则给它们连边，每个格子赋予一个编号。求出最大匹配，则最大独立集=格子总数-最大匹配数-障碍格子=答案

时间复杂度$O(n^3)$

代码

#include 
#include 

using namespace std;

int n,m,ans,cnt,he,be;
int ls[20004],ne[200005],y[200005],link[20004];
bool cover[20004];
int e[204][204],f[204][204],c[20004],d[20004];
int x[10]={0,-2,-1,1,2,2,1,-1,-2};
int yz[10]={0,1,2,2,1,-1,-2,-2,-1};

bool dfs(int k){
	for (int i=ls[k];i;i=ne[i])
	if (!cover[y[i]]){
		int t=link[y[i]];
		link[y[i]]=k;
		cover[y[i]]=1;
		if (t==0||dfs(t)) return 1;
		link[y[i]]=t;
	}
	return 0;
}

int main(){
	scanf("%d%d",&n,&m);	
	for (int i=1;i<=m;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		e[a][b]=-1;
	}
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
		if (e[i][j]!=-1){
			if ((i+j)%2==0)
			{
				c[++he]=i;d[he]=j;
			}else f[i][j]=++be;
		}
	for (int h=1;h<=he;h++){
		int i=c[h],j=d[h];
		for (int l=1;l<=8;l++)
		if (i+x[l]>0&&i+x[l]<=n&&j+yz[l]>0&&
		j+yz[l]<=n&&f[i+x[l]][j+yz[l]]){
			cnt++;
			ne[cnt]=ls[h];ls[h]=cnt;y[cnt]=f[i+x[l]][j+yz[l]];
		}
	}
	for (int i=1;i<=he;i++){
		memset(cover,0,sizeof(bool)*(be+3));
		dfs(i);
	}
	for (int i=1;i<=be;i++)
		if (link[i]) ans++;
	printf("%d\n",n*n-ans-m);
}

阳光耀世紫荆正好，何不珍重今朝