【知识点总结】【CSP考前复习】图论大杂烩【未完】
序言
临近NOIP CSP-J 2019,不由得有些惆怅。
惆怅不是为了别的,主要是觉得从接触信息学竞赛开始,这已经是四个年头了,却一直拿的是二等奖。而今年是我最后的机会。如果不能成功,那自然就是AFO了。
一直想着应该做点什么,为我这么长时间的学习作个纪念,但一直没有想法也没有动力。
前不久,教练提出了专题复习的要求。听到这个建议,我觉得再好不过。将自己长时间来的学习经验作结,既是复习已知,也是将迷惑之处重新审视并解决的大好机会。
如果最后能走向成功,那就归功于这成功的复习;
但如若未能成功,那至少,我也留下了独一无二的东西,属于我自己的东西。
这些知识点大概会由两部分组成,一部分是我跟这个算法的故事,不感兴趣可以自行跳过,当然当成小说看看也无妨(其实多少都没有);另一部分是我对这个算法的理解运用以及一些经典的例题(都来自氵谷和校内平台)。
仅以这些复习性的文章,纪念我四年的OI生涯。
目录:
一、X短路的那些事
1、人生苦短,时间有限,劝君更惜少年时—最短路算法
2、该打的仗,我打尽了;该走的路,我走遍了——K短路
二、数学化の图论
1、关于意义之塔的塔顶,不要去想,因为可能没有塔顶——拓扑排序
2、温故而知新,回归本质,能发现不一样的世界——差分约束
三、绕来绕去那些事——环上问题
1、强联通,点双,边双
2、负环
3、欧拉回路,哈密尔顿回路
4、EX:某些特殊的环上问题
四、螺旋升天,生成树法力无边——生成树问题
1、最小/最大生成树——Prim & Kuskal
------后面待填坑.jpg------
2、最小乘积生成树
3、最小树形图
4、EX:关于最小生成树在LCT中的运用
5、EX:关于生成树为啥这么好用
五、凑上一对是一对——二分图匹配问题
1、Edmond_Karp-最初算法
2、Dinic&Isap-逐渐进步
3、HLPP-最高标号预流推进
4、看不出来的网络流—无源汇、可行流、上下界
5、暴力出奇迹,问题是怎么暴力—建图模型
6、逻辑命题判对错——2-SAT
7、EX:LCT在处理动态二分图中的运用
六、一些有趣的思考
1、边点互换,点化边&边化点
2、时光倒流,删除变更新
3、建立虚点,避免无用操作
4、最小割转最短路,平面图转对偶图
5、最长反链与最小链覆盖
一、X短路的那些事
1、人生苦短,时间有限,劝君更惜少年时———最短路算法
时间回到2017年,NOIP2017普及组考试赛场上。
面对T3发懵的我,虽然没有学BFS,却用草稿纸和笔模拟了BFS的整个过程。(尽管最后还是没分)
这是我第一次接触搜索算法。然而当时的我没有意识到,搜索算法将会陪伴我整个OI生涯。
从最最基础的走迷宫,到迭代加深、折半搜素等巧妙的操作,再到面对难题时必不可少的找规律骗分,靠的都是搜索及其衍生。搜索作为一种基础算法,进化方向之多,从图论到数据结构再到DP都能看见它的影子。
时间有限,篇幅有限,我们在这里只扯一扯图论上的搜索。
搜索贯彻的概念是:遍历所有状态,收集所有信息,然后我们从中提取我们需要的信息作为服务。
那么我们面临的一类问题:最短路问题,可以用搜索轻松的解决。但是,单纯的搜索势必有着效率低下的问题,我们需要考虑一些改进,使得效率更加优秀。
由神仙zxy所说,效率的改进最主要体现在我们利用最有价值的信息而抛弃不用的信息,选取有用的更新而抛弃无用的转移,从而达到简化程序的目标,是优化程序运行速率的方法之一
于是,我们有了最短路界的三大算法:Floyd,Dijkstra,SPFA
P3371 单源最短路径(弱化版)
Floyd
OI界一个普遍的规律就是:一个算法与同种的其他算法相比,复杂度越高,往往就更容易理解。O(N^3)的效率注定了Floyd浅显易懂&平易近人。
不过,Floyd其实是基于DP而非搜索的思想,也算是个特例。
但这并不代表Floyd是个不优秀的算法,毕竟一轮Floyd就能处理出每两个点之间的最短路距离:
inline void Floyd()
{
for(int i=1;i<=n;i++){
for(rint k=1;i<=n;k++){
for(rint j=1;j<=n;j++){
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j];
//核心思想:考虑以每个点作为中转点,更新另外两点的最短距离
//其实也就是枚举这个点是否在另两个点的最短路上
//O(N^3)的枚举是保证信息正确性的基础
}
}
}
}
经典的例题是P1119 灾后重建,在这道题中Dij和SPFA都没法做到快速的动态更新,但Floyd就可以了。
Dijkstra
Dijkstra则是平时用的最多的最短路算法。朴实的Dij运行效率O(N^2),因此各路大佬想出了各种玄学优化,比如线段树优化,zxy神仙的vector+set优化,当然最广为人知的还是优先队列优化的版本:
typedef pair<int,int> pii;
priority_queue<pii,vector<pii>,greater<pii> >q;
inline void Dijkstra()
{
for(int i=1;i<=n;i++)vis[i]=0,dis[i]=0x3f3f3f3f;
dis[1]=0;q.push(make_pair(0,1));
while(!q.empty()){
int now=q.top().second();q.pop();
if(vis[now])continue;
vis[now]=1;
for(int i=head[now];i;i=e[i].nxt){
int d=e[i].v;
if(dis[d]>dis[now]+e[i].w){
dis[d]=dis[now]+e[i].w;
q.push(make_pair(dis[d],d);
}
//核心思想:利用堆的性质每次取最小值更新
//每当一个点被更新就丢进去更新别人
//效率是O(mlogN)
}
//不过现在我貌似不打这个……
Dij的致命缺陷是:应对不了负边权的情况。一旦有负边权,我们的贪心本源,即(更新之后的答案一定大于当前答案)这点就错了,自然Dij也就GG了。(好像有什么玄学方法可以跑负权图,有空我去学学)
例题的话就不找了,毕竟Dij处处可见。就放一下初见:P1339 热浪
SPFA(它死了)
SPFA(Shortest Path Faster Algorithm),效率是玄学复杂度O(KM),遇到毒瘤数据是可以卡成O(NM)的
比如P4779 单源最短路径(加强版)和NOI2018 D1T1 归程
不过SPFA的优越体现在它可以解决负边权的情况,因此除了跑最短路,它还可以判负环。
queue<int> q;
inline void SPFA()
{
for(int i=1;i<=n;i++)dis[i]=inf;
q.push(1);
while(!q.empty())
{
int now=q.front();q.pop();
in[now]=0;
for(int i=head[now];i;i=h[i].nxt)
{
int d=e[i].v;
if(dis[v]>dis[u]+h[i].w)
{
dis[v]=dis[u]+h[i].w;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
//有趣的一点是长得很像Dij
//因此Dij也可以写成这个样子
}
运用是P3385 【模板】负环。(下面还有讲)
小结
最短路算法可以说是我重新开始的起点。
高一暑假的我重拾信竞从头追赶,最短路是我第一个接触到的。当时的我为这种神奇的思想深深叹服,同时更添一份对信息学的热情。
一年过去了,我认识了更多神奇的算法,在复杂的数据结构中挣扎过多个白天,也在精妙的DP中辗转数个夜晚。然而当我回首,最短路算法仍然给我感动,因为那是最初的感动。
正如那句话:TLE之前,没有任何一个节点叫做失败。
最短路算法是图论中最基础的东西。其实所谓的难题,都是有许多这样的基础,以及一点点的灵机一动拼凑而成。所以这基础中的基础,必须要好好掌握。
衍生
常见的变式(我见过的)有这些:
1、P1144 最短路计数 建立在求最短路基础上的DP。
2、P2149以及校内测试 规避和校内测试 图Graph等 双起点双终点以及最短路交集的一类问题
关键性质:两条最短路相交的部分一定为连续的一段
3、最短路树&最短路DAG,前者往往用的更多,因为有树形结构嘛。比如校内测试 困难的图,等等(主要是找不到了 )。
关键性质:最短路树上只有返祖边,利用最短路树的性质进行DP,树上差分等统计一些信息(比如环的个数,K短路个数)
2、该打的仗,我打尽了;该走的路,我走遍了——K短路
总有那么一些与众不同的人,他们卓尔不群,剑走偏锋,跳脱于大众之外,从人们的习以为常中发现新的可能。
从最短路到K短路,从A*到可持久化左并堆,哪怕是今天,许多算法的效率还在提升之中
我对这些执着于追求“更好”的人,致以崇高的敬意、
K短路问题的解决自然可以用最短路多跑几遍得到,但面临的问题还是效率低下。那么随之衍生的就有两种方案:
A*
A*可以说是简单易懂好上手的算法了,只需要在原有Dijkstra的基础上加上一份估价函数,这份最短路代码就能跑出K短路来。
具体操作,就是先从终点反向来一遍最短路,以每个点的反向dis值+正向dis值为估价函数,使得第K个到达终点的路径就是第K短的路:
不过,A*的效率不敢保证,虽然存在把加边顺序打乱可以飞快地玄学说法 ,复杂度毕竟还是要根据图来。
那么在这时,有一种更加稳定高效的方法——可持久化可并堆就出现了。
可持久化可并堆
可并堆:又称左偏树,一个具有左偏性质的堆,可以logn支持两个堆合并。
可持久化可并堆:顾名思义,每次新开节点搞事即可
那么这怎么解决K短路呢?这里我选择zxy神仙的完美论述(我自认为说不了这么好):
首先我们想一想为什么A_*跑得慢 ?
因为最短路有相当多的信息可以利用,但是A_*只利用了距离来做估价函数。
现在考虑怎么得到一个不是那么短的路,接下来将“不那么短的路”称为欠短路径。
我们已经求出了最短路了。也就是说,我们至少现在又最短路树和最短路DAG可以利用。
我们选择结构更为简单的最短路树。构建出任意一棵最短路树,树根为T。
然后剩下一些非树边。考虑任意一条非树边,我们从S走到v后再走到w显然就能得到一条欠短路径。
所以我们考虑所有合法的非树边的序列,我们只需要将这个这个序列中的第K小找出来就行了。
(看完给我一种茅塞顿开的感觉,我相信你们也是)
这样一来问题就简单化了,说明如下:
1、反向跑最短路建出最短路树。
2、利用可持久化可并堆构建出(每个节点到根节点路径上返祖边)小根堆。
3、从起点开始跑最短路,扩展结点的方式是走比当前边大一点点的返祖边或者走树边。
(代码实现之后补)
这个算法的复杂度稳定在
小结
许多人学习了A*之后,即使听说有这么一个更高效更稳定的算法,也没有兴趣再学
毕竟只在某一个问题上,为了小概率的被卡而学习另一种更复杂的方法,不是什么划算的事
但我认为学习从来就不是什么划不划算的问题
我所学到的,到头来都是自己的东西,这怎么看都稳赚不赔
能多学一点就多学一点,这才是我学习OI的初衷吧?
二、数学化の图论、
1、关于意义之塔的塔顶,不要去想,因为可能没有塔顶——拓扑排序
拓扑排序代码难度低,思维难度低,算是我遇到过的为数不多的用的广学得快的算法之一。
针对一个有向无环图,我们利用拓扑排序可以给每个点分好一个高度/深度,从而建立出类似A>B,C>B的这些关系构成图。得到的深度相同的一组,就可以任意取值,否则就要满足深度之间的不等关系。
inline void addedge(int u,int v)
{
e[++cnt]=(Edge){v,head[u]},head[u]=cnt;
in[v]++;
}
queue<int>q;
inline void Topological_sort()
{
for(int i=1;i<=n;i++)if(!in[i])q.push(i);
while(!q.empty()){
int now=q.front();q.pop();
for(int i=head[now];i;i=e[i].nxt){
int d=e[i].v;
deep[d]=max(deep[d],deep[now]+1);//根据情况也可能是min
if(!--in[d])q.push(d);
}
}
}
拓扑排序多用于处理逻辑关系,P1983 车站分级是一个很经典的例子。
另外,在博弈论当中,拓扑排序也可以完成胜负状态之间的建图以及转移,不过往往还需要搭配Tarjan使用。
题我实在懒得找了反正就是有
2、温故而知新,回归本质,能发现不一样的世界——差分约束
那天我看到一道关于不等式的题,一脸懵逼:这还能怎么做?
打开题解一看:???Dijkstra是什么玩意儿??
然后愣了几秒突然醒悟:原来是根据性质定义来的啊
那一刻我觉得,是不是还有很多基本的算法,可以运用到更多的地方去
只是我们还没有发现吧?
差分约束是为了满足类似于a>=b,c<=d等一系列式子,并构造出一组合法解的算法。它的巧妙之处在于利用了最短路的一个性质,即在无负权的图里面,dis[v]<=dis[u]+e[i].w。
于是,我们就可以转化啦。比如a<=b,我们就从b往a连边权为0的边。以此类推。
(code就不放了,太简略了.jpg)
其实差分约束的题不算特别多,我有印象的只有P1993 小K的农场…而且好像已经很久没看到以差分约束为考点的题了。但是这种探寻本质从而解决新问题的思路,值得学习。
三、绕来绕去那些事——环上问题&回路
1、Tarjan三重奏
Tarjan老爷子是我很佩服的人之一
先不说这个有向无向都可用的tarjan算法
创造LCT并且为了证明复杂度顺便开发了SPLAY这件事已经很NB了
Tarjan三重奏是针对有向图中强连通分量,无向图中割点、割边的一类算法,根据所求对象不同代码也有微调:
//核心思想:
//dfn记录第一次到这个点时的时间
//low记录从这个点出发能到达的最小时间
ivoid tarjan_strong_connect(int x)//1.强连通分量-有向图
{
dfn[x]=low[x]=++cnt;
dl[++tot]=x;
vis[x]=1;
for(rint i=head[x];i;i=edge[i].next){
if(!dfn[edge[i].v]){
tarjan_strong_connect(edge[i].v);
low[x]=min(low[x],low[edge[i].v]);
}
else if(vis[edge[i].v]){
low[x]=min(low[x],dfn[edge[i].v]);
}
}
if(dfn[x]==low[x]){//它最多能到自己,那就是强连通
vis[x]=0;
while(x!=dl[tot+1]){
cout<<dl[tot]<<" ";
vis[dl[tot]]=0;
tot--;
}
cout<<"is a strongly connected component"<<endll;
}
}
int node_biconnect[N];
void tarjan_node_biconnect(int x)//2、无向图-割点
{
int son=0;
low[x]=dfn[x]=++cnt;
for(rint i=head[x];i;i=edge[i].next){
int d=edge[i].v;
if(!dfn[d]){
son++;
fa[d]=x;
tarjan_node_biconnect(d);
low[x]=min(low[x],low[d]);
if(low[d]>=dfn[x]&&fa[x])//它的孩子不能到比他高的地方,那就是割点
node_biconnect[x]=1;
}
low[x]=min(low[x],dfn[d]);//这里注意与缩点不同,用的是dfn
}
if(fa[x]==0&&son>=2)//特判根节点
node_biconnect[x]=1;
}
typedef pair<int,int> pmc;
queue<pmc> edge_biconnect;
iint tarjan_edge_biconnect(int x)//无向图-割边
{
int lowx=0,lowy=0;
low[x]=dfn[x]=++cnt;
for(rint i=head[x];i;i=edge[i].next){
if(!dfn[edge[i].v]){
fa[edge[i].v]=x;
lowy=tarjan_edge_biconnect(edge[i].v);
lowx=min(lowx,lowy);
if(lowy>dfn[x])//特别注意这里与割点不同之处
edge_biconnect.push(make_pair(min(u,v),max(u,v)));
}
else{
if(edge[i].v!=fa[x]&dfn[edge[i].v]<dfn[x])
lowx=min(lowx,dfn[edge[i].v]);
}
}
low[x]=lowx;
return lowx;
}
关于其作用我们一个一个分析:
强连通分量:常见于有向图中拿来缩环成点,方便统计计算
避免你跑dfs啊最短路啊什么的时候掉到环里挂掉
当然还可以搭配圆方树使用跑仙人掌
割点:这个真的见得不多,除了模板题会用我真是没怎么见过……
割边:我所知的用法之一是在基环树中用,以此判断哪些边处于基环上但同样都是O(N)为什么我不直接枚举断边emmmm。
反正这一家子真要用的时候应该都是能轻松看出来的,但并不意味着它们出现的题就会很简单,比如我出到树上套几个数据结构什么的你试试。
因为我太懒了所以例题之后找反正应该都很简单
2、负环
虽然前面已经提到过了不过还是想再说一下。
SPFA判负环的格式有两种:DFS版和BFS版。
DFS版是看有没有遇到已经入队的点,有则是存在负环,原理是如果一个点在最短路上出现多次就是出现了负环。
BFS版是看每个点的入队次数,根据最短路性质,每个店入队肯定不会超过n次,所以入队次数>=n就说明有负环。
两种算法好像都有自己的局限性,反正氵谷上的毒瘤数据卡死了DFS,那估计BFS是要好一点?
iint spfa()
{
queue<int>q1;
memset(dis,0x3f,sizeof(dis));
memset(visited,0,sizeof(visited));
memset(vis,0,sizeof(vis));
dis[1]=0;q1.push(1);
while(!q1.empty()){
int now=q1.front();q1.pop();
vis[now]=0;
for(rint i=head[now];i;i=edge[i].next){
int d=edge[i].v,w=edge[i].w;
if(dis[d]>dis[now]+w){
dis[d]=dis[now]+w;
if(!vis[d]){
if(++visited[d]>=n)return true;
vis[d]=1;q1.push(d);
}
}
}
}
return false;
}
用处emmmmm我是真不知道+1,估计也是特殊情况下用来预处理图以方便跑别的算法的吧?
3、欧拉回路 & 哈密尔顿回路
欧拉回路:经过图中每条边恰好一次的路径。
结论:
①无向图G存在欧拉通路的充要条件是:图为连通图,并且该图仅有两个奇度结点(度数为奇数的顶点)或者无奇度结点。
②有向图D存在欧拉通路的充要条件是:D的基图连通(基图指有向图不管每个点的方向形成的无向图),并且所有顶点的出度与入度相等;或者,除两个顶点外,其余顶点的出度与入度都相等,而这两个顶点中一个顶点的出度与入度之差为1,另一个顶点的出度与入度之差为-1。
解决方式:在加边的时候判断下充要条件,找出合适的起点,然后跑跑dfs,复杂度 O ( N + M ) O(N+M) O(N+M)。
哈密尔顿回路:经过图中每个点恰好一次的路径。
这个东西最近好像没提出什么有用的充要条件,只提出了不少充分条件,感兴趣的话可以去自行了解一下,这里不多做讲解。
这两个东西考的也比较少,不过不排除利用其性质出一些奇怪的题的可能。
说白了就是我题做得少没见过
4、EX:某些特殊的环上问题
上述算法都是因为存在环所以能实施,实际上在有些问题中,会有环的形成,但我们并不把环加到图里面,而是通过一些另外的操作来记录这些环,同时保证一棵树的结构。
比较常见的是用在生成树上的时候,往往为了动态维护还需要搭配LCT,这类题很多,普通一点的如P2542 航线规划和P4172 水管局长,还有个间接维护二元属性的P2387 魔法森林,以及维护二分图的BZOJ4025 二分图(校内链接),说起来都是一类动态维护生成树,并判断生成树上环的问题,非常经典。
我这里写这么多以后复习数据结构我又写啥呢emmmm
四、螺旋升天,生成树法力无边——生成树问题
1、最小/最大生成树——Prim&Kruskal
之所以说是最小/最大是因为改改排序就能实现了
关于最小生成树的定义:在无向图中找到一颗生成树,使得这颗生成树上的边权的最大值最小。
听到最小我们自然而然开始想贪心。那么由于哲学问题 "先选边还是先选点?"的出现,我们进行了不同的尝试,最终产生了以选点为基础的Prim算法和以选边为基础的Kruskal算法:
//Prim:随机选一个点并塞入队列,每轮取一个点,把与这个点相邻的所有还未入队的点加入。
//队列按照(与已经取出的点的最近距离)为关键字从小到大排序。
//实现上有点像Dij,毕竟思想差不多
//这是朴素的Prim
ivoid Prim()
{
for(rint i=1;i<=n;i++)dis[i]=inf,vis[i]=0;
for(rint i=head[1];i;i=e[i].nxt){
dis[e[i].v]=min(dis[e[i].v],e[i].w);
}
int now=1;
while(++tot<n){
int mn=inf;vis[now]=1;
for(rint i=1;i<=n;i++){
if(!vis[i]&&mn>dis[i]){
mn=dis[i],now=i;
}
}
ans+=mn;
for(rint i=head[now];i;i=e[i].nxt){
rint d=e[i].v;
if(dis[d]>e[i].w&&!vis[d])dis[d]=e[i].w;
}
}
}
//这是堆优化的Prim
typedef pair<int,int>pii;
priority_queue<pii,vector<pii>,greater<pii> >q;
ivoid Prim()
{
for(rint i=1;i<=n;i++)dis[i]=inf,vis[i]=0;
dis[1]=0;q.push(make_pair(0,1));
while(!q.empty()&&tot<n){
int val=q.top().first,now=q.top().second;
q.pop();if(vis[now])continue;
vis[now]=1;tot++;ans+=val;
for(rint i=head[now];i;i=e[i].nxt){
int d=e[i].v;
if(e[i].w<dis[d])
q.push(make_pair(dis[d]=e[i].w,d));
}
}
}
//Kruskal:把所有边按权值从小到大排序,枚举每一条边
//如果连接的两个点已经处于同一个连通块就不管
//否则并查集合并,ans+
//由于是从小到大贪心去因此可以保证正确性
int fa[N];
iint find(int x){return (x==fa[x])?(fa[x]):(fa[x]=fa[fa[x]]=find(fa[fa[x]]));}
inline bool operator <(const Edge &q1,const Edge &q2){return q1.w<q2.w;}
ivoid Kruskal()
{
sort(e+1,e+cnt+1);
for(rint i=1;i<=n;i++)fa[i]=i;
for(rint i=1;i<=cnt;i++){
int x1=find(e[i].u),x2=find(e[i].v);
if(x1!=x2){fa[x1]=x2;ans+=e[i].w;tot++;}
if(tot==n-1)break;
}
}
堆优化后的这个Prim效率是 O ( N l o g N ) O(NlogN) O(NlogN),
没有堆优化的一般形式Prim是 O ( N 2 ) O(N^2) O(N2),
而Kruskal的复杂度是 O ( M l o g M ) O(MlogM) O(MlogM)。
根据两种算法的实现就能大致看出:
1、Prim在稠密图中的效率比Kruskal好,但是在稀疏图中就不如Prim。
2、尽管堆优化的Prim效率很好,但是当图过于稠密的时候会因为内存过大而emmmm。
所以还是要根据实际的题目选择适当的算法,防止毒瘤出题人恶意卡常……
在最小生成树的基础上稍稍拓展一下,就可以得到严格/非严格次小生成树,也就是 O ( M ) O(M) O(M)把每一条边扫一次,然后假设强行加入并去除加入后形成的环上除该边外的最大边,就可以得到次小生成树.jpg
2、最小乘积生成树
有这么一类问题:对于一个无向图,每条边有两个权值 a i ai ai, b i bi bi,需要你求出一颗生成树,使得最终的 a i ai ai之和与 b i bi bi之和的乘积最小。解决这类问题就需要用到最小乘积生成树。
解决方案如下:
(借鉴于这个大佬的博客)
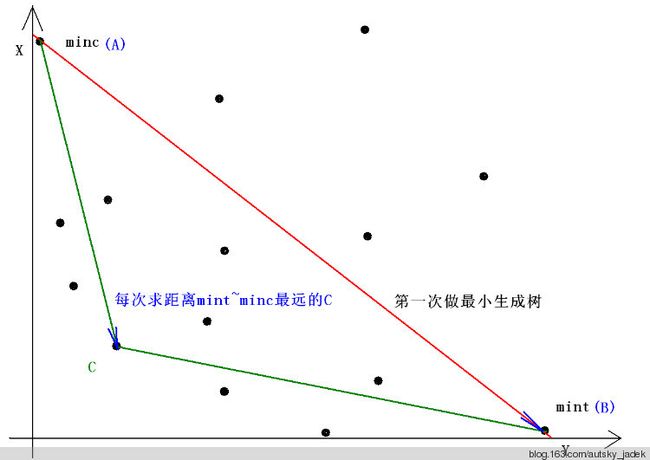
我们建立一个平面直角坐标系,每个点对应一种方案,横坐标为 a i ai ai之和,纵坐标为 b i bi bi之和。
那么题目就是让我们最小化这个点和原点构成的矩形的面积,步骤如下:
1、求得分别距x轴和y轴最近的点:A、B(分别按x权值和y权值做最小生成树即可)。
2、:寻找一个在AB的靠近原点一侧的且离AB最远的生成树C,试图更新答案。
R e a s o n : Reason: Reason:由于C离AB最远,所以S△ABC面积最大。
向量 A B = ( B . x − A . x , B . y − A . y ) AB=(B.x - A.x , B.y - A.y) AB=(B.x−A.x,B.y−A.y)
向量 A C = ( C . x − A . x , C . y − A . y ) AC= (C.x - A.x , C.y - A.y) AC=(C.x−A.x,C.y−A.y)
向量AB、AC的叉积(的二分之一)为S△ABC的面积(只不过叉积是有向的,是负的,所以最小化这个值,即为最大化面积)。
最小化: ( B . x − A . x ) ∗ ( C . y − A . y ) − ( B . y − A . y ) ∗ ( C . x − A . x ) (B.x-A.x)*(C.y-A.y)-(B.y-A.y)*(C.x-A.x) (B.x−A.x)∗(C.y−A.y)−(B.y−A.y)∗(C.x−A.x)
= ( B . x − A . x ) ∗ C . y + ( A . y − B . y ) ∗ C . x − A . y ∗ ( B . x − A . x ) + A . x ∗ ( B . y − A . y ) =(B.x-A.x)*C.y+(A.y-B.y)*C.x - A.y*(B.x-A.x)+A.x*(B.y-A.y) =(B.x−A.x)∗C.y+(A.y−B.y)∗C.x−A.y∗(B.x−A.x)+A.x∗(B.y−A.y)
注意到减号后面的部分只和 A 、 B A、B A、B有关,因此只需要把后面存下来,前面的作为比较函数即可。
struct Edge{
int u,v,w,t,c;
friend inline bool operator < (const Edge &a,const Edge &b)
{return a.c<b.c;}
}e[15010];
struct Point{
int x,y;
friend inline Point operator -(const Point &a,const Point &b)
{return (Point){a.x-b.x,a.y-b.y};
}
}ans,mn1,mn2;
iint getf(int x){return (x==fa[x])?(x):(fa[x]=getf(fa[x]));}
iint cross(Point x,Point y){return x.x*y.y-x.y*y.x;}
inline Point kruscal()
{
int tot=0;
Point now=(Point){0,0};
for(rint i=0;i<n;i++)fa[i]=i;
for(int i=1;i<=m;i++)
{
int U=getf(e[i].u),V=getf(e[i].v);
if(U!=V)
{
fa[U]=V;
tot++;
now.x+=e[i].w;
now.y+=e[i].t;
if(tot==n-1)
break;
}
}
ll Ans=(ll)ans.x*ans.y,Now=(ll)now.x*now.y;
if( Ans>Now || (Ans==Now&&now.x<ans.x) )
ans=now;
return now;
}
ivoid min_mul_tree(Point A,Point B)
{
for(int i=1;i<=m;i++)
e[i].c=e[i].t*(B.x-A.x)+e[i].w*(A.y-B.y);
sort(e+1,e+m+1);
Point C=kruscal();
if(cross(B-A,C-A)>=0)
return;
min_mul_tree(A,C);
min_mul_tree(C,B);
}
那么显然的,这个东西的运用范围也并不是特别广,貌似只在Time is Money见过.jpg
3、最小树形图
又出现了这么一类问题: