【python】Linear Algebra
代码来自
https://nbviewer.jupyter.org/github/ageron/handson-ml/blob/master/math_linear_algebra.ipynb?tdsourcetag=s_pctim_aiomsg
文章目录
- 1 Plotting Vectors
- 1.1 2D
- 1.2 3D
- 1.4 Euclidian Norm
- 1.5 Add
- 1.6 Geometric Translation
- 1.7 Multiplication by a Scalar
- 1.8 Normalized Vectors
- 1.9 Calculating the Angle between Vectors
- 1.10 Projecting a point onto an axis
- 2 Matrix
- 2.1 Diagonal matrix and Identity matrix
- 2.2 Matrix Multiplication
- 2.3 Matrix Transpose
- 2.3 Symmetric Matrix
- 3 Plotting a Matrix
- 3.1 Addition = multiple geometric translations
- 3.2 Scalar Multiplication
- 3.3 Matrix multiplication
- 3.3.1 Projection onto an axis
- 3.3.2 Rotation
- 3.3.3 Shear
- 3.3.4 Squeeze
- 3.3.5 Flip
- 3.4 Matrix Inverse
- 3.5 Determinant
- 3.6 Singular Value Decomposition(SVD)
- 3.7 Eigenvectors and Eigenvalues
- 3.8 Trace
1 Plotting Vectors
1.1 2D
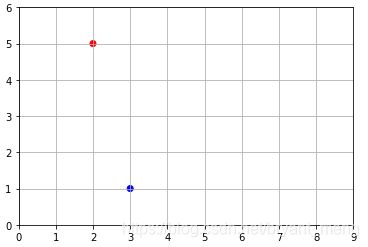
以 2D 为例,画点
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
u = np.array([2, 5])
v = np.array([3, 1])
x_coords, y_coords = zip(u, v)
plt.scatter(x_coords, y_coords, color=["r","b"])
plt.axis([0, 9, 0, 6])
plt.grid()
plt.show()
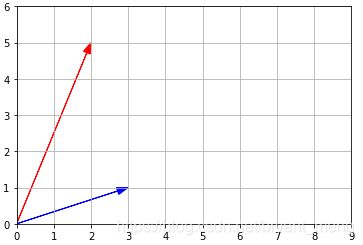
def plot_vector2d(vector2d, origin=[0, 0], **options):
return plt.arrow(origin[0], origin[1],
vector2d[0], vector2d[1],
head_width=0.2, head_length=0.3,
length_includes_head=True,**options)
plot_vector2d(u, color="r")
plot_vector2d(v, color="b")
plt.axis([0, 9, 0, 6])
plt.grid()
plt.show()
1.2 3D
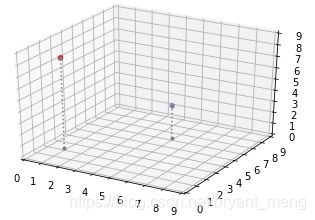
先画点
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
a = np.array([1, 2, 8])
b = np.array([5, 6, 3])
from mpl_toolkits.mplot3d import Axes3D
subplot3d = plt.subplot(111, projection='3d')
x_coords, y_coords, z_coords = zip(a,b)
subplot3d.scatter(x_coords, y_coords, z_coords,color=['r','b'])
# 设置坐标轴的范围
subplot3d.set_xlim3d([0, 9])
subplot3d.set_ylim3d([0, 9])
subplot3d.set_zlim3d([0, 9])
# 设置坐标轴的 label
subplot3d.set_xlabel("x")
subplot3d.set_ylabel("y")
subplot3d.set_zlabel("z")
plt.show()
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
a = np.array([1, 2, 8])
b = np.array([5, 6, 3])
from mpl_toolkits.mplot3d import Axes3D
def plot_vectors3d(ax, vectors3d, z0, **options):
for v in vectors3d:
x, y, z = v
ax.plot([x,x], [y,y], [z0, z], color="gray", linestyle='dotted', marker=".")
x_coords, y_coords, z_coords = zip(*vectors3d)
ax.scatter(x_coords, y_coords, z_coords, **options)
subplot3d = plt.subplot(111, projection='3d')
subplot3d.set_xlim3d([0, 9])
subplot3d.set_ylim3d([0, 9])
subplot3d.set_zlim3d([0, 9])
plot_vectors3d(subplot3d, [a,b], 0, color=("r","b"))
plt.show()
1.4 Euclidian Norm
也就向量的二范数,公式如下:
∣ ∣ u ⃗ ∣ ∣ 2 = ∑ i u ⃗ i 2 ||\vec{u}||_2 = \sqrt{\sum_i\vec{u}_i^2} ∣∣u∣∣2=i∑ui2
写个函数封装一下:
u = np.array([2, 5])
def vector_norm(vector):
squares = [element**2 for element in vector]
return sum(squares)**0.5
print("||", u, "|| = %s"% vector_norm(u))
output
|| [2 5] || = 5.385164807134504
其实呢,numpy 有现成的函数调用!
import numpy.linalg as LA
import numpy as np
u = np.array([2, 5])
LA.norm(u)
output
5.3851648071345037
验证一下计算的对不对(以二范数画圆)!
%matplotlib inline
import numpy.linalg as LA
import matplotlib.pyplot as plt
radius = LA.norm(u)
plt.gca().add_artist(plt.Circle((0,0), radius, color="#DDDDDD"))
plot_vector2d(u, color="red")
plt.axis([0, 8.7, 0, 6])
plt.grid()
plt.show()
def plot_vector2d 见前面 1.1 小节
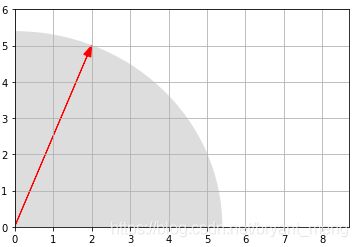
Looks about right!
1.5 Add
import numpy as np
u = np.array([2, 5])
v = np.array([3, 1])
print(" ", u)
print("+", v)
print("-"*10)
print(" ",u + v)
output
[2 5]
+ [3 1]
----------
[5 6]
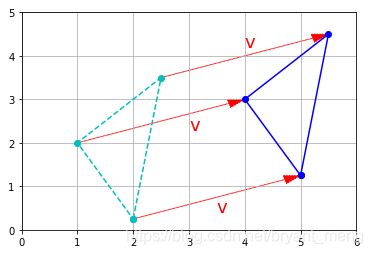
看看矢量加法对应的几何图像
%matplotlib inline
import matplotlib.pyplot as plt
plot_vector2d(u, color="r")
plot_vector2d(v, color="b")
plot_vector2d(v, origin=u, color="b", linestyle="dotted")
plot_vector2d(u, origin=v, color="r", linestyle="dotted")
plot_vector2d(u+v, color="g")
plt.axis([0, 9, 0, 7])
plt.text(0.7, 3, "u", color="r", fontsize=18)
plt.text(4, 3, "u", color="r", fontsize=18)
plt.text(1.8, 0.2, "v", color="b", fontsize=18)
plt.text(3.1, 5.6, "v", color="b", fontsize=18)
plt.text(2.4, 2.5, "u+v", color="g", fontsize=18)
plt.grid()
plt.show()
def plot_vector2d 见前面 1.1 小节

矢量的加法满足交换律(commutative)和结合律( associative).
- commutative: u ⃗ + v ⃗ = v ⃗ + u ⃗ \vec{u}+\vec{v} = \vec{v}+\vec{u} u+v=v+u
- associative: u ⃗ + ( v ⃗ + w ⃗ ) = ( u ⃗ + v ⃗ ) + w ⃗ \vec{u}+(\vec{v}+\vec{w}) = (\vec{u}+\vec{v})+\vec{w} u+(v+w)=(u+v)+w
1.6 Geometric Translation
每个点都加一个 vector,就可以实现 translation
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# 原来的三个点
t1 = np.array([2, 0.25])
t2 = np.array([2.5, 3.5])
t3 = np.array([1, 2])
x_coords, y_coords = zip(t1, t2, t3, t1)
plt.plot(x_coords, y_coords, "c--", x_coords, y_coords, "co") # 前面画线,后面画圆点
# 加了矢量
plot_vector2d(v, t1, color="r", linestyle=":")
plot_vector2d(v, t2, color="r", linestyle=":")
plot_vector2d(v, t3, color="r", linestyle=":")
# 加了矢量后的三个点
t1b = t1 + v
t2b = t2 + v
t3b = t3 + v
x_coords_b, y_coords_b = zip(t1b, t2b, t3b, t1b)
plt.plot(x_coords_b, y_coords_b, "b-",x_coords_b, y_coords_b, "bo")# 前面画线,后面画圆点
plt.text(4, 4.2, "v", color="r", fontsize=18)
plt.text(3, 2.3, "v", color="r", fontsize=18)
plt.text(3.5, 0.4, "v", color="r", fontsize=18)
plt.axis([0, 6, 0, 5])
plt.grid()
plt.show()
1.7 Multiplication by a Scalar
import numpy as np
u = np.array([2, 5])
print("1.5 *", u, "=", 1.5*u)
output
1.5 * [2 5] = [3. 7.5]
可视化一下
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
t1 = np.array([2, 0.25])
t2 = np.array([2.5, 3.5])
t3 = np.array([1, 2])
# 原来的三角
x_coords, y_coords = zip(t1, t2, t3, t1)
plt.plot(x_coords, y_coords, "c--", x_coords, y_coords, "co")
# 原来的vector
plot_vector2d(t1, color="r")
plot_vector2d(t2, color="r")
plot_vector2d(t3, color="r")
k = 2.5
t1c = k * t1
t2c = k * t2
t3c = k * t3
# scale后的三角
x_coords_c, y_coords_c = zip(t1c, t2c, t3c, t1c)
plt.plot(x_coords_c, y_coords_c, "b-", x_coords_c, y_coords_c, "bo")
# scale后的vector
plot_vector2d(k * t1, color="b", linestyle=":")
plot_vector2d(k * t2, color="b", linestyle=":")
plot_vector2d(k * t3, color="b", linestyle=":")
plt.axis([0, 9, 0, 9])
plt.grid()
plt.show()
- commutative(交换律): λ u ⃗ = u ⃗ λ \lambda \vec{u} = \vec{u} \lambda λu=uλ
- associative(结合律): λ 1 ( λ 2 u ⃗ ) = ( λ 1 λ 2 ) u ⃗ \lambda_1 (\lambda_2 \vec{u}) = (\lambda_1 \lambda_2) \vec{u} λ1(λ2u)=(λ1λ2)u
- distributive(分配率): λ ( u ⃗ + v ⃗ ) = λ u ⃗ + λ v ⃗ \lambda(\vec{u}+\vec{v}) = \lambda \vec{u}+\lambda \vec{v} λ(u+v)=λu+λv
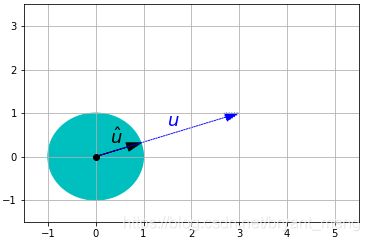
1.8 Normalized Vectors
u ⃗ ^ = u ⃗ ∣ ∣ u ⃗ ∣ ∣ \hat{\vec{u}} = \frac{\vec{u}}{||\vec{u}||} u^=∣∣u∣∣u
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import numpy.linalg as LA
v = np.array([3, 1])
plt.gca().add_artist(plt.Circle((0,0),1,color='c'))
plt.plot(0, 0, "ko")
plot_vector2d(v / LA.norm(v), color="k") # 向量除以模长
plot_vector2d(v, color="b", linestyle=":")
plt.text(0.3, 0.3, "$\hat{u}$", color="k", fontsize=18)
plt.text(1.5, 0.7, "$u$", color="b", fontsize=18)
plt.axis([-1.5, 5.5, -1.5, 3.5])
plt.grid()
plt.show()
1.9 Calculating the Angle between Vectors
c o s θ = u ⃗ ⋅ v ⃗ ∣ ∣ u ⃗ ∣ ∣ × ∣ ∣ v ⃗ ∣ ∣ cos\theta = \frac{\vec{u}\cdot\vec{v}}{||\vec{u}||\times||\vec{v}||} cosθ=∣∣u∣∣×∣∣v∣∣u⋅v
分子是 inner product
import numpy.linalg as LA
import numpy as np
u = np.array([2, 5])
v = np.array([3, 1])
def vector_angle(u, v):
cos_theta = u.dot(v) / LA.norm(u) / LA.norm(v)
return np.arccos(np.clip(cos_theta, -1, 1))
theta = vector_angle(u, v)
print("Angle =", theta, "radians")
print(" =", theta * 180 / np.pi, "degrees") # 弧度制和角度的转换
output
Angle = 0.868539395286 radians
= 49.7636416907 degrees
1.10 Projecting a point onto an axis
c o s θ = u ⃗ ⋅ v ⃗ ∣ ∣ u ⃗ ∣ ∣ × ∣ ∣ v ⃗ ∣ ∣ cos\theta = \frac{\vec{u}\cdot\vec{v}}{||\vec{u}||\times||\vec{v}||} cosθ=∣∣u∣∣×∣∣v∣∣u⋅v
p r o j u ⃗ v ⃗ = u ⃗ ⋅ v ⃗ ∣ ∣ u ⃗ ∣ ∣ u ⃗ ∣ ∣ u ⃗ ∣ ∣ proj_{\vec{u}}{\vec{v}} = \frac{\vec{u}\cdot\vec{v}}{||\vec{u}||} \frac{\vec{u}}{||\vec{u}||} projuv=∣∣u∣∣u⋅v∣∣u∣∣u
%matplotlib inline
import matplotlib.pyplot as plt
import numpy.linalg as LA
import numpy as np
u = np.array([2, 5])
v = np.array([3, 1])
u_normalized = u / LA.norm(u)
proj = u_normalized.dot(v) * u_normalized
# u v 矢量
plot_vector2d(u, color="r")
plot_vector2d(v, color="b")
#投影矢量
plot_vector2d(proj, color="g", linestyle="--")
plt.plot(proj[0], proj[1], "go")
# 垂线
plt.plot([proj[0], v[0]], [proj[1], v[1]], "b:")
# text
plt.text(1, 2, "$proj_u v$", color="k", fontsize=18)
plt.text(1.8, 0.2, "$v$", color="b", fontsize=18)
plt.text(0.8, 3, "$u$", color="r", fontsize=18)
plt.axis([0, 8, 0, 5.5])
plt.grid()
plt.show()
def plot_vector2d 见前面 1.1 小节
2 Matrix
2.1 Diagonal matrix and Identity matrix
- square matrix
- triangular matrix
- upper triangular matrix(上三角)
- lower triangular matrix(下三角)
- diagonal matrix(对角矩阵,
np.diag) - identity matrix(单位矩阵,
np.eye)
对角矩阵
import numpy as np
np.diag([4, 5, 6])
output
array([[4, 0, 0],
[0, 5, 0],
[0, 0, 6]])
import numpy as np
D = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
])
np.diag(D)
output
array([1, 5, 9])
单位矩阵
import numpy as np
np.eye(3)
output
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
2.2 Matrix Multiplication
矩阵乘用 A.dot(B)
import numpy as np
A = np.array([
[10,20,30],
[40,50,60]
])
D = np.array([
[ 2, 3, 5, 7],
[11, 13, 17, 19],
[23, 29, 31, 37]
])
E = A.dot(D)
E
output
array([[ 930, 1160, 1320, 1560],
[2010, 2510, 2910, 3450]])
2.3 Matrix Transpose
A.T ,注意 ( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT
import numpy as np
A = np.array([
[10,20,30],
[40,50,60]
])
D = np.array([
[ 2, 3, 5, 7],
[11, 13, 17, 19],
[23, 29, 31, 37]
])
print(A.dot(D).T == D.T.dot(A.T),'\n')
print(A.dot(D).T)
2.3 Symmetric Matrix
A T = A A^T = A AT=A
The product of a matrix by its transpose is always a symmetric matrix, for example:
import numpy as np
D = np.array([
[ 2, 3, 5, 7],
[11, 13, 17, 19],
[23, 29, 31, 37]
])
D.dot(D.T)
output
array([[ 87, 279, 547],
[ 279, 940, 1860],
[ 547, 1860, 3700]])
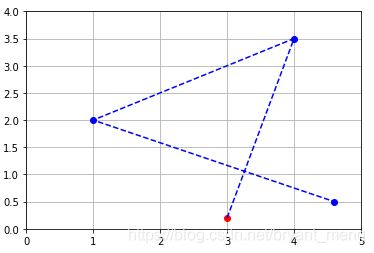
3 Plotting a Matrix
以 2 × 4 的矩阵为例,每一列是一个点
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
])
x_coords_P, y_coords_P = P
plt.scatter(x_coords_P, y_coords_P)
plt.axis([0, 5, 0, 4])
plt.show()

来看看点的顺序(Since the vectors are ordered, you can see the matrix as a path and represent it with connected dots.)
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
])
x_coords_P, y_coords_P = P
plt.plot(x_coords_P[0], y_coords_P[0], "ro") # 起点
plt.plot(x_coords_P[1:], y_coords_P[1:], "bo")
plt.plot(x_coords_P, y_coords_P, "b--") #线段
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
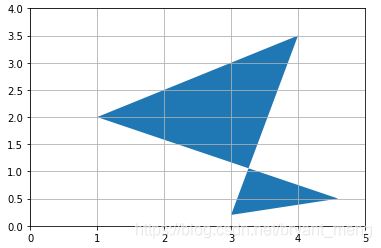
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Polygon
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
])
plt.gca().add_artist(Polygon(P.T)) # 注意这里的转置
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
如果不转置的话会报错 ValueError: 'vertices' must be a 2D list or array with shape Nx2.
下面来看看 geometric applications of matrix operations
3.1 Addition = multiple geometric translations
先看看矩阵加法的变化
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Polygon
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
])
H = np.array([
[ 0.5, -0.2, 0.2, -0.1],
[ 0.4, 0.4, 1.5, 0.6]
])
P_moved = P + H
# 画出变化前后的矩阵
plt.gca().add_artist(Polygon(P.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_moved.T, alpha=0.3, color="r"))
# 画每个点改变的箭头
for origin,vector in zip(P.T, H.T):
plot_vector2d(vector, origin=origin)
# 加上备注
plt.text(2.2, 1.8, "$P$", color="b", fontsize=18)
plt.text(2.0, 3.2, "$P+H$", color="r", fontsize=18)
plt.text(2.5, 0.5, "$H_{*,1}$", color="k", fontsize=18)
plt.text(4.1, 3.5, "$H_{*,2}$", color="k", fontsize=18)
plt.text(0.4, 2.6, "$H_{*,3}$", color="k", fontsize=18)
plt.text(4.4, 0.2, "$H_{*,4}$", color="k", fontsize=18)
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
def plot_vector2d 见前面 1.1 小节

如果每个点变换相同,那就是 simple geometric translation
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Polygon
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
])
H2 = np.array([
[-0.5, -0.5, -0.5, -0.5],
[ 0.4, 0.4, 0.4, 0.4]
])
P_translated = P + H2
# 画出变化前后的矩阵
plt.gca().add_artist(Polygon(P.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_translated.T, alpha=0.3, color="r"))
# 画每个点改变的箭头
for origin,vector in zip(P.T, H2.T):
plot_vector2d(vector, origin=origin)
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
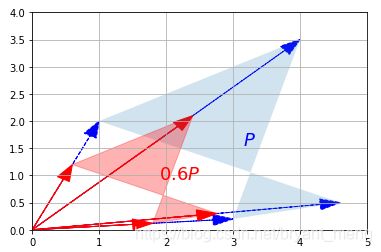
3.2 Scalar Multiplication
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Polygon
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
])
def plot_transformation(P_before, P_after, text_before, text_after, axis = [0, 5, 0, 4], arrows=False):
if arrows:
for vector_before, vector_after in zip(P_before.T, P_after.T):
plot_vector2d(vector_before, color="blue", linestyle="--") # 画出改变前的每个矢量
plot_vector2d(vector_after, color="red", linestyle="-") # 画出改变后的每个矢量
# 用 polygon 画改变前后的矩阵
plt.gca().add_artist(Polygon(P_before.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_after.T, alpha=0.3, color="r"))
# 写上 text
plt.text(P_before[0].mean(), P_before[1].mean(), text_before, fontsize=18, color="blue")
plt.text(P_after[0].mean(), P_after[1].mean(), text_after, fontsize=18, color="red")
plt.axis(axis)
plt.grid()
P_rescaled = 0.60 * P
plot_transformation(P, P_rescaled, "$P$", "$0.6 P$", arrows=True)
plt.show()
3.3 Matrix multiplication
3.3.1 Projection onto an axis
用 1*2 矩阵
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Polygon
U = np.array([[1, 0]]) # 1,2
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
def plot_projection(U, P):
U_P = U.dot(P)
# 投影轴
axis_end = 100 * U
plot_vector2d(axis_end[0], color="black")
# 画矩阵
plt.gca().add_artist(Polygon(P.T, alpha=0.2))
for vector, proj_coordinate in zip(P.T, U_P.T):
proj_point = proj_coordinate * U # 投影后的矢量 U.dot(P) * U
plt.plot(proj_point[0][0], proj_point[0][1], "ro") # 画点 [[]]
plt.plot([vector[0], proj_point[0][0]], [vector[1], proj_point[0][1]], "r--") # 画 [x0,x1],[y0,y1]
#也即原来的向量往投影后的向量画线,也就是垂线
plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()
plot_projection(U, P)
def plot_vector2d 见前面 1.1 小节
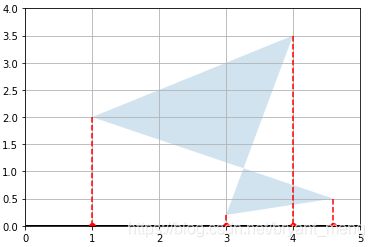
此时投影轴为x
改变 U = np.array([[1, 0]]) 为 U = np.array([[0, 1]]),投影轴为 y
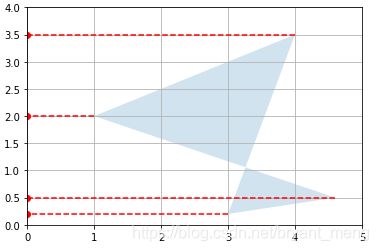
设置投影轴为倾斜的 c o s 3 0 ∘ cos30^{\circ} cos30∘
angle30 = 30 * np.pi / 180 # angle in radians
U_30 = np.array([[np.cos(angle30), np.sin(angle30)]])
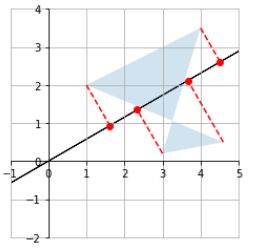
plot_projection(U_30, P)
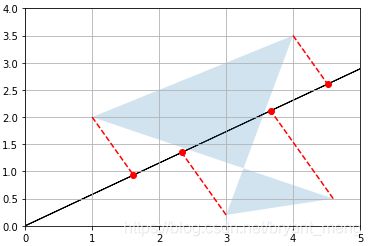
这里要仔细分析一下,为什么是往 y = t a n θ ⋅ x y = tan \theta \cdot x y=tanθ⋅x 直线上投影(这里 θ = 30 ° \theta = 30° θ=30°)
我们回顾下投影的表达式
c o s θ = u ⃗ ⋅ v ⃗ ∣ ∣ u ⃗ ∣ ∣ × ∣ ∣ v ⃗ ∣ ∣ cos\theta = \frac{\vec{u}\cdot\vec{v}}{||\vec{u}||\times||\vec{v}||} cosθ=∣∣u∣∣×∣∣v∣∣u⋅v
p r o j u ⃗ v ⃗ = u ⃗ ⋅ v ⃗ ∣ ∣ u ⃗ ∣ ∣ u ⃗ ∣ ∣ u ⃗ ∣ ∣ proj_{\vec{u}}{\vec{v}} = \frac{\vec{u}\cdot\vec{v}}{||\vec{u}||}\frac{\vec{u}}{||\vec{u}||} projuv=∣∣u∣∣u⋅v∣∣u∣∣u
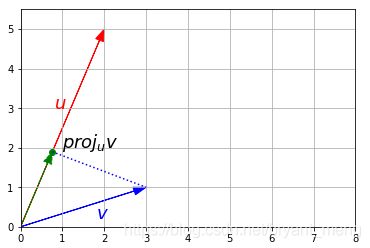
当 u ⃗ \vec{u} u 是单位向量的时候, ∣ ∣ u ⃗ ∣ ∣ ||\vec{u}|| ∣∣u∣∣ 为1,所以公式可以进一步化简为
p r o j u ⃗ v ⃗ = u ⃗ ⋅ v ⃗ u ⃗ proj_{\vec{u}}{\vec{v}} = \vec{u}\cdot \vec{v} \vec{u} projuv=u⋅vu
总结:向量 v ⃗ \vec{v} v 往单位向量 u ⃗ \vec{u} u 上投影的模长就等于该向量与单位向量的内积(inner product),投影的方向同单位向量的方向!
所以,我们用矩阵 U_30 = np.array([[np.cos(angle30), np.sin(angle30)]]) 乘以原来的矩阵,对应到矩阵的每一列,也就是每一个坐标的话,相当于每个列向量往 U_30 上投影


这样对比着看就显而易见了,嘿嘿嘿!(上面右图是在 def plot_projection 函数中添加如下代码的结果)
def plot_projection(U, P):
#………
# 画向量
for i in range(np.shape(P)[1]):#遍历所
plot_vector2d(P[:,i],color="r")
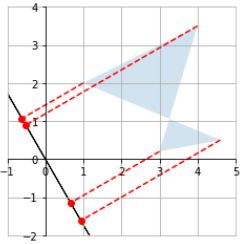
3.3.2 Rotation
现在探究下用 2*2 矩阵,2*2 乘以原来的 2*4,结果还是 2*4
修改下 def plot_projection(U, P): 函数
- 把坐标轴的尺度统一(正方形,而不是长方形)
- 画个坐标轴
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Polygon
def plot_projection(U, P):
U_P = U.dot(P)
# 投影轴
axis_end = 100 * U
plot_vector2d(axis_end[0], color="black")
plot_vector2d(-axis_end[0], color="black")
# 画矩阵
plt.gca().add_artist(Polygon(P.T, alpha=0.2))
for vector, proj_coordinate in zip(P.T, U_P.T):
proj_point = proj_coordinate * U # 投影后的矢量 U.dot(P) * U
plt.plot(proj_point[0][0], proj_point[0][1], "ro") # 画点 [[]]
plt.plot([vector[0], proj_point[0][0]], [vector[1], proj_point[0][1]], "r--") # 画 [x0,x1],[y0,y1]
plt.axis([-1, 5, -2, 4])
# 画 x 轴和 y 轴
ax = plt.gca() # x,y
# spines = 上下左右四条黑线
ax.spines['right'].set_color('none') # 让右边的黑线消失
ax.spines['top'].set_color('none') # 让上边的黑线消失
ax.xaxis.set_ticks_position('bottom') # 把下面的黑线设置为x轴
ax.yaxis.set_ticks_position('left') # 把左边的黑线设置为y轴
ax.spines['bottom'].set_position(('data',0)) # 移动x轴到指定位置,本例子为0
ax.spines['left'].set_position(('data',0)) # 移动y轴到指定位置,本例子为0
# 设置 x 轴和 y 轴等距
plt.gca().set_aspect('equal', adjustable='box')
plt.grid()
plt.show()
我们用以下矩阵来乘以原来的 P P P 矩阵!
V = [ c o s 3 0 ∘ s i n 3 0 ∘ c o s 12 0 ∘ s i n 12 0 ∘ ] V = \begin{bmatrix} cos30^{\circ} & sin30^{\circ}\\ cos120^{\circ} & sin120^{\circ} \end{bmatrix} V=[cos30∘cos120∘sin30∘sin120∘]
也即
V ⋅ P = [ c o s 3 0 ∘ s i n 3 0 ∘ c o s 12 0 ∘ s i n 12 0 ∘ ] ⋅ [ 3.0 4.0 1.0 4.6 0.2 3.5 2.0 0.5 ] = [ 2.69807621 5.21410162 1.8660254 4.23371686 − 1.32679492 1.03108891 1.23205081 − 1.8669873 ] V \cdot P = \begin{bmatrix} cos30^{\circ} & sin30^{\circ}\\ cos120^{\circ} & sin120^{\circ} \end{bmatrix}\cdot \begin{bmatrix} 3.0 & 4.0 & 1.0 & 4.6\\ 0.2 & 3.5 & 2.0 & 0.5 \end{bmatrix} = \begin{bmatrix} 2.69807621 & 5.21410162 & 1.8660254 & 4.23371686 \\ -1.32679492 & 1.03108891 & 1.23205081 & -1.8669873 \end{bmatrix} V⋅P=[cos30∘cos120∘sin30∘sin120∘]⋅[3.00.24.03.51.02.04.60.5]=[2.69807621−1.326794925.214101621.031088911.86602541.232050814.23371686−1.8669873]
有了前面投影的基础,我们可以理解为,新的横坐标的绝对值是原来的点往 θ = 3 0 ∘ \theta = 30^{\circ} θ=30∘ 的直线上投影的模长,新的纵坐标的绝对值是原来的点往 θ = 12 0 ∘ \theta=120^{\circ} θ=120∘ 的直线上投影的模长!
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
angle30 = 30 * np.pi / 180 # angle in radians
U_30 = np.array([[np.cos(angle30), np.sin(angle30)]])
plot_projection(U_30, P)
angle120 = 120 * np.pi / 180 # angle in radians
U_120 = np.array([[np.cos(angle120), np.sin(angle120)]])
plot_projection(U_120, P)
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Polygon
import numpy.linalg as LA
def cal_theta(P,P_rotated):
theta = [] # 存放每个坐标的角度变换
for i in range(P_rotated.shape[1]):#遍历每一列
radian = P[:,i].dot(P_rotated[:,i]) / (LA.norm(P[:,i])*LA.norm(P_rotated[:,i])) # 计算弧度
theta.append(radian*180/np.pi) #转化为角度
return theta
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
angle30 = 30 * np.pi / 180 # angle in radians
angle120 = 120 * np.pi / 180 # angle in radians
V = np.array([
[np.cos(angle30), np.sin(angle30)],
[np.cos(angle120), np.sin(angle120)]
])
P_rotated = V.dot(P)
theta = cal_theta(P,P_rotated)
print(theta)
plot_transformation(P, P_rotated, "$P$", "$VP$", [-1, 7, -1, 5], arrows=True)
plt.show()
其中 def plot_transformation 见 3.2 小节 Scalar Multiplication
output
[49.61960058796129, 49.61960058796129, 49.61960058796129, 49.61960058796128]

哈哈哈,大吃一惊,怎么是顺时针移动了 4 9 ∘ + 49^{\circ}+ 49∘+,把投影换成负数试试
angle30 = 30 * np.pi / 180 # angle in radians
angle120 = 120 * np.pi / 180 # angle in radians
改为
angle30 = -30 * np.pi / 180 # angle in radians
angle120 = 60 * np.pi / 180 # angle in radians
output
[49.61960058796129, 49.61960058796129, 49.61960058796129, 49.61960058796128]

逆时针转动了 4 9 ∘ + 49^{\circ}+ 49∘+
之前我们保持了横纵坐标的变化的差值为 9 0 ∘ 90^{\circ} 90∘,这样形状就不会变化!下面试试别的
3.3.3 Shear
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
F_shear = np.array([
[1, 1.5],
[0, 1]
])
plot_transformation(P, F_shear.dot(P), "$P$", "$F_{shear} P$",
axis=[0, 10, 0, 7])
plt.show()
其中 def plot_transformation 见 3.2 小节 Scalar Multiplication

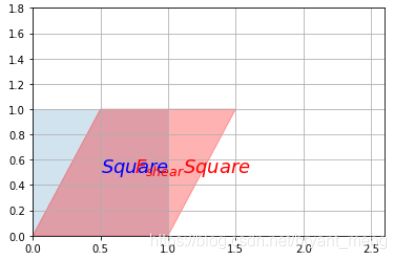
看看作用在方阵上的效果
F_shear = np.array([
[1, 1.5],
[0, 1]
])
Square = np.array([
[0, 0, 1, 1],
[0, 1, 1, 0]
])
plot_transformation(Square, F_shear.dot(Square), "$Square$", "$F_{shear} Square$",
axis=[0, 2.6, 0, 1.8])
plt.show()
1)偏离 0.5 和 1.0
F_shear = np.array([
[1, 0.5],
[0, 1]
])
F_shear = np.array([
[1, 1.0],
[0, 1]
])
F_shear = np.array([
[1, 1.5],
[0, 1]
])
F_shear = np.array([
[1, -0.5],
[0, 1]
])
F_shear = np.array([
[1, 0],
[0.5, 1]
])
F_shear = np.array([
[1, 0.5],
[0.5, 1]
])
3.3.4 Squeeze
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
F_squeeze = np.array([
[1.2, 0],
[0, 1/1.2]
])
plot_transformation(P, F_squeeze.dot(P), "$P$", "$F_{squeeze} P$",
axis=[0, 7, 0, 5])
plt.show()
其中 def plot_transformation 见 3.2 小节 Scalar Multiplication
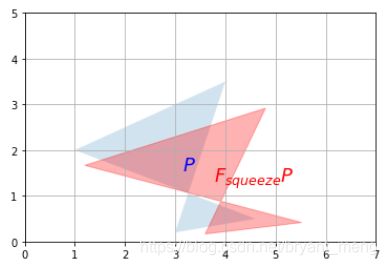
F_squeeze = np.array([
[1.5, 0],
[0, 1/1.5]
])
F_squeeze = np.array([
[1.5, 0],
[0, 1.5]
])
3.3.5 Flip
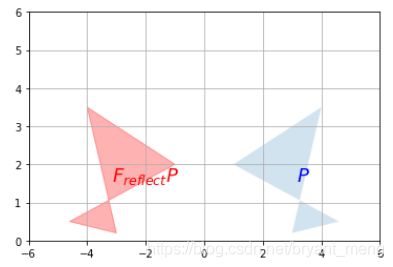
1)Vertical flip
F_reflect = np.array([
[1, 0],
[0, -1]
])
plot_transformation(P, F_reflect.dot(P), "$P$", "$F_{reflect} P$",
axis=[-2, 9, -4.5, 4.5])
plt.show()
其中 def plot_transformation 见 3.2 小节 Scalar Multiplication
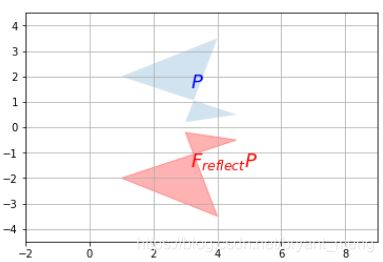
2)Horizental flip
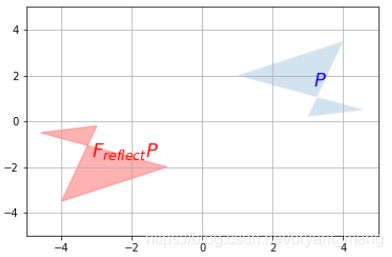
F_reflect = np.array([
[-1, 0],
[0, 1]
])
plot_transformation(P, F_reflect.dot(P), "$P$", "$F_{reflect} P$",
axis=[-6, 6, 0, 6])
plt.show()
F_reflect = np.array([
[-1, 0],
[0, -1]
])
plot_transformation(P, F_reflect.dot(P), "$P$", "$F_{reflect} P$",
axis=[-5, 5, -3.5, 3.5])
plt.show()
3.4 Matrix Inverse
逆矩阵的求法如下
import numpy as np
import numpy.linalg as LA
F_shear = np.array([
[1, 1.5],
[0, 1]
])
F_inv_shear = LA.inv(F_shear)
F_inv_shear
output
array([[ 1. , -1.5],
[ 0. , 1. ]])
接下来探讨下逆矩阵的魅力
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
F_shear = np.array([
[1, 1.5],
[0, 1]
])
F_inv_shear = np.array([
[1, -1.5],
[0, 1]
])
print(F_shear.dot(F_inv_shear),'\n')
print(F_inv_shear.dot(F_shear))
# 原矩阵和逆矩阵相乘为I
P_sheared = F_shear.dot(P)
P_unsheared = F_inv_shear.dot(P_sheared)
plot_transformation(P_sheared, P_unsheared, "$P_{sheared}$", "$P_{unsheared}$",
axis=[0, 10, 0, 7])
plt.plot(P[0], P[1], "b--") # set[x],set[y],画虚线
plt.show()
其中 def plot_transformation 见 3.2 小节 Scalar Multiplication
output
[[1. 0.]
[0. 1.]]
[[1. 0.]
[0. 1.]]
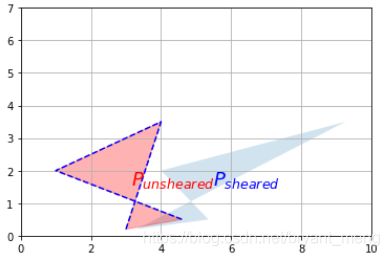
蓝色虚线表示原来的矩阵,可以看到,左乘 shear 之后,然后再左乘 shear 的逆,图形没有任何变化,这是因为
F − 1 F = I , F F − 1 = I F^{-1}F = I,FF^{-1} = I F−1F=I,FF−1=I
然后单位矩阵乘以任何矩阵结果都是任何矩阵本身!
3.5 Determinant
import numpy as np
import numpy.linalg as LA
M = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 0]
])
LA.det(M)
output
27.0
P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
F_scale = np.array([
[0.5, 0],
[0, 0.5]
])
plot_transformation(P, F_scale.dot(P), "$P$", "$F_{scale} \cdot P$",
axis=[0, 6, -1, 4])
plt.show()
其中 def plot_transformation 见 3.2 小节 Scalar Multiplication

P = np.array([
[3.0, 4.0, 1.0, 4.6],
[0.2, 3.5, 2.0, 0.5]
]) # 2,4
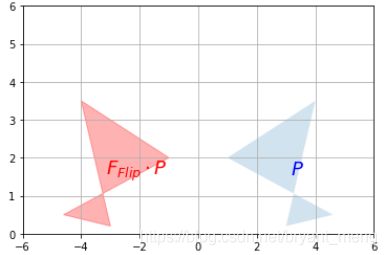
F_flip = np.array([
[-1, 0],
[0, 1]
])
plot_transformation(P, F_flip.dot(P), "$P$", "$F_{Flip} \cdot P$",
axis=[-6, 6, 0, 6])
plt.show()
LA.det(F_flip)
结果是 -1.0
对角矩阵的特征值等于对角线上的元素,而行列式的值等于特征值的乘积!
3.6 Singular Value Decomposition(SVD)
关于 SVD 的数学推导可以参考 Singular Value Decomposition
A = U Σ V T A = U \Sigma V^T A=UΣVT
import numpy as np
import numpy.linalg as LA
F_shear = np.array([
[1, 1.5],
[0, 1]
])
# 对 F_shear 矩阵进行 SVD
U, S_diag, V_T = LA.svd(F_shear)
print(U,'\n')
print(S_diag,'\n')
print(V_T,'\n')
# 返回的是主对角线的元素,我们把它变成对角矩阵
S = np.diag(S_diag)
print(S)
output
[[ 0.89442719 -0.4472136 ]
[ 0.4472136 0.89442719]]
[2. 0.5]
[[ 0.4472136 0.89442719]
[-0.89442719 0.4472136 ]]
[[2. 0. ]
[0. 0.5]]
我们还原回去试试
U.dot(np.diag(S_diag)).dot(V_T)
output
array([[1. , 1.5],
[0. , 1. ]])
nice,和 F_shear 矩阵一样,F_shear 作用在方阵的效果如下:
Square = np.array([
[0, 0, 1, 1],
[0, 1, 1, 0]
])
plot_transformation(Square, F_shear.dot(Square), "$Square$", "$F_{shear} Square$",
axis=[-0.5, 3.5 , -1.5, 1.5])
plt.show()
其中 def plot_transformation 见 3.2 小节 Scalar Multiplication
接下来我们看看 SVD 分解后每一个部分的作用!
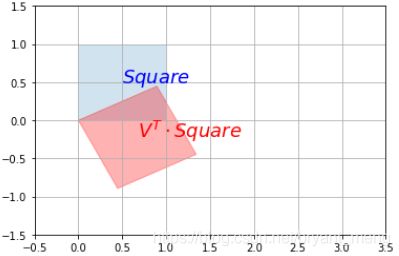
1)首先是 V T V^T VT
plot_transformation(Square, V_T.dot(Square), "$Square$", "$V^T \cdot Square$",
axis=[-0.5, 3.5 , -1.5, 1.5])
plt.show()
2)再是 S S S
plot_transformation(V_T.dot(Square), S.dot(V_T).dot(Square), "$V^T \cdot Square$", "$\Sigma \cdot V^T \cdot Square$",
axis=[-0.5, 3.5 , -1.5, 1.5])
plt.show()
3)最后是 U U U
plot_transformation(S.dot(V_T).dot(Square), U.dot(S).dot(V_T).dot(Square),"$\Sigma \cdot V^T \cdot Square$", "$U \cdot \Sigma \cdot V^T \cdot Square$",
axis=[-0.5, 3.5 , -1.5, 1.5])
plt.show()
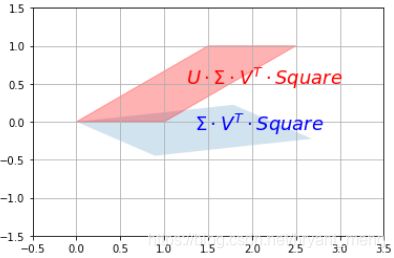
And we can see that the result is indeed a shear mapping of the original unit square.
3.7 Eigenvectors and Eigenvalues
import numpy as np
import numpy.linalg as LA
A = np.array([
[1, 1, 0],
[1, 2, 1],
[0, 1, 1],
])
eigenvalues, eigenvectors = LA.eig(A)
print(eigenvalues,'\n')
print(eigenvectors)
output
[ 3.00000000e+00 1.00000000e+00 -3.36770206e-17]
[[-4.08248290e-01 7.07106781e-01 5.77350269e-01]
[-8.16496581e-01 2.61239546e-16 -5.77350269e-01]
[-4.08248290e-01 -7.07106781e-01 5.77350269e-01]]
可以对比下 Singular Value Decomposition 的一个例子的结果
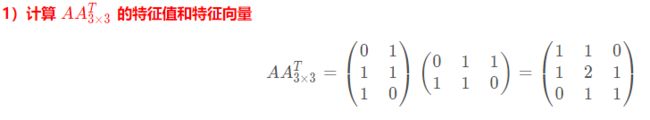
特征值为 3,1,0,对应的特征向量如下
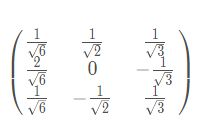
试试
from math import sqrt
print(1/sqrt(6))
print(1/sqrt(2))
print(1/sqrt(3))
output
0.4082482904638631
0.7071067811865475
0.5773502691896258
没有问题,哈哈,不过好像不能表示 0
3.8 Trace
等于对角线上元素的和
import numpy as np
import numpy.linalg as LA
D = np.array([
[100, 200, 300],
[ 10, 20, 30],
[ 1, 2, 3],
])
np.trace(D)