二分图的最大匹配问题和基数顶点覆盖问题(1)
首先,这个知识点补充的原因是我在阅读文章《Approximation Algorithms》时所遇 到的新问题。在文章的1.2可以看到这么一句话:
Consider decision versions of the cardinality vertex cover and maximum
matching problems.
翻译过来就是:考虑基数顶点覆盖的决策版本和最大匹配问题。
这时就必须掌握基数顶点覆盖和最大匹配问题。而下文中的两个子问题则具体描述了最小顶点覆盖问题与最大匹配问题的一个大小的比较。
• Is the size of the minimum vertex cover in G at most k?
• Is the size of the maximum matching in G at least l?
首先我们先来解释一下二分图、最大匹配、最小顶点覆盖的基本概念。
抛开书中给的刻板定理,简单的可以理解为:
二分图:把一个图的顶点可以划分为两个不相交的集合,使得每一条边都链接着集合中的顶点。如果存在这样的图,那么就可以称为二分图。换而言之,不含有“奇数条边的环”的图。
最大匹配:一个图中所有的匹配中所含边数最多的匹配,那么就可以称之为这个图的最大匹配
在这篇《Approximation Algorithms》中的解释为:A matching of maximum cardinality in H is called a maximum matching, and a matching that is maximal under inclusion is called a maximal matching. A maximal matching can clearly be computed in polynomial time by simply greedily picking edges and removing endpoints of picked edges.
而匹配的概念则为:Given a graph H = (U, F), a subset of the edges M ⊆ F is said to be a matching if no two edges of M share an endpoint.简单的说,就是一个匹配是一个边的集合,其中任意的两条边都没有公共的顶点。
基数顶点覆盖:Given an undirected graph G = (V,E), and a cost function on vertices c : V → Q+, fifind a minimum cost vertex cover,i.e., a set V ⊆ V such that every edge has at least one endpoint incident at V . The special case, in which all vertices are of unit cost, will be called the cardinality vertex cover problem.简单的说,就是选定一个点就相当于覆盖了以它为顶点的所有的边。而最小顶点覆盖则是,这中间可以覆盖所有边的点使用数量为最少的。
接下来,我们将重点讲解最大匹配问题。而最小顶点覆盖与他们之间的关系将在后续的文章中出现。
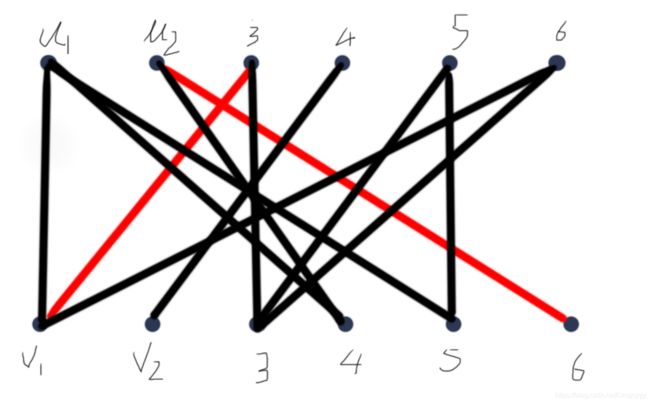
首先我们给出一个二分图,如下图所示:
已知题目给出两条匹配路径M1={(u2,v1),(u2,v6)},图的上边所没有匹配到的点为S1={u1,u4,u5,u6}。这时我们可以自行选择一个为匹配的顶点,如u1。可以看出当我们选择u1时,可以得到的路径为:(u1,v1),(u1,v4),(u1,v5)。这时由于已经有给出的匹配(v1,u3)所以我们此时选择(u1,v1)。我们需要一条增广路来进行匹配。
增广路:从一个未匹配的点出发,走交替路,如果途径另一个为匹配的点则这条交替路为增广路。
增广路P1={(u1,v1)(v1,u3)(u3,v3)}其中u3属于M1。所以此时对M1与P1做一个异或运算,可以得出:
M2={(u1,v1)(u2,v6)(u3,v3)}
增广路P2={(u4,v2)},P2与M2做一个异或运算可得:
M3={(u1,v1)(u2,v6)(u3,v3)(u4,v2)}
增广路P3={(u5,v3)(v3,u3)(u3,v1)(v1,u1)(u1,v4)}
M4={(u5,v3)(u3,v1)(u1,v4)(u2,v6)(u4,v2)}
增广路P4={(u6,v1)(v1,u3)(u3,v3)(v3,u5)(u5,v5)}
M5={(u6,v3),(u3,v3)(u5,v5)(u1,v4)(u2,v6)(u4,v2)}
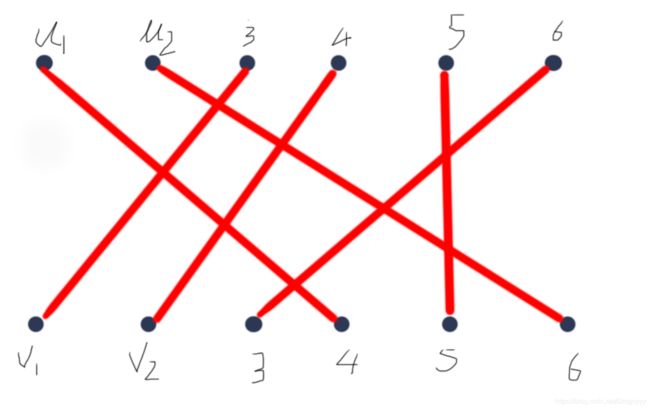
第二种情况:P'={(u6,v3)(u3,v5)(u5,v5)}
M'={(u1,v4)(u2,v6)(u3,v1)(u3,v2)(u5,v5)(u6,v3)}
如图所示为最大匹配,同时也为完美匹配(所有匹配的边链接所有的顶点)