Multi-Hop Paragraph Retrieval for Open-Domain Question Answering
ACL 2019 Multi-Hop Paragraph Retrieval for Open-Domain Question Answering
github
Question Answering问题粗略的可以分为两类:
- Reading Comprehension,RC:模型需要根据给定的问题和对应的输入文档找出答案所在,而且根据问题所对应文档的数目可分为single-hop reasoning和multi-hop reasoning。前一种任务相对来说较为简单,后一种可能需要进行迭代式推断
- open-domain QA:对于问题来说并没有对应的文档,模型需要首先从大型知识库(knowledge base)中进行检索寻找可能包含答案的文档,然后使用RC的方法进行答案的推断
本文所关注的问题便是multi-hop open-domain QA 问题,它需要模型同时进行有效的检索和文本理解,因此解决起来更为困难。作者为此提出了一种嵌套于大型知识库中的多支持文档检索的方法,它通过使用句子级的表示和拼接问题向量和文档向量的方式进行迭代式检索。最后在SQuAD-Open和HotpotQA两个数据集上进行实现取得了SOTA。
open-domain QA问题可以形式化定义为 ( K S , Q , A ) (KS, Q, A) (KS,Q,A),其中 K S KS KS表示需要检索的知识库,它通常由很多个文档组 P i P_{i} Pi组成; Q Q Q表示给定的问题; A A A表示对应的答案所在,它通常以span的形式表示,具体为对应的token的索引序列 p j 1 , . . . , p j n p_{j1},...,p_{jn} pj1,...,pjn。因此,总体来说open-domain QA问题就是为了寻找一个函数 ϕ \phi ϕ使其满足 A = ϕ ( Q , K S ) A = \phi(Q, KS) A=ϕ(Q,KS)。
总体来说,open-domain QA首先需要从大型知识库中检索到相应于问题的文档,然后再从文档中推断答案,而且在推断时需要从前一篇中推断出所需的内容后才能从后面的文档中推断另外的答案。
Model
本文所提出的模型称为 MUPPET \text{MUPPET} MUPPET,它的模型架构如下所示:
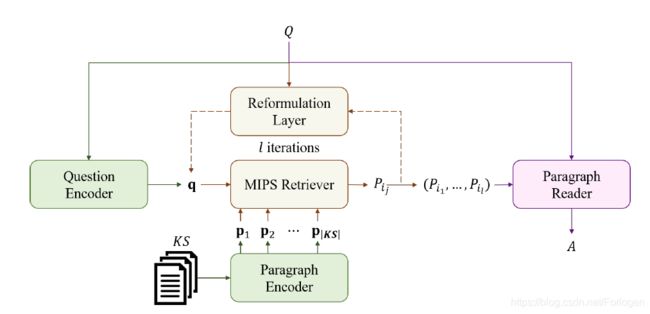
从上图可以看出, MUPPET \text{MUPPET} MUPPET主要分为如下的三个部分:
- Paragraph Encoder and Question Encoder:它们负责将问题和文档编码为对应的 d d d维表示向量
- MIPS Retriever: 使用MIPS迭代的从文档集中找出对应与问题的具体文档
- Paragraph Reader:具体完成从检索得到的文档中推断答案
所谓的迭代式检索也很好理解,当给定问题和文档集后,首先将问题转换为对应的搜索向量 q q q,然后使用MIPS从知识库中第一次检索得到 K K K个相关的文档 { P 1 Q , . . . , P k Q } \{P_{1}^Q, ..., P_{k}^Q\} {P1Q,...,PkQ},接着再将其转换为新的向量,这次再从中选择 k k k个向量 { q ~ 1 s , . . . , q ~ k s } \{\tilde{q}_{1}^s,...,\tilde{q}_{k}^s\} {q~1s,...,q~ks},同样的再进行搜索对应的文档。
Paragraph Encoder and Question Encoder
假设文档 P P P包含 k k k个句子 ( s 1 , . . , s k ) (s_{1},..,s_{k}) (s1,..,sk),其中每个句子 s i s_{i} si包含m个词 ( t 1 , . . , t m ) (t_{1},..,t_{m}) (t1,..,tm),那么使用Encoder将其编码为 k k k个 d d d维的表示向量;问题 Q Q Q同样可以表示对应的表示向量。
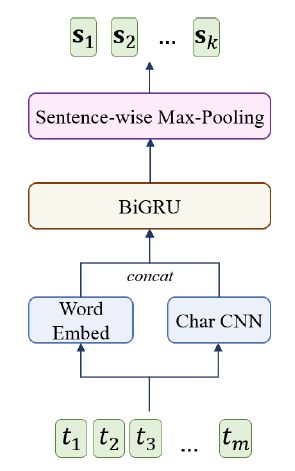
模型编码的方式也很常见,就是将token进行word-level和character-level两个层次的编码,然后将表示向量进行拼接后通过BiGRU和Max-Pooling后得到对应的表示向量 s i s_{i} si。
为了后续的答案的推断,这里通过Reformulation Component将问题的表示向量 Q Q Q和文档的表示向量 P P P通过Bi-Attention层得到一个新的向量 q ~ \tilde{q} q~。
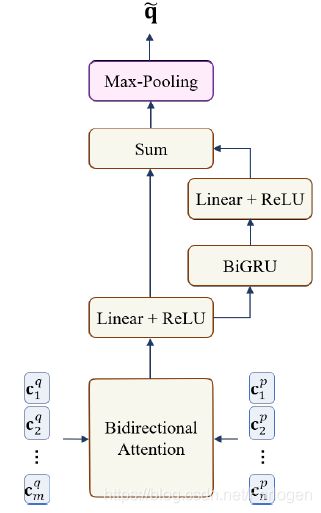
其中问题中的第 i i i个词和文档中第 j j j个词计算注意力分数 a i j = w 1 a ⋅ c i q + w 2 a ⋅ c j p + w 3 a ⋅ ( c i q ⨀ c j p ) a_{ij}=w_{1}^a \cdot c_{i}^q + w_{2}^a \cdot c_{j}^p +w_{3}^a \cdot(c_{i}^q \bigodot c_{j}^p) aij=w1a⋅ciq+w2a⋅cjp+w3a⋅(ciq⨀cjp),然后对于问题中的每个词计算向量 a i = ∑ j = 1 n p α i j c j p a_{i} = \sum_{j=1}^{n_{p}}\alpha_{ij} c_{j}^p ai=∑j=1npαijcjp;同样的也可以得到文档相对于问题的向量 a p a^p ap。接着将上述得到的向量进行拼接后通过Linear layer、BiGRU layer和Max-Pooling layer得到最终的表示 q ~ \tilde{q} q~。
通过上述的工作模型就得到关于问题和文档的表示向量,接着就需要计算相关性分数筛选出和问题相关的文档。
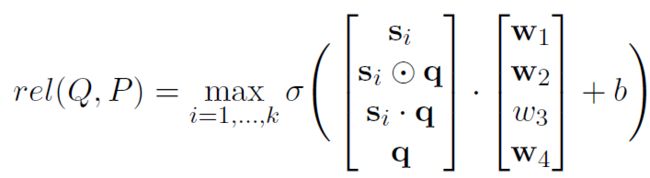
每个样本都可以表示为 ( Q , P 1 , P 2 ) (Q,P^1,P^2) (Q,P1,P2),其中 Q Q Q表示问题向量, P 1 P^1 P1表示第一次检索得到的文档向量, P 2 P^2 P2表示第二次检索得到的文档向量。 P 1 P^1 P1当包含相对于问题的事实后才认为是相关的,而 P 2 P^2 P2只有和 P 1 P^1 P1两者一起组成相对于问题的事实才认为是相关的。在得到了上述形式的样本后,训练函数包含交叉熵(cross entropy)和排序损失(ranking loss)两部分 : L C E = − 1 N ∑ i = 1 N y i log ( r e l ( Q i , P i ) ) + ( 1 − y i ) log ( 1 − r e l ( Q i , P i ) ) L R = 1 M ∑ i = 1 M max ( 0 , γ − q i p o s + q i n e g ) L_{CE}=- \frac{1}{N} \sum_{i=1}^N y_{i} \log (rel(Q_{i}, P_{i})) + (1-y_{i}) \log (1-rel(Q_{i}, P_{i})) \\ L_{R} = \frac{1}{M} \sum_{i=1}^M \max(0, \gamma-q_{i}^{pos} + q_{i}^{neg}) LCE=−N1i=1∑Nyilog(rel(Qi,Pi))+(1−yi)log(1−rel(Qi,Pi))LR=M1i=1∑Mmax(0,γ−qipos+qineg)
最终的损失函数为两者的线性插值形式 L = L C E + γ L R L=L_{CE} + \gamma L_{R} L=LCE+γLR。
Paragraph Reader
这里使用S-norm进行答案的推断,即进行起始和终止索引的推断。Reader训练对应的损失函数为 L s t a r t = − log ( ∑ j ∈ P Q ∑ k ∈ A j e s k j ∑ j ∈ P Q ∑ i = 1 n j e e i j ) L_{start}= - \log (\frac{\sum_{j \in P^Q} \sum_{k \in A_{j}}e^{s_{kj}}}{\sum_{j \in P^Q} \sum_{i=1}^{n_{j}} e^{e_{ij}}}) Lstart=−log(∑j∈PQ∑i=1njeeij∑j∈PQ∑k∈Ajeskj)
最终的损失函数为 L s p a n = L s t a r t + L e n d L_{span} = L_{start} + L_{end} Lspan=Lstart+Lend。
实验部分可见原文~