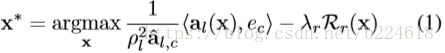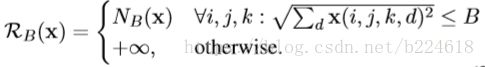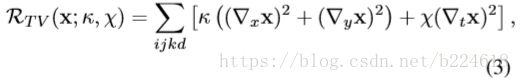读书笔记31：What have we learned from deep representations for action recognition?（CVPR2018）

http://openaccess.thecvf.com/content_cvpr_2018/papers/Feichtenhofer_What_Have_We_CVPR_2018_paper.pdf

摘要：首先是背景，深度模型在计算机视觉的每个领域都有部署，因此，理解这些深度模型得到的representation到底是怎么工作的，以及这些representation到底抓去了什么信息就变得越来越重要。接着说本文的工作，本文通过可视化two-stream模型在进行动作识别任务的时候学到了什么来探索这个问题。得到的观察结果主要有以下几点，首先，cross-stream fusion使得学习的过程能够真正的学习到spatiotemporal feature，而不是仅仅分开两支，一支只获得appearance feature，一支只获得motion feature；第二点是网络得到的local representation可以非常专一，非常针对性的表示某一class的特征（class specific），也可能会更加一般一些，能够包含多个类的特征，我觉得这个意思就是，有一些local representation可以直接指明这个特征是属于某一个class的，有些可能就是缩小了范围，指明这个特征可能对应着某几个class；第三点观察结果是，通过网络结构的层级结构，feature变得越来越抽象，并且展示出越来越高的稳定性，对于数据中一些无关紧要的变化（例如不同速度的motion pattern）有着越来越高的invariance；第四点是这种可视化手段不仅能对学到的representation使用，还能对training data使用，揭示出数据的独特性，可以用来解释为什么有些时候模型不能正确的进行预测。

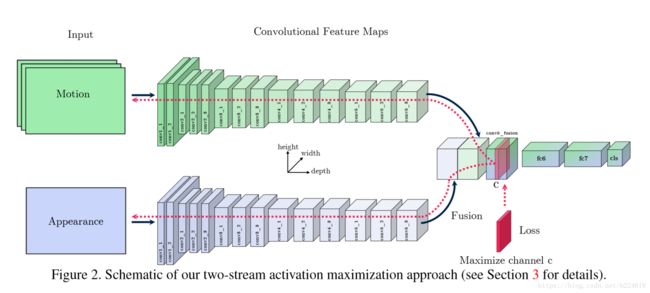
本文采取的是activation maximization的方式进行可视化，这个activation指的是某一个hidden layer的激活值，目的在于寻找恰当的输入，可以使得某一个感兴趣的激活值最大化。本文采取的方式示意图如下

这是一个two-flow的CNN网络，一个输入的是motion信息（例如optical flow），一个输入的是appearance信息，输出的是分类结果。对于这样一个spatiotemporal的卷积网络，本文的处理方式是将一个随机初始化的input输入到两个flow中，然后针对某一个我们感兴趣，想要可视化的hidden layer计算feature map，计算出来之后，挑选一个channel c作为一个target feature channel，是我们最大化的对象，最大化的方式是通过改变input使得这个选出来的layer的feature map的channel c的激活最大化。改变input是通过将所有位置的target loss相加，对input求导，然后反向传播，和learning rate相乘，更新input的数值，一次次的迭代更新过程中，learning rate是在不断减小的，直到收敛停止训练，这个过程就像反向传播训练网络参数一样，只不过这次网络参数是固定的，但是input始终在变化，最终生成一个令人满意的input。

更加具体来讲，对于第l层网络的unit c（应该就是和之前一样指的channel c），我们想要寻找一个input ，其中H、W指的是图片的高度和宽度，T是temporal，C是color和optical flow的channel，也就是每一个像素对应的feature vector长度。优化的目标如下

这里面是第l层的activation，是对应第c个channel的自然基向量，应该就是一个one-hot的vector，除了第c个元素是1，其余全是0，是第l层的receptive field的大小（这里作者还加括号里面写了i.e. the input space，那可能指的是第l层经过层层叠加，receptive field不断扩大，在输入上所覆盖的receptive field大小，但是有点疑惑，这个为什么要作为规范项，每一层网络的输出如果是使用输出范围在0-1的那种激活函数，岂不是每一层的输出都在0-1之间，不需要scale，而若是使用了relu那种激活函数，其输入也是多个位置数值的加权求和，并不会随着网络层数加深而数值不断变大吧？），指的是在validation set上记录到的channel c的最大激活值，是一个regularization term（后面会介绍），前面还有一个权重λ。

接着作者介绍说，满足这个优化式子的input其实有很多，有一些和现实中的video其实是不符合的，也就是生成的input不真实（有点像gan的内容），因此需要加一些regularization进行限制，使得生成的input像素值的统计特征更接近真实。加入的regularization有两项，一个是用来限制input元素值的range的，也就是别出现离奇大的数值之类的不真实情况；第二个是用来增加smoothness的，为了使得生成的input元素值分布更接近真实的分布。

第一个称作regularizing local energy，用来压制过大的input数值，此regularizer记作，表达式如下

其中，ijk是spatiotemporal坐标，d指的是channel的坐标，可能是color的，也可能是motion的，B是限制数值的范围的，α是norm的指数。

第二个regularizer是用来限制frequency的，记作，用来防止input出现高频信息，因为真实的信号主要都是低频的。具体的表达式如下

是三个求偏导的算符，分别计算对spatiotemporal三个维度的导数值；是用来指定对spatial维度上进行多大的限制，指定对temporal维度上进行多大的限制，这个参数被称作slowness parameter，通过调整这个参数大小，可以调整让input的feature变化有多大的slowness，也就是说这个数值小了，那可能高频的信息也能存在，反之亦然。通过调整和控制spatial和temporalsmoothness的参数，可以有以下几个特殊情况：首先是只有spatial regularizer，即>0，=0，对temporal上的频率成分不做任何要求，这可以视作是加了一个2D的空域滤波器；第二个是isotropic spatiotemporal regularizer，且都大于0，对时空每一个维度都采取同样的限制，是一个3D时空域上的低通滤波器；第三个是各向异性的anisotropic spatiotemporal regularizer，≠，但是都大于零，这就增加了很多变数，例如可视化快速变化的feature，但同时又要在空域上光滑等等。这三种特殊的regularizer使得我们可以获得在空间上变化缓慢的input signal、时空维度上均匀变化的input signal和时空上变化不均的input signal。

有了这两个不同角度的regularizer，最终的总的regularizer就是两者相加，即

本文介绍的实验结果只有在UCF-101数据集上训练的VGG-16 two-stream fusion model（即上面的figure2），但是本文的可视化手段也可用于其他模型，作者在supplementary material中展示了更多的结果。

参照上面的Figure2，首先研究的是conv_5 fusion layer，这一层从两个flow获取信息，然后得到一个local fusion representation，输入到下一层全连接中，此层是整个网络中appearance和motion第一次合在一起，因此具有很大的研究价值，在这一层，同时发现了class specific的feature，也发现了class agnostic的更加general的feature。实验的思路是这样的，如下图所示

在此图中，可以猜测，这里面应该有一些filter会抓取例如“台球”这种概念来辅助分类，在conv_5中锁定这个对应着“台球”的unit的话，通过最大化这个unit的激活值，可以得到下图所示的结果

这些图是在spatial和temporal两个维度上加regularization和不加得到的input值，这个结果可以看出，这个unit可以对圆形的物体响应，并且变化快慢的时候是不一样的，作者借此认为这个unit是可以捕捉线性运动的物体。

通过类似的方法，可以研究全连接层之前的输入representation到底都抓取了一些什么特征，对应什么输入，是用来做什么的，对其它层也适用。