Singular Value Decomposition

---

向量矩阵可视化的 demo 可以参考 【python】Linear Algebra
对矩阵进行线性表示，类比泰勒公式！

---

1 特征分解（矩阵的基础概念）

1.1 相似矩阵

• 定义
  设 $A,B$ 都是 $n$ 阶矩阵，若存在可逆矩阵 $P$，使得 $P^{-1}AP=B$，则称 $A$ 相似于 $B$，记 $A$~$B$. 若 $A$~$\Lambda$，其中 $\Lambda$ 是对角矩阵，则称 $A$ 可相似对角化，$\Lambda$ 是 $A$ 的相似标准型。

• 相似矩阵的性质和矩阵可相似对角化的充要条件，这里不列举了！

1.2 正交矩阵

$A^{T}A=A{A}^T=I$ 的矩阵称为正交阵，其中 $I$ 为单位矩阵，也即$A^T=A^{-1}$

1.3 实对称矩阵

实对称矩阵，就是矩阵每个元素 $a_{ij}$ 都是实数，且 $A=A^T$

• 定理1：实对称矩阵的特征值全部是实数
• 定理2：实对称矩阵的属于不同特征值对应的特征向量相互正交
• 定理3：实对称矩阵必相似于对角阵（非对角元素都是 0 的矩阵），即存在可逆矩阵 $P$，使得 $P^{-1}AP=\Lambda$，且存在正交阵 $Q$，使得 $Q^{-1}AQ=Q^{T}AQ=\Lambda$（把 Q 甩过去就是矩阵的特征分解了）
  $A=(Q^T{)}^{{}_{-}1}\Lambda Q^{-1}=(Q^T{)}^T\Lambda Q^T=Q\Lambda Q^T$

1.4 特征值、特征向量

定义

$A$ 是 n 阶方阵，如果对于数 $\lambda$，存在非零向量 $v$，使得 $Av=\lambda v$，则称 $\lambda$ 是 $A$ 的特征值， $v$ 是 $A$ 对应于 $\lambda$ 的特征向量！

我们来升级一下 $Av=\lambda v$，变成如下形式（假设 A 有 n 个线性无关的特征向量）：

$$AV=\Lambda V$$

其中，$V=[v_1,v_2,...,v_n]$ 为特征向量（列向量）构成的矩阵。$\Lambda =[{\lambda }_1,{\lambda }_2,...,{\lambda }_n]$ 为特征值构成的对角矩阵。

再变形一下：

$$A=V\Lambda V^{-1}$$

如果 $A$ 是实对称矩阵，根据 1.3 中的定理2：实对称矩阵的属于不同特征值对应的特征向量相互正交，我们进一步变形下公式：

$$A=Q\Lambda Q^T$$

其中 $Q$ 是 $A$ 的特征向量组成的正交矩阵！

1.5 二次型

n 个变量的一个二次齐次多项式
$$f(x_1,x_2,...,x_n)=\sum _{i=1}^n\sum _{j=1}^n{a}_{ij}{x}_i{x}_j$$
称为 n 个变量的二次型，系数均为实数时，称为 n 元实二次型。矩阵表示为 $x^{T}Ax$，$A$ 是对称的矩阵，$x=[x_1,x_2,...,x_n{]}^T$。

$$[x_1,x_2,...,x_n]\left[\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right]$$

1.6 正定二次型和正定矩阵

若对于任意的非零向量 $x=[x_1,x_2,...,x_n{]}^T$，恒有 $f(x_1,x_2,...,x_n)=x^{T}Ax>0$，则称二次型 $f$ 为正定二次型，对应矩阵为正定矩阵。

$f(x_1,x_2,...,x_n)=x^{T}Ax$ 正定，有许多等价的表示，其中一条就是 A 的全部特征值 ${\lambda }_i>0$

1.7 特征分解

本质：原矩阵（方阵）分解成了许多方阵的线性组合（类比泰勒公式）！

对称矩阵一定能特征分解（特别是对称正定矩阵，能保证 ${\lambda }_i$ 都是正数）

$$A=Q\Lambda Q^T$$

设 $Q$ 为 $[v_1,v_2,...,v_n]$，其中 $v_i\in {\mathbb{R}}^n$，表示 $A$ 的特征向量！

$\Lambda =\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & ...& \\ & & & {\lambda }_n\end{array}\right)$，其中 ${\lambda }_i$ 为特征向量 $v_i$ 对应的特征值。

则
$$\begin{array}{rl}A& =[v_1,v_2,...,v_n]\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & ...& \\ & & & {\lambda }_n\end{array}\right)\left(\begin{array}{c}{v}_1^T\\ v_2^T\\ ...\\ v_n^T\end{array}\right)\\ & ={\lambda }_1{v}_1{v}_1^T+{\lambda }_2{v}_2{v}_2^T+...+{\lambda }_n{v}_n{v}_n^T\end{array}$$

分解得到的这些方阵有什么特点呢？是由一个列向量（$n\times 1$）和一个行向量（$1\times n$）相乘得到的，原来的 $n\times n$ 矩阵 A 参数量 $n^2$，特征分解后，参数量最多可以达到 $(n\times 1+1)\times n=n^2+n$（1 表示的是 ${\lambda }_i$，哈哈，参数量变多了）

但是我们可以选取特征值 ${\lambda }_i$ 较大的方阵，表示对最后的结果贡献越高！这样一来，参数量大大的减少了（最少 $n\times 1+1$，仅仅保留一项） ，达到了压缩的目的！

2 SVD 分解

2.1 推导

SVD，singular value decomposition，奇异值分解

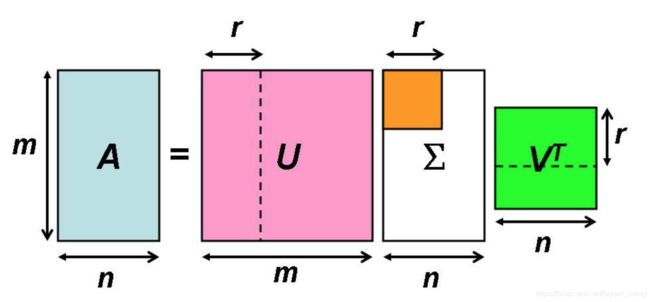
r 是矩阵 A 的秩

图片来源：http://www.imooc.com/article/267351

---

本质：原矩阵（不限于方阵）分解成了许多矩阵的线性组合（类比泰勒公式）！

这里比矩阵的特征分解更进一步，不再要求是方阵了，更有普适性了。具体转化过程如下：

虽然 $A_{m\times n}$ 不是方阵 ，但是 $A{A}_{m\times m}^T$ 和 $A^T{A}_{n\times n}$ 组成 CP 后，就是方阵了。我们假设：

$$(A{A}^T{)}_{m\times m}=U{\Lambda }^2{U}^T$$

$$(A^{T}A{)}_{n\times n}=V{\Lambda }^2{V}^T$$

${\Lambda }_{m\times n}^2$ 是 $A{A}^T$ 和 $A^{T}A$ 的特征值（$AB$ 和 $BA$ 的特征值是一样的，非零）

$U_{m\times m}=(u_1,u_2,...,u_m)$， $U$ 为正交矩阵

$V_{n\times n}=(v_1,v_2,...,v_n)$，$V$ 为正交矩阵

可以得到 $A$ 的形式如下

$$A_{m\times n}=U\Lambda V^T={\lambda }_1^{\frac{1}{2}}{u}_1{v}_1^T+{\lambda }_2^{\frac{1}{2}}{u}_2{v}_2^T+...$$

加法的最后一项根据 $m,n$ 中较小的一项决定

$u_1$ 是 $m\times 1$，$v_1$ 是 $n\times 1$，图像压缩存储时最少需要 $m+n+1$

图片来自于 deepshare.net

1）$A_{m\times n}$ 为什么是 $U\Lambda V^T$ 这种形式呢？

反推一下，假设已知

$$A=U\Lambda V^T$$

转置一下

$$A^T=V{\Lambda }^T{U}^T$$

组合一下

$$A{A}^T=U\Lambda V^{T}V{\Lambda }^T{U}^T=U\Lambda {\Lambda }^T{U}^T=U{\Lambda }^2{U}^T$$

$$A^{T}A=V{\Lambda }^T{U}^{T}U\Lambda V^T=V{\Lambda }^T\Lambda V^T=V{\Lambda }^2{V}^T$$

OK，形式没错

2）U 和 V 的关系是什么

$$A=U\Lambda V^T$$

左右同时乘以 $V$

$$AV=U\Lambda V^{T}V=U\Lambda$$

所以

$$U=\frac{AV}{\Lambda }$$

其中，${\Lambda }_{m\times n}^2$ 是由 ${\lambda }_1$,${\lambda }_2$ …构成的对角矩阵，细节一点可以写成如下形式：

$$u_i=\frac{A{v}_i}{\sqrt{{\lambda }_i}}$$

3）$A_{m\times n}$ 的具体推导过程

对于矩阵 $A^T{A}_{n\times n}$，有 $A^{T}A{v}_i={\lambda }_i{v}_i$，设 ${\lambda }_i$ 为 $A^{T}A$ 的特征值，$v_i$ 为对应的特征向量。前面我们令 $U$ 和 $V$ 为正交矩阵，所以 $v_i^T{v}_j=0$。

进一步分析：
$$\begin{array}{rl}(A{v}_i{)}^{T}A{v}_j& =v_i^T{A}^{T}A{v}_j\\ & =v_i^T{\lambda }_j{v}_j\\ & ={\lambda }_j{v}_i^T{v}_j=0\end{array}$$

所以 $A{v}_i$ 与 $A{v}_j$ 也是正交的，同理 $(A{v}_i{)}^{T}A{v}_i$ 可以进行如下化简：

$$\begin{array}{rl}(A{v}_i{)}^{T}A{v}_i& =v_i^T{A}^{T}A{v}_i\\ & =v_i^T{\lambda }_i{v}_i\\ & ={\lambda }_i{v}_i^T{v}_i={\lambda }_i\end{array}$$

也即

$$|A{v}_i{|}^2={\lambda }_i$$，$$|A{v}_i|=\sqrt{{\lambda }_i}$$

因此

$$\frac{A{v}_i}{|A{v}_i|}=\frac{1}{\sqrt{{\lambda }_i}}A{v}_i$$

前面我们已经知道

$$u_i=\frac{1}{\sqrt{{\lambda }_i}}A{v}_i$$

因此

$$A{v}_i=|A{v}_i|u_i=\sqrt{{\lambda }_i}{u}_i$$

写成矩阵的形式，如下所示：
$$\begin{array}{rl}AV& =A(v_1,v_2,...,v_n)\\ & =(A{v}_1,A{v}_2,...,A{v}_n)\\ & =(\sqrt{{\lambda }_1}{u}_1,\sqrt{{\lambda }_2}{u}_2,...,\sqrt{{\lambda }_n}{u}_n)\\ & =\Lambda U=U\Lambda \end{array}$$

因此

$$A=U\Lambda V^{-1}=U\Lambda V^T$$

举个小例子：

比如，打开图片，开始先模糊，后面越来越清晰，本质就是，先传重要的信息（比如 SVD 中特征值比较大的分量），再补细节信息！

2.2 计算一个矩阵的 SVD 形式

$$A=\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$$

1）计算 $A{A}_{3\times 3}^T$ 的特征值和特征向量

$$A{A}_{3\times 3}^T=\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right)=\left(\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$$

$$|\lambda E-A{A}^T|=\left|\begin{array}{ccc}\lambda -1& -1& 0\\ -1& \lambda -2& -1\\ 0& -1& \lambda -1\end{array}\right|=\lambda (\lambda -3)(\lambda -1)$$

所以 ${\lambda }_1=3$， ${\lambda }_2=1$， ${\lambda }_3=0$

i) 当 $\lambda =3$ 时

$$(\lambda E-A{A}^T)X=0$$

矩阵为
$$\left(\begin{array}{ccc}2& -1& 0\\ -1& 1& -1\\ 0& -1& 2\end{array}\right)\Rightarrow \left(\begin{array}{ccc}1& 0& -1\\ 0& 1& -2\\ 0& 0& 0\end{array}\right)$$

对应的单位化的特征向量 $u_1$ 为 $$(\frac{1}{\sqrt{6}},\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}}{)}^T$$

ii) 当 $\lambda =1$ 时

$$(\lambda E-A{A}^T)X=0$$

矩阵为

$$\left(\begin{array}{ccc}0& -1& 0\\ -1& -1& -1\\ 0& -1& 0\end{array}\right)\Rightarrow \left(\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)$$

对应的单位化的特征向量 $u_2$ 为 $$(\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}}{)}^T$$

iii) 当 $\lambda =0$ 时

$$(\lambda E-A{A}^T)X=0$$

矩阵为

$$\left(\begin{array}{ccc}-1& -1& 0\\ -1& -2& -1\\ 0& -1& -1\end{array}\right)\Rightarrow \left(\begin{array}{ccc}1& 0& -1\\ 0& 1& 1\\ 0& 0& 0\end{array}\right)$$

对应的单位化的特征向量 $u_3$ 为 $$(\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}{)}^T$$

综上所述：

$$A{A}^T=U{\Lambda }^2{U}^T=\left(\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\\ \frac{2}{\sqrt{6}}& 0& -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\end{array}\right)\left(\begin{array}{ccc}3& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{2}{\sqrt{6}}& \frac{1}{\sqrt{6}}\\ \frac{1}{\sqrt{2}}& 0& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{3}}& -\frac{1}{\sqrt{3}}& \frac{1}{\sqrt{3}}\end{array}\right)$$

2）计算 $A^T{A}_{2\times 2}$ 的特征值和特征向量

$$A^T{A}_{2\times 2}=\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right)\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}2& 1\\ 1& 2\end{array}\right)$$

$$|\lambda E-A^{T}A|=\left|\begin{array}{cc}\lambda -2& -1\\ -1& \lambda -2\end{array}\right|=(\lambda -3)(\lambda -1)$$

所以 ${\lambda }_1=3$， ${\lambda }_2=1$

i) 当 $\lambda =3$ 时

$$(\lambda E-A^{T}A)X=0$$

矩阵为

$$\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}1& -1\\ 0& 0\end{array}\right)$$

对应的单位化的特征向量 $v_1$ 为 $$(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}{)}^T$$

ii) 当 $\lambda =1$ 时

$$(\lambda E-A^{T}A)X=0$$

矩阵为

$$\left(\begin{array}{cc}-1& -1\\ -1& -1\end{array}\right)\Rightarrow \left(\begin{array}{cc}1& 1\\ 0& 0\end{array}\right)$$

对应的单位化的特征向量 $v_2$ 为 $$(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}{)}^T$$

---

PS：这里有点小疑惑，如果 $v_2$ 按照上面的格式写，最终通过 $U$ 和 $V$ 计算 $A$ 的时候第一列和第二列位置互换了，需要写成 $v_2$ 为 $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}{)}^T$，这两种结果在计算特征值的时候是等价的！

感觉应该需要用 $u_i$ 和 $v_i$ 的关系约束下：

前面我们已知
$$u_i=\frac{1}{\sqrt{{\lambda }_i}}A{v}_i$$

这里带进去看看

$$u_2=\frac{1}{\sqrt{{\lambda }_2}}A{v}_2$$

$$\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ 0\\ -\frac{1}{\sqrt{2}}\end{array}\right)=\frac{1}{\sqrt{1}}\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$$

确实 $v_2$ 为 $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}{)}^T$ 而不是 $(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}{)}^T$

---

回归正题，综上所述：

$$A^{T}A=V{\Lambda }^2{V}^T=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{cc}3& 0\\ 0& 1\end{array}\right)\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)$$

所以

$$A=U\Lambda V^T=\left(\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\\ \frac{2}{\sqrt{6}}& 0& -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\end{array}\right)\left(\begin{array}{cc}\sqrt{3}& 0\\ 0& 1\\ 0& 0\end{array}\right)\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$$

3 逆矩阵（以最小二乘为例）

定义：
设 $A$ 是 $n$ 阶矩阵，如果存在 $n$ 阶矩阵 $B$ 使得

$$AB=E(单位矩阵)$$

成立，则称 $A$ 是可逆矩阵，$B$ 是 $A$ 的逆矩阵，记成 $A^{-1}=B$.

可逆矩阵有两个非常重要的性质：

• $|A|̸=0$，或者秩 $r(A)=n$，或 $A$ 的列（行）向量无关；
• 矩阵 $A$ 的特征值全不为 0

---

下面以最小二乘为例，分析下逆矩阵和伪逆矩阵，假设有 $N$ 个样本，每个样本 $n$ 维
$$x_1,x_2,...,x_N,x_i\in {\mathbb{R}}^n$$

$N$ 个标签，每个标签 $1$ 维

$$y_1,y_2,...,y_N,y_i\in {\mathbb{R}}^1$$

我们需要求解的就是 $x\to y$ 的关系，形象化一点

$$\{\begin{array}{c}{y}_1=x_1^1{a}_1+x_1^2{a}_2+...+x_1^n{a}_n\\ y_2=x_2^1{a}_1+x_2^2{a}_2+...+x_2^n{a}_n\\ ...\\ y_N=x_N^1{a}_1+x_N^2{a}_2+...+x_N^n{a}_n\end{array}$$

其中 $x_i^j$ 表示第 $i$ 个样本的第 $j$ 维！

写成矩阵的形式：

$${\left(\begin{array}{cccc}{x}_1^1& x_1^2& ...& x_1^n\\ x_2^1& x_2^2& ...& x_2^n\\ ...& ...& ...& ...\\ x_N^1& x_N^2& ...& x_N^n\end{array}\right)}_{N\times n}{\left(\begin{array}{c}{a}_1\\ a_2\\ ...\\ a_n\end{array}\right)}_{n\times 1}={\left(\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_N\end{array}\right)}_{N\times 1}$$

也即

$$X_{N\times n}{a}_{n\times 1}=Y_{N\times 1}$$

问题的关键就是求出来 $a_{n\times 1}$ 了！我们已知 $X$ 和 $Y$，所以，当 $N=n$ 且 $X_{N\times n}$ 可逆时：
$$a=X^{-1}Y$$

4 伪逆矩阵（以最小二乘为例）

一般情况下，样本总个数 $N$ 和每个样本的维数 $n$ 是不相等的，这个时候 $X$ 显然不可逆（连方阵都不是），$a=X^{-1}Y$ 的求法行不通！

怎么破？

我们可以用 $Xa$ 来逼近 $Y$，也即最小化 $J$

$$J=||Xa-Y|{|}^2$$

未知数是 $a$，对 $a$ 求偏导，令导数为零求极值

$$\frac{\partial J}{\partial a}=2X^T(Xa-Y)=0$$

化简一下：

$$X^{T}Xa=X^{T}Y$$

问题就转换为了 $X^{T}X$ 是否可逆！

1）如果 $N>n$

$(X^{T}X{)}_{n\times n}$ 一般是可逆的，此时：

$$a=(X^{T}X{)}^{-1}{X}^{T}Y$$

如果 $X$ 可逆的话，把可逆符号作用在括号里

$$a=X^{-1}(X^T{)}^{-1}{X}^{T}Y=X^{-1}Y$$

和上一节的结论一致，所以 $a=(X^{T}X{)}^{-1}{X}^{T}Y$ 叫做伪逆矩阵的形式！是一种更普适性的解法。

通过 $a=X^{-1}(X^T{)}^{-1}{X}^{T}Y=X^{-1}Y$ 给出解的系统方程被称为正规方程（normal equation）.

2）如果 $N<n$

样本的个数小于样本的维度，也就是样本的表示太复杂了，过拟合的节奏！

$(X^{T}X{)}_{N\times N}$

我们已知秩的如下性质：
$$r(AB)\le min(r(A),r(B))$$

所以
$$r(X^{T}X)\le r(X)\le n$$

所以
$$r(X^{T}X)̸=N$$

根据逆矩阵的性质可知，$X^{T}X$ 不可逆，也即伪逆 $a=X^{-1}(X^T{)}^{-1}{X}^{T}Y$ 的路也行不通了，怎么破！

此时我们要用到最小范数解，也就是我们熟悉的加正则项（regularization）

5 最小范数解（以最小二乘为例）

此时 $J$ 引入了正则项

$$J=||Xa-Y|{|}^2+\lambda ||a|{|}^2$$

对 $a$ 计算偏导，令其为 0，来求极值：

$$\frac{\partial J}{\partial a}=2X^T(Xa-Y)+2\lambda a=0$$

化简一下（因为$X^{T}X$ 是方阵，所以引入了单位矩阵 $I$）：

$$(X^{T}X+\lambda I)a=X^{T}Y$$

问题聚焦到 $X^{T}X+\lambda I$ 是否可逆！

我们已知 $X^{T}X$ 是实对称矩阵，所以 $X^{T}X$ 一定可以相似对角化（特征值，可以参考实对称矩阵小节中的定理3），转换一下形式，可以写成：

$$X^{T}X=Q\left(\begin{array}{ccc}{\lambda }_1& & \\ & ...& \\ & & {\lambda }_n\end{array}\right)Q^T$$

行列式为特征值的乘积

$$|X^{T}X|={\lambda }_1{\lambda }_2...{\lambda }_n$$

给定一个非零向量 $m$，把矩阵 $X^{T}X$ 写成二次型的形式：

$$m^T{X}^{T}Xm=(Xm{)}^T(Xm)\ge 0\to {\lambda }_i\ge 0$$

只能保证是半正定，$|X^{T}X|$ 还是有可能为0，也即无法保证 $X^{T}X$ 可逆（前面已经证明了$X^{T}X$ 不可逆，这里仅从表达式入手），引入正则项以后情况就不一样了。

---

$X^{T}X+\lambda I$ 同样也是实对称矩阵，因为只是在对角线上有改动，同样的可以写成

$$X^{T}X+\lambda I=Q\left(\begin{array}{ccc}{\lambda }_1& & \\ & ...& \\ & & {\lambda }_n\end{array}\right)Q^T$$

给定一个非零向量 $m$，把矩阵 $X^{T}X+\lambda I$ 写成二次型的形式：

$$m^T(X^{T}X+\lambda I)m=(Xm{)}^T(Xm)+\lambda m^{T}m>0\to {\lambda }_i>0$$

这么一来，$X^{T}X+\lambda I$ 就是正定矩阵了，就能保证对应的特征值全部大于0，也即 $|X^{T}X+\lambda I|={\lambda }_1{\lambda }_2...{\lambda }_n>0$，结合矩阵可逆的条件，可以得出，矩阵 $X^{T}X+\lambda I$ 是可逆矩阵！

所以 $a$ 可以表示为：

$$a=(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y$$

补充（参考 https://blog.csdn.net/asd136912/article/details/79146151）

---

综合 3，4，5 小节，已知

$$X_{N\times n}{a}_{n\times 1}=Y_{N\times 1}$$

可以得出：
$$a=\{\begin{array}{c}\begin{array}{rlr}& X^{-1}Y，& 如果N=n，且X可逆\\ & (X^{T}X{)}^{-1}{X}^{T}Y，& 如果N>n（伪逆）\\ & (X^{T}X+\lambda I{)}^{-1}{X}^{T}Y，& 如果N<n（最小范数解）\end{array}\end{array}$$